Đề thi thử tốt nghiệp THPT 2025 môn Toán Sở GD&ĐT Bình Dương
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2024 - 2025
BÌNH DƯƠNG Môn: TOÁN, Lớp 12
MÃ ĐỀ 4110 Thời gian: 90 phút, không kể thời gian phát đề
Đề thi có 04 trang
Họ, tên thí sinh: .................................................................. Số báo danh: .................................
PHẦN I (3,0 điểm). Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu
12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trong không gian Oxyz, cho đường thẳng d :
x − 2
−3
=
y + 5
2
=
z − 2
−2
. Vectơ nào dưới đây là một
vectơ chỉ phương của d?
A.
−→
u
4
= (−3; 2; 2). B.
−→
u
1
= (2; −5; 2). C.
−→
u
3
= (2; 5; −2). D.
−→
u
2
= (3; −2; 2).
Câu 2. Nguyên hàm của hàm số f(x) =
1
x
+ x là
A. ln |x| +
1
2
x
2
+ C. B. ln |x| + x
2
+ C. C. ln x +
1
2
x
2
+ C. D. ln x + x
2
+ C.
Câu 3. Một lớp học có 20 học sinh nam và 25 học sinh nữ. Tổng kết cuối năm học, lớp có 12 học sinh nữ
đạt danh hiệu học sinh xuất sắc. Chọn ngẫu nhiên một học sinh của lớp. Tính xác suất để học sinh được
chọn là học sinh xuất sắc, biết học sinh đó là nữ.
A. 30%. B. 48%. C. 50%. D. 60%.
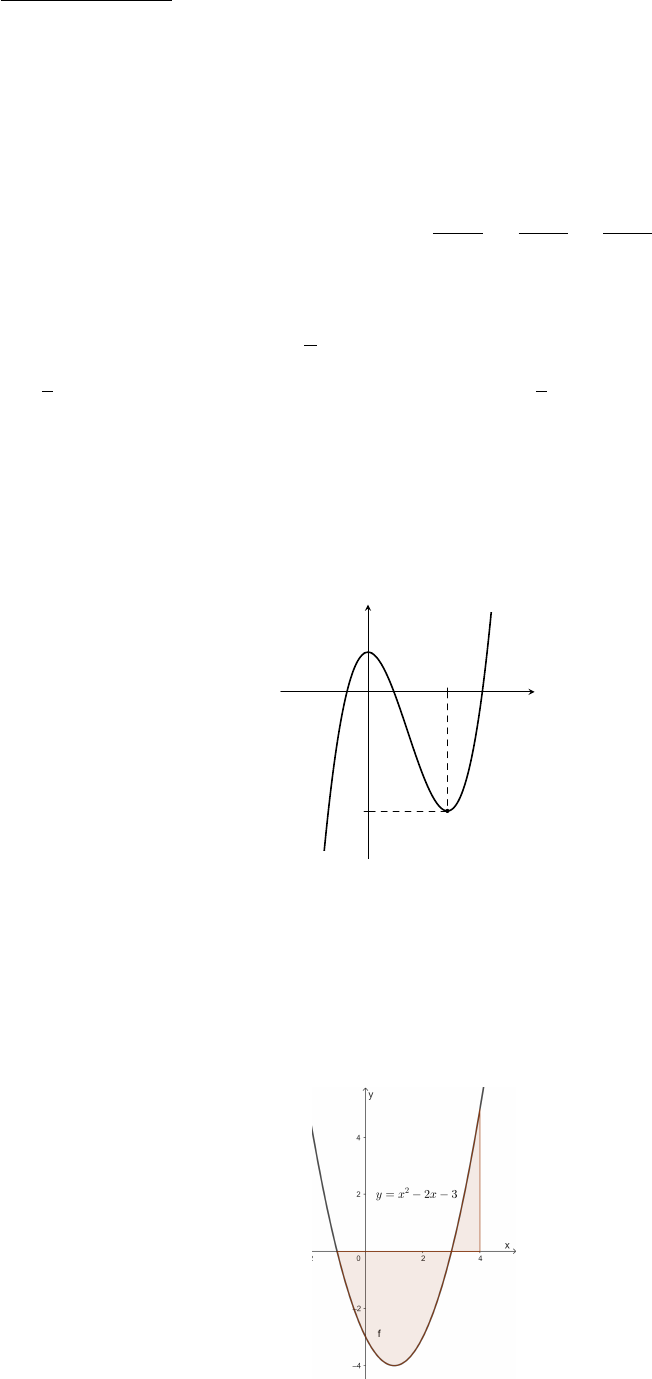
Câu 4. Cho hàm số y = f(x) có đồ thị là đường cong trong hình bên.
x
y
O
2
−3
1
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (0; 2). B. (2; +∞). C. (−3; 1). D. (−∞; 0).
Câu 5. Tập nghiệm của bất phương trình 4
x+1
≤ 16 là
A. ∅. B. [1; +∞). C. (0; 1). D. (−∞; 1].
Câu 6. Cho hình phẳng (H) được giới hạn bởi các đường y = x
2
−2x −3, y = 0, x = −1, x = 4 (như hình
minh họa).
Diện tích của hình phẳng (H) là
A. 13. B. 12. C. 8, 3. D. 11.
1
Câu 7. Phương trình nào sau đây là phương trình mặt phẳng (Oyz)?
A. x = 0. B. z = 0. C. y = 0. D. x + y = 0.
Câu 8. Cho f (x) liên tục trên [−1; 3]. Biết F (x) là một nguyên hàm của f(x) trên [−1; 3] thỏa F (−1) = 3,
F (3) = 7. Khi đó
3
Z
−1
f(x) dx bằng
A. 4. B. 10. C. −6. D. −2.
Câu 9. Đồ thị của hàm số y =
x + 1
2x − 3
có đường tiệm cận đứng là
A. x = −
3
2
. B. x =
3
2
. C. x = −1. D. x =
1
2
.
Câu 10. Phương sai của một mẫu số liệu ghép nhóm cho bởi bảng thống kê bên dưới gần nhất với giá trị
nào sau đây?
Lớp chiều cao [150; 154) [154; 158) [158; 162) [162; 166) [166; 170)
Tần số 25 50 200 175 50
Giá trị đại diện 152 156 160 164 168
A. 14, 84. B. 18, 84. C. 15, 74. D. 13, 24.
Câu 11. Trong không gian Oxyz, cho điểm A(0; −3; 2) và mặt phẳng (P ) : 2x −y + 3z + 5 = 0. Mặt phẳng
đi qua A và song song với (P ) có phương trình là
A. 2x + y + 3z + 3 = 0. B. 2x − y + 3z − 9 = 0.
C. 2x − y + 3z + 9 = 0. D. 2x + y + 3z − 3 = 0.
Câu 12. Cho cấp số nhân (u
n
) có u
2
= 3, u
3
= 6. Công bội q của cấp số nhân là
A. 6. B. 3. C. 2. D. 4.
PHẦN II (4,0 điểm). Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d)
ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
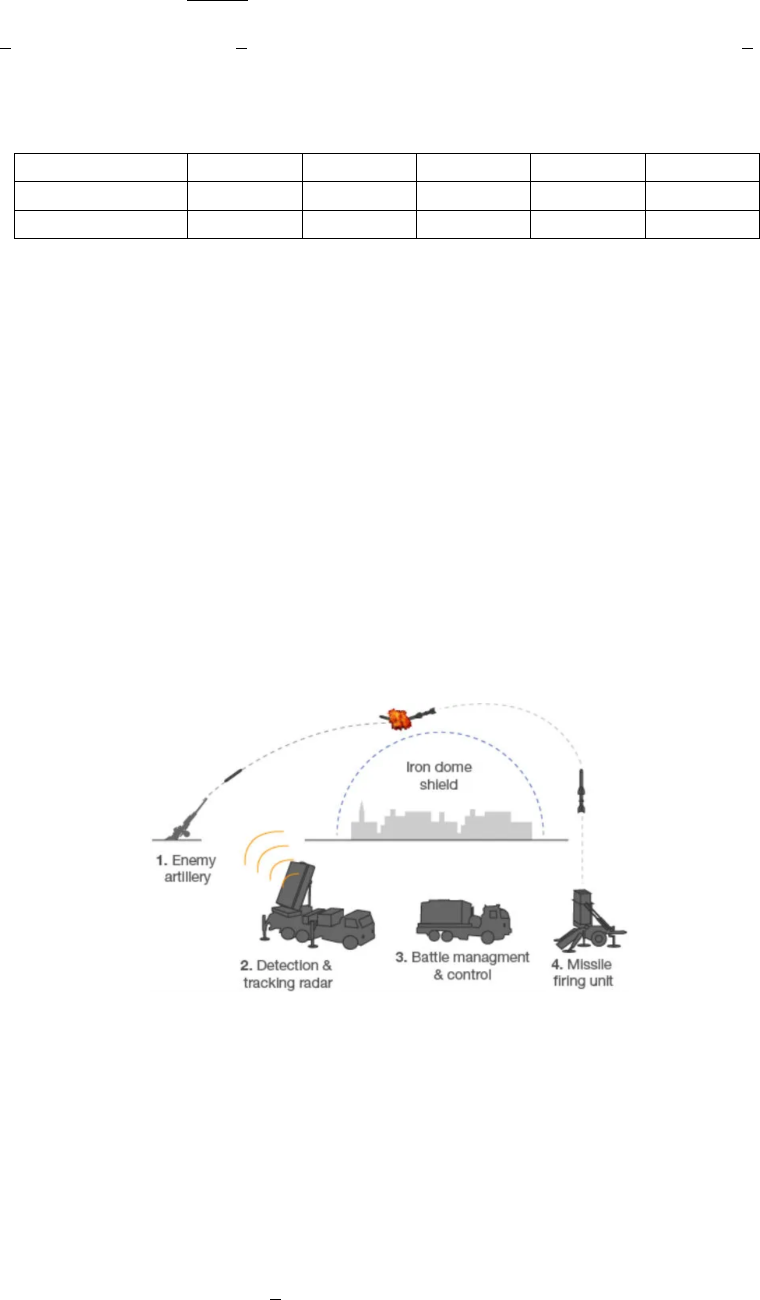
Câu 1. Hệ thống phòng không “Vòm sắt” là một trong những hệ thống đánh chặn tên lửa từ xa rất nổi
tiếng của Israel. Để “Vòm sắt” hoạt động được chính xác, người ta trang bị một Radar có khả năng phát
hiện tên lửa với bán kính 417 km. Trong hệ trục tọa độ Oxyz, một hệ thống “Vòm sắt” đang ở vị trí O(0; 0; 0)
và một quả tên lửa đang ở vị trí A(688; 185; −8) được phóng lên và bay theo một quỹ đạo là đường thẳng
có vectơ chỉ phương là
−→
u = (−91; −75; 0).
Trong các mệnh đề sau, mệnh đề nào đúng, mệnh đề nào sai? (hình vẽ chỉ mang tính chất minh họa)
a) Phương trình mặt cầu thể hiện vùng phủ sóng của Radar là x
2
+ y
2
+ z
2
= 417
2
.
b) Radar phát hiện một quả tên lửa ngay tại vị trí được phóng lên.
c) Giả sử hệ thống “Vòm sắt” gặp trục trặc không thể bắn hạ quả tên lửa, khi đó vị trí cuối cùng quả
tên lửa xuất hiện trên màn hình radar là B(−40; −415; −8).
d) Nếu hệ thống gặp trục trặc không bắn hạ được tên lửa thì khoảng cách gần nhất từ hệ thống “Vòm
sắt” đến quả tên lửa là ≈ 295 km.
Câu 2. Cho hàm số f (x) = 2 cos x + x
√
2.
2

a) Tính f(0) = 2 và f (π) = −2 + π
√
2.
b) Đạo hàm của hàm số đã cho là f
′
(x) = 2 sin x +
√
2.
c) Phương trình f
′
(x) = 0 có đúng 2 nghiệm trên đoạn [0; π].
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của f (x) trên đoạn [0; π] là π
√
2.
Câu 3. Trên đường quốc lộ, một ô tô đang di chuyển với vận tốc 12, 5 m/s. Cùng lúc, một đoàn tàu chạy
cùng hướng và song song với đường quốc lộ với vận tốc
50
3
m/s. Khi ô tô cách đuôi tàu 100 mét thì ô tô bắt
đầu tăng tốc với vận tốc v(t) = 2, 5t + b (m/s), với t là thời gian kể từ lúc ô tô bắt đầu tăng tốc. Khi ô tô
đạt đến vận tốc tối đa cho phép 25 m/s thì ô tô giữ nguyên vận tốc.
a) Giá trị của b bằng 12, 5.
b) Thời gian ô tô đạt vận tốc tối đa cho phép là 5 giây.
c) Sau 5 giây kể từ khi ô tô tăng tốc, ô tô đi được quãng đường nhỏ hơn quãng đường của tàu đi được.
d) Thời gian ô tô bắt kịp đuôi tàu kể từ lúc ô tô bắt đầu tăng tốc là 15, 75 giây.
Câu 4. Khi điều tra sức khỏe nhiều người cao tuổi ở một địa phương, người ta thấy rằng có 40% người cao
tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những người bị bệnh tiểu đường
là 70%, trong những người không bị bệnh tiểu đường là 25%. Chọn ngẫu nhiên 1 người cao tuổi để kiểm tra
sức khỏe.
a) Xác suất chọn được người bị bệnh tiểu đường là 0, 4.
b) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó bị bệnh tiểu đường, là 0, 7.
c) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó không bị bệnh tiểu đường, là 0, 75.
d) Xác suất chọn được người bị bệnh huyết áp cao là 0, 8.
PHẦN III (3,0 điểm). Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Một tòa nhà có hình dạng là một hình chóp tứ giác đều có cạnh đáy là 160 m và cạnh bên là 140 m.
Giả sử, từ một mặt bên của tòa nhà ta cần thiết kế con đường ngắn nhất để đi chuyển đến tâm của đáy tòa
nhà, khi đó quãng đường ngắn nhất có độ dài khoảng bao nhiêu mét? (làm tròn đến hàng chục)
Câu 2. Nhà máy A chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy B. Hai nhà máy thỏa thuận,
mỗi tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu
số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là P (x) = 45 −0, 001x
2
(triệu đồng).
Chi phí để A sản xuất x tấn sản phẩm trong một tháng là C(x) = 100 + 30x (triệu đồng) (gồm 100 triệu
đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm). Để mỗi tháng thu được lợi nhuận lớn nhất
thì A cần bán cho B khoảng bao nhiêu tấn sản phẩm? (kết quả làm tròn đến hàng đơn vị)
3
Đề thi thử tốt nghiệp môn Toán Sở Bình Dương
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán Sở GD&ĐT Bình Dương được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Mời các bạn cùng theo dõi đề thi dưới đây để có thêm tài liệu ôn thi kì Thi THPT Quốc gia sắp tới nhé.


