VnDoc.com

Đề thi thử tốt nghiệp THPT 2025 môn Toán lần 1 Sở GD&ĐT Bắc Giang

Thi THPT Quốc gia 2025

Tải về

Lớp: THPT Quốc gia

Môn: Toán

Dạng tài liệu: Đề thi

Loại: Tài liệu Lẻ

Loại File: PDF

Phân loại: Tài liệu Tính phí

1/4 - Mã đề 101

SỞ GIÁO DỤC VÀ ĐÀO TẠO

BẮC GIANG

(Đề thi có 04 trang)

ĐỀ THI THỬ TỐT NGHIỆP THPT (lần 1)

NĂM HỌC 2024 - 2025

MÔN: TOÁN

Th

ời gian l

àm bài 90 phút; không k

ể thời gian phát đề

- Họ và tên thí sinh:…………………………………………

- Số báo danh:……………………………………………….

PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Nghiệm của phương trình

2

log 3

x



là

A.

5

x



. B.

8

x



. C.

6

x



. D.

9

x



.

Câu 2. Trong không gian

Oxyz

, cho vectơ

2 5

u i k

 

  

. Tọa độ của vectơ

u



là

A.





0; 2; 5



. B.





2; 0; 5

. C.





2; 5; 0



. D.





2; 0; 5



.

Câu 3. Trong không gian

Oxyz

, cho hai điểm





1; 2; 1

A 

và





2; 1; 3

B



. Tọa độ của vectơ

AB



là

A.

1 3

; ; 1

2 2

 



 

 

. B.





3; 1; 4



. C.





3; 1; 4

 

. D.





1; 3; 2



.

Câu 4. Nguyên hàm của hàm số





sin

f x x



là

A.

cos

x C



. B.

2

sin

2

x

C



. C.

cos

x C

 

. D.

sin

x C



.

Câu 5. Giá trị nhỏ nhất của hàm số

4 2

4 3

y x x

  

trên đoạn





0; 4

là

A.

0

. B.

2

. C.

3

. D.

1



.

Câu 6. Một hộp đựng 9 tấm thẻ cùng loại được ghi số từ 1 đến 9. Rút ngẫu nhiên đồng thời hai tấm thẻ từ

trong hộp. Xác suất để rút được cả hai tấm thẻ cùng ghi số chẵn là

A.

1

2

. B.

1

3

. C.

5

6

. D.

1

6

.

Câu 7. Cấp số nhân





n

u

có

1

2

u



và

2

6

u



. Số hạng

4

u

của cấp số nhân là

A. 27. B. 162. C. 54. D. 11.

Câu 8. Tập nghiệm của bất phương trình









1 1

2 2

log 1 log 2 1

x x

  

là

A.

1

; 2

2

 





 

. B.

1

; 2

2

 

 

 

. C.





; 2



. D.





; 2



.

Câu 9. Thể tích của khối chóp có diện tích đáy bằng

S

, chiều cao bằng

h

là

A.

1

.

2

V S h



. B.

1

.

3

V S h



. C.

.

V S h



. D.

2

.

3

V S h



.

Câu 10. Cho hàm số





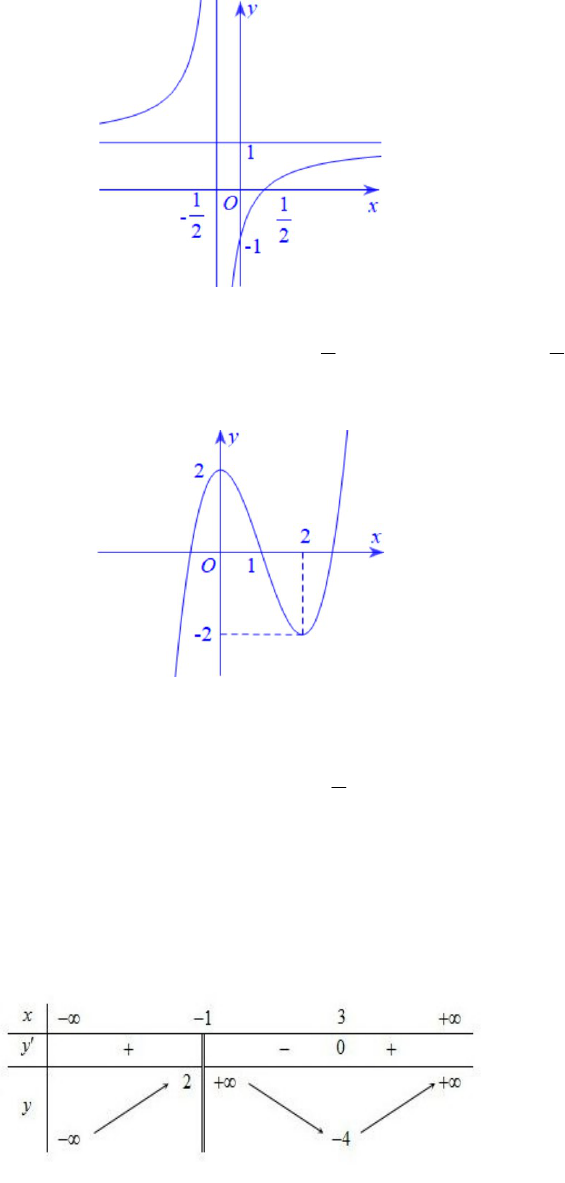
y f x



có đồ thị như hình vẽ dưới đây:

Mã đề 101

2/4 - Mã đề 101

Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình

A.

1

x



. B.

1

y



. C.

1

2

x

 

. D.

1

2

y

 

.

Câu 11. Cho hàm số





y f x



có đồ thị như hình vẽ dưới đây:

Hàm số đã cho đồng biến trên khoảng

A.





2;

 

. B.





0; 2

. C.





1;

 

. D.





; 1

 .

Câu 12. Gọi





F x

là một nguyên hàm của hàm số

 

1

2f x x

x

 

thỏa mãn





1 1

F



. Tính





1

F



.

A.





1 1

F

 

. B.





1 2

F

 

. C.





1 1

F

  

. D.





1 0

F

 

.

PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số





y f x



có bảng biến thiên như sau:

a) Đồ thị hàm số





y f x



có đúng hai đường tiệm cận.

b) Hàm số





y f x

 đồng biến trên





3;



.

c) Hàm số





y f x



có đúng một điểm cực trị.

d) Giá trị nhỏ nhất của









2 2025

h x f x x

  trên đoạn





3;2025

bằng

6083

.

Câu 2. Trong không gian

Oxyz

, cho ba điểm

(2; 1;1)

A



,

( 1;3; 1)

B

 

,

(5; 3;4)

C



.

3/4 - Mã đề 101

a) Tích vô hướng của hai vectơ

AB



và

AC



bằng

23.



b) Góc



BAC

là góc nhọn.

c) Côsin của góc giữa hai vectơ

AB



,

AC



bằng

23

638



.

d) Lấy điểm M trên mặt phẳng

Oxy

sao cho biểu thức

2 2 2

MA MB MC

  đạt giá trị nhỏ nhất. Khi đó tọa độ

của M là

1

2; ;0

3



 

 

 

.

Câu 3. Xét phương trình

2sin 3 1 0

x

 

.

a) Tập nghiệm của phương trình là

2 5 2

;

18 3 18 3

k k

S k

   

 

   

 

 



.

b) Nghiệm dương nhỏ nhất của phương trình là

18

x





.

c) Phương trình có đúng 3 nghiệm trên





0;



.

d) Tổng các nghiệm của phương trình thuộc đoạn





0;



bằng

2



.

Câu 4. Cho hàm số

 

2 1

x

f x

x





.

a)

( ) 2 ln

f x dx x x C

  



.

b) Gọi





F x

là một nguyên hàm của hàm số





f x

và thỏa mãn





1 3

F



. Khi đó





2 ln 1.

F x x x

  

c)

1

'(2 )

4

f x dx C

x



 



.

d) Gọi





G x

là một nguyên hàm của hàm số





f x

. Biết





2 1

G



và









5 5 0

G G

  

. Khi đó tìm được





10 ln10 ln5 ln 2

G a b c d

    

, với

, ,

a b c

là các số hữu tỷ. Khi đó

19

a b c d

    

.

PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.

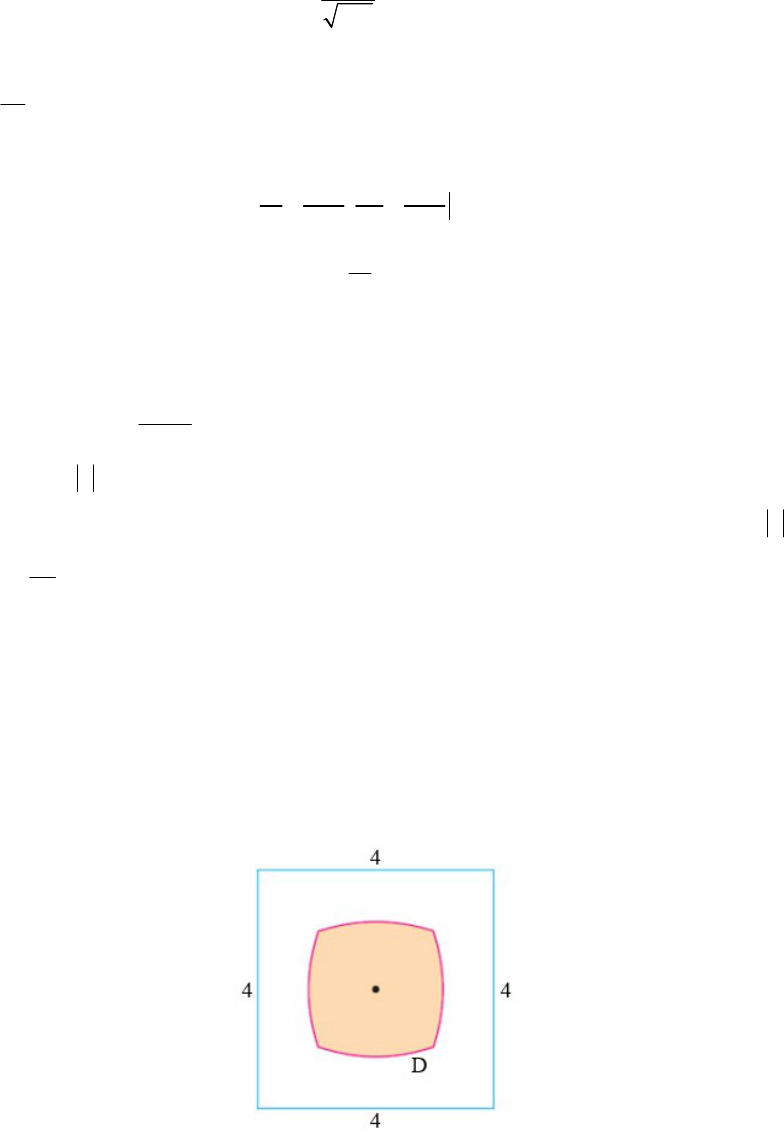
Câu 1. Hình vẽ dưới đây cho biết một miền D (được tô đậm) nằm trong hình vuông cạnh bằng 4. Miền D

này gồm những điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới cạnh gần nhất

của hình vuông. Tính diện tích miền D (kết quả làm tròn đến hàng phần chục).

Câu 2. Một thầy giáo có 16 cuốn sách khác nhau gồm 4 cuốn sách Toán, 5 cuốn sách Lí và 7 cuốn sách Hóa.

Thầy lấy ra ngẫu nhiên 8 cuốn sách để tặng cho học sinh. Tính xác suất để số sách còn lại của thầy có đủ cả

3 môn (làm tròn kết quả đến hàng phần trăm).

Câu 3. Năm 2025, một cửa hàng cần nhập về tổng cộng 600 chiếc điện thoại. Cửa hàng sẽ nhận theo nhiều

lô hàng, mỗi lô hàng chứa số lượng điện thoại bằng nhau. Chi phí vận chuyển là 50 USD cho mỗi lô hàng,

Đề thi thử tốt nghiệp môn Toán Sở Bắc Giang

Đề thi thử tốt nghiệp THPT 2025 môn Toán lần 1 Sở GD&ĐT Bắc Giang được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Bài viết được tổng hợp gồm có 2 mã đề thi. Đề thi được biên soạn theo cấu trúc đề thi mới. Mỗi đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Mời các bạn cùng theo dõi đề thi dưới đây để có thêm tài liệu ôn Thi THPT Quốc gia sắp tới nhé.

Tải về

Chọn file muốn tải về: