Đề thi thử tốt nghiệp THPT 2025 môn Toán liên trường THPT Tiền Giang
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Mã đề 0101 Trang 1/4
SỞ GD VÀ ĐT TIỀN GIANG
Đề liên trường
ĐỀ CHÍNH THỨC
(Đề thi có 04 trang)
MÃ ĐỀ 0101
KỲ THI THỬ TỐT NGHIỆP
TRUNG HỌC PHỔ THÔNG NĂM 2025
Môn thi: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian giao đề)
Ngày thi: 09/6/2025
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh làm một phương án.
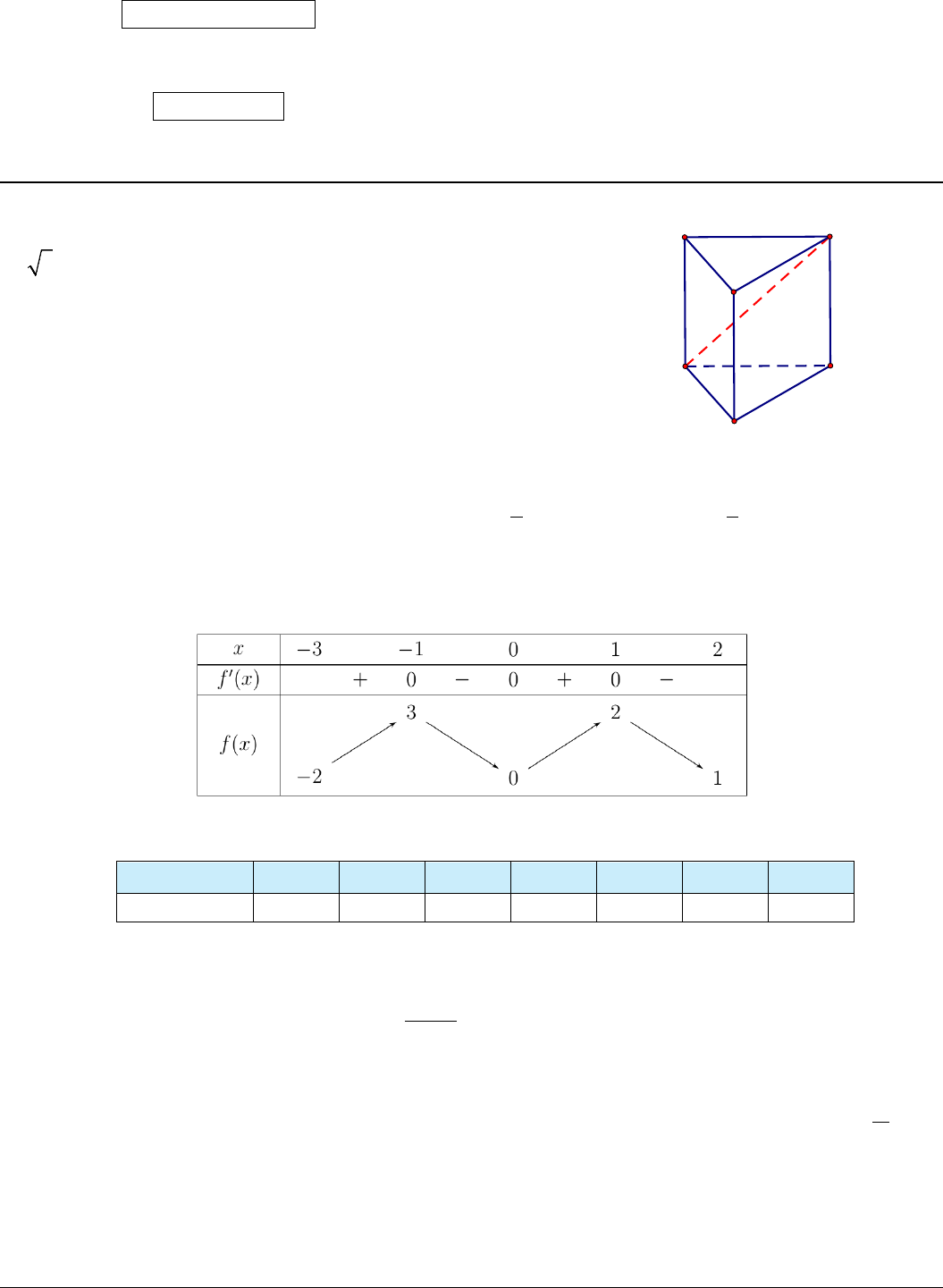
Câu 1. Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
3a
, cạnh bên
AA a
′
=
. Góc giữa đường thẳng
BC
′
và
( )
ABC
bằng bao
nhiêu?
A.
o
150
. B.
o
30
. C.
o
60
. D.
o
45
.
Câu 2. Tập nghiệm của bất phương trình
21
3 27
x
−
>
là
A.
( )
3; +∞
. B.
( )
2; +∞
. C.
1
;
2
+∞
. D.
1
;
3
+∞
.
Câu 3. Cho hàm số
( )
y fx=
liên tục trên
[ ]
3; 2−
và có bảng biến thiên như hình vẽ bên dưới. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
( )
y fx=
trên đoạn
[ ]
1; 2−
. Giá trị của
Mm+
bằng
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 4. Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Điểm
[3; 4)
[4; 5)
[5; 6)
[6; 7)
[7; 8)
[8; 9)
[9; 10)
Số học sinh
3
8
7
12
7
1
1
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A.
2, 09
. B.
6,94
. C.
4,84
. D.
2,10
.
Câu 5. Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
+
=
−
là
A.
1y =
. B.
1x =
. C.
2y =
. D.
2x =
.
Câu 6. Cho hàm số
( )
sin cosfx x x= +
và
( )
Fx
là một nguyên hàm của hàm số
( )
fx
thỏa mãn
2.
2
F
π
=
Khi đó
( )
Fx
là hàm số nào dưới đây?
A.
( )
cos sin 3Fx x x= −+
. B.
( )
cos sin 3Fx x x=−++
.
C.
( )
cos sin 1Fx x x=−+−
. D.
( )
cos sin 1Fx x x=−++
.
A'
C'
B'
C
A
B
Mã đề 0101 Trang 2/4
Câu 7. Một vật chuyển động theo phương trình
(
)
32
1
3 14 1
3
st t t t
= −++
, trong đó
0,tt>
tính bằng giây,
( )
st
tính bằng mét. Tính vận tốc tức thời của vật tại thời điểm
3t =
giây.
A.
3 m/s
. B.
5 m/s
. C.
2 m/s
. D.
6 m/s
.
Câu 8. Cho cấp số nhân
(
)
n
u
với
1
2u =
và công bội
3q
=
. Số hạng thứ 4 của cấp số nhân là
A. 24. B.
48
. C.
162
. D.
54
.
Câu 9. Trong không gian
Oxyz
, cho hai điểm
( )
2; 1; 0A −
và
( )
2; 1; 2B −
. Phương trình của mặt cầu có đường
kính
AB
là
A.
( )
2
22
1 24xy z++− =
. B.
( )
2
22
1 24xy z++− =
.
C.
( )
2
22
16xy z++− =
. D.
( )
2
22
16xy z++− =
.
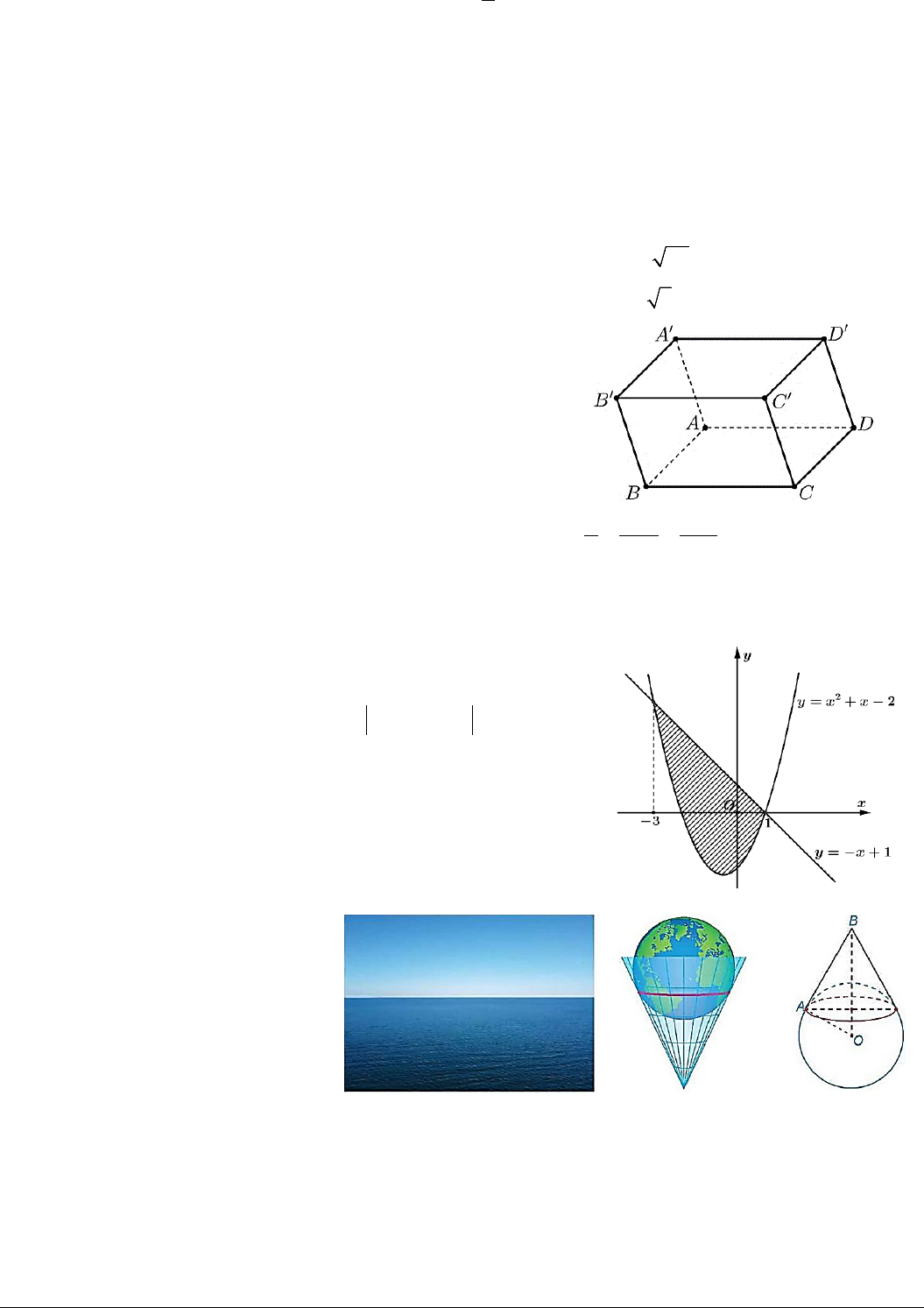
Câu 10. Cho hình hộp
.ABCD A B C D
′′′′
(minh họa như hình dưới
đây). Đặt
v BA BC BB
′′′′′
=++
. Khẳng định nào sau đây là đúng?
A.
v BD
′
=
. B.
v BD
′′
=
.
C.
v BD
′
=
. D.
v DB
′
=
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
11
:
22 5
xy z
d
+−
= =
. Một vectơ chỉ phương
của đường thẳng
d
là
A.
(
)
2
2; 2; 5u =
. B.
( )
1
0; 1;1u = −
. C.
( )
3
0; 1; 1u = −
. D.
(
)
4
2; 5; 2
u
=
.
Câu 12. Diện tích phần gạch sọc trong hình vẽ được tính theo công
thức nào dưới đây?
A.
( )
1
2
3
2 3dxx x
−
−−
∫
. B.
1
2
3
2 3dxx x
−
−− −
∫
.
C.
( )
1
2
3
2 3dxx x
−
+−
∫
. D.
( )
1
2
3
2 3dxx x
−
−− +
∫
.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Nếu đứng trước biển và nhìn
ra xa, người ta sẽ thấy một đường
giao giữa mặt biển và bầu trời, đó là
đường chân trời đối với người quan
sát (tham khảo hình vẽ 1.1). Về mặt
Vật lí, đường chân trời là đường giới
hạn phần Trái Đất mà người quan sát
có thể nhìn thấy được (phần còn lại bị
chính Trái Đất che khuất).
Hình 1.1 Hình 1.2 Hình 1.3
Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh của một chiếc nón và Trái Đất được “thả” vào trong
chiếc nón đó thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (tham khảo
hình 1.2). Trong không gian Oxyz, giả sử bề mặt Trái Đất (S) có phương trình
2 22
1++=xyz
và người quan
sát ở vị trí
( )
1; 1; 1−B
; A là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí B sao cho
0
90BAO =
(tham khảo hình 1.3)

Mã đề 0101 Trang 3/4
a) Khoảng cách từ vị trí điểm
B
đến tâm Trái Đất bằng
3
.
b) Khoảng cách giữa hai điểm
A
và
B
là
2
.
c) Điểm
A
luôn thuộc một mặt phẳng cố định.
d) Phương trình mặt cầu đường kính OB là
2 22
1 1 13
2 2 24
xyz
−+−+−=
.
Câu 2. Một tổ chức nghiên cứu đang khảo sát mối liên hệ giữa việc tài xế sử dụng điện thoại di động khi đang
lái xe và khả năng gây tai nạn giao thông. Kết quả cho thấy:
- Nếu một người tài xế sử dụng điện thoại khi đang lái xe, xác suất để người tài xế đó gây tai nạn là giao
thông là
0, 4
.
- Nếu một người tài xế không sử dụng điện thoại khi đang lái xe, xác suất người tài xế đó không gây tai nạn
giao thông là
0,95
.
- Xác suất để người tài xế đó sử dụng điện thoại khi đang lái xe là
0, 02
.
a) Nếu có
1000
người tham gia khảo sát thì có
20
người sử dụng điện thoại khi đang lái xe.
b) Nếu biết rằng người tài xế đó không sử dụng điện thoại khi đang lái xe, xác suất để người đó gây tai nạn
giao thông là
0, 05
.
c) Nếu biết rằng người tài xế đó gây tai nạn giao thông, xác suất người đó sử dụng điện thoại khi đang lái xe
là
8
57
.
d) Việc sử dụng điện thoại di động khi đang lái xe làm tăng xác suất gây tai nạn giao thông lên
10
lần so với
không sử dụng điện thoại di động khi đang lái xe.
Câu 3. Cho hàm số
( )
cos x
fx e=
.
a)
0.
2
f
π
=
b) Phương trình
( )
0fx
′
=
có 2 nghiệm trên đoạn
3
0;
2
π
.
c) Đạo hàm của hàm số đã cho là
( )
cos
sin .
x
f x xe
′
=
d) Giá trị nhỏ nhất của
( )
fx
trên đoạn
3
;
22
ππ
là
1
.
e
Câu 4. Tại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số
( )
32
20 300 1000
Bt t t t
′
=−+
, trong đó
t
tính bằng giờ
( )
0 15t≤≤
,
( )
Bt
′
tính bằng khách/giờ. Sau hai giờ,
1375
người đã có mặt tại lễ hội. Gọi
( )
Bt
(tính bằng khách) là số lượng khách tới tham dự lễ hội sau
t
giờ
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).
a) Sau một giờ có
500
khách đến tham dự lễ hội.
b)
( )
43 2
5 100 500 95.Bt t t t=−++
c) Khi
[ ]
3; 8t ∈
thì tốc độ thay đổi lượng khách tham dự lễ hội sẽ giảm.
d) Số lượng khách tới tham dự lễ hội lớn nhất là
28200
khách.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Một siêu thị có hai quầy thanh toán. Quầy 1 phục vụ 60% lượng khách hàng với tỷ lệ khách hàng có
thẻ thành viên là 30%. Quầy 2 phục vụ 40% lượng khách hàng với tỷ lệ khách hàng có thẻ thành viên là 50%.
Chọn ngẫu nhiên một người rời khỏi quầy thanh toán. Biết rằng khách hàng này có thẻ thành viên, tính xác
suất khách hàng đã thanh toán ở quầy 1. (làm tròn kết quả đến hàng phần trăm)
Đề thi thử tốt nghiệp môn Toán liên trường THPT Tiền Giang
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán liên trường THPT Tiền Giang có đáp án là tài liệu hữu ích giúp bạn đọc có thể trau dồi nội dung kiến thức, chuẩn bị thật tốt cho kì Thi THPT Quốc gia sắp tới nhé. Đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi đề thi dưới đây.


