Đề thi thử tốt nghiệp THPT 2025 môn Toán trường THPT Thị xã Quảng Trị
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Trang 1/5 - Mã đề 1111
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
KỲ THI THỬ TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2025
Bài thi: TOÁN
Thời gian làm bài : 90 phút, không kể thời gian giao đề
Chữ ký giám thị…………………………………………………………….
Họ tên thí sinh : ..................................................... Số báo danh : ...............
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
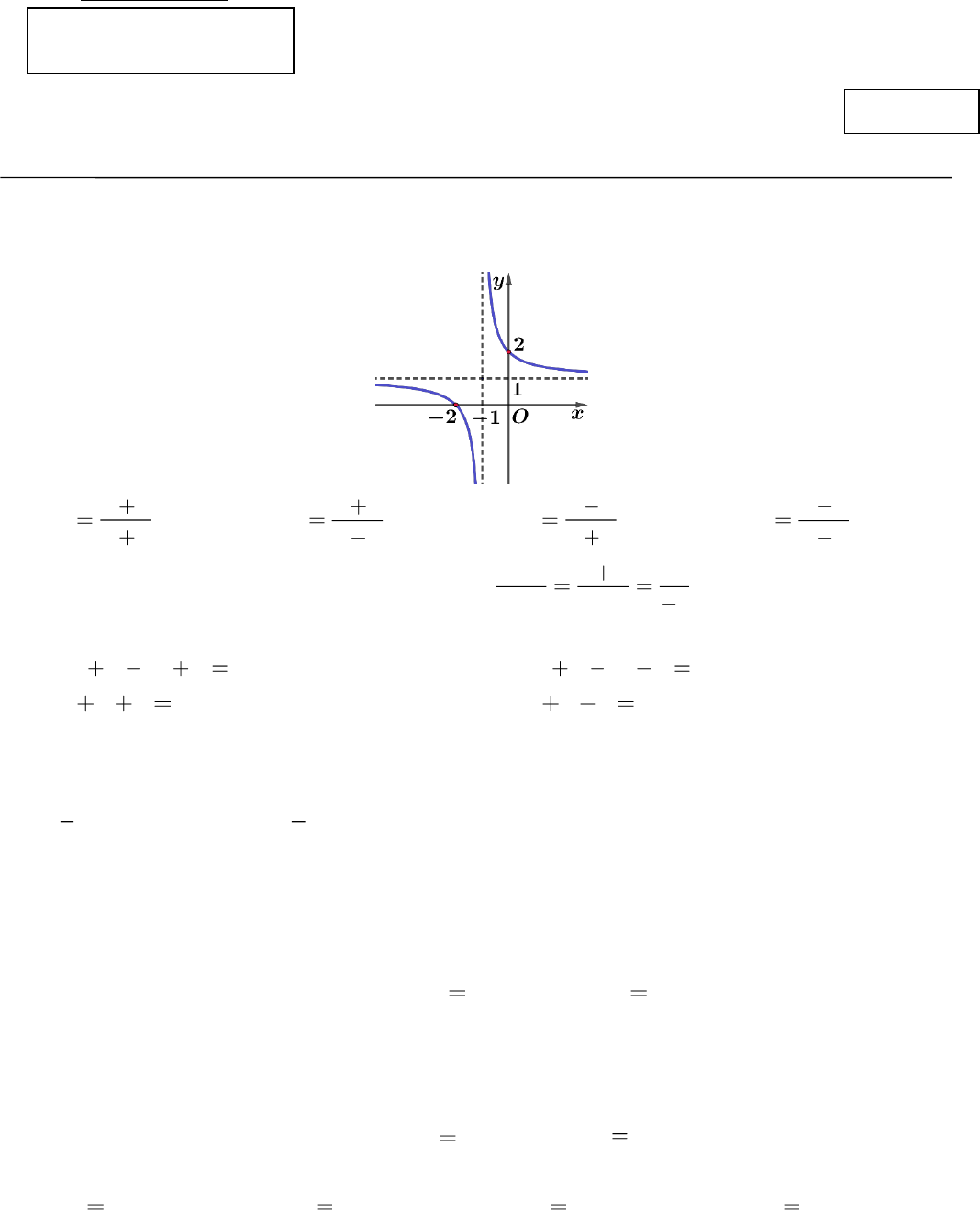
Câu 1. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A.
x
y
x
2
1
. B.
x
y
x
2
1
. C.
x
y
x
2
1
. D.
x
y
x
2
1
.
Câu 2. Trong không gian
,Oxyz
cho đường thẳng
:.
x y z
d
11
2 1 3
Mặt phẳng
()P
đi qua điểm
( ; ; )A 1 0 1
và vuông góc với đường thẳng
d
có phương trình là
A.
x y z2 3 1 0
. B.
x y z2 3 1 0
.
C.
xz10
. D.
xz10
.
Câu 3. Nếu
2
1
5f x dx
thì
2
1
4 f x dx
bằng:
A.
5
2
. B.
5
4
. C.
10
. D.
20
.
Câu 4. Cho hàm số
( ) 2
x
f x e
. Khẳng định nào dưới đây là đúng?
A.
2
()
x
f x dx e C
. B.
( ) 2
x
f x dx e x C
.
C.
( ) 2
x
f x dx e x C
. D.
()
x
f x dx e C
.
Câu 5. Thể tích của khối chóp có diện tích đáy
B 6
và chiều cao
h 3
bằng:
A.
18
. B.
6
. C.
9
. D.
3
.
Câu 6. Cho hình chóp
.S ABC
có
,SA ABC
tam giác
ABC
vuông tại
B
, kết luận nào sau đây sai?
A.
SAB SBC
B.
SAC ABC
. C.
SAC SBC
. D.
SAB ABC
.
Câu 7. Cho cấp số nhân
()
n
u
có số hạng đầu
u
1
7
và công bội
q 3
. Khi đó số hạng thứ hai của cấp số
nhân đã cho là
A.
u
2
343
. B.
u
2
21
. C.
u
2
10
. D.
u
2
49
.
Mã đề
1111
ĐỀ THI CHÍNH THỨC
(Đề có 4 trang)
(Đề có 5 trang)

Trang 2/5 - Mã đề 1111
Câu 8. Cho hàm số
()y f x
có đồ thị là đường cong trong hình vẽ. Giá trị nhỏ nhất của hàm số đã cho trên
đoạn
[ ; ]22
bằng:
A.
()f 0
. B.
()f 1
. C.
()f 1
. D.
()f 2
.
Câu 9. Đường tiệm cận xiên của đồ thị hàm số
()
xx
fx
x
2
2 3 1
1
có phương trình là
A.
yx23
. B.
yx25
. C.
yx23
. D.
yx25
.
Câu 10. Cho hàm số
()y f x
có đạo hàm
( ) ( )( ), .f x x x x21
Mệnh đề nào dưới đây đúng?
A. Hàm số đã cho đồng biến trên
( ; )1
. B. Hàm số đã cho đồng biến trên
( ; )12
.
C. Hàm số đã cho đồng biến trên
( ; )2
. D. Hàm số đã cho nghịch biến trên
( ; )12
.
Câu 11. Tập nghiệm của bất phương trình
2
3
log 2 3x
là
A.
S
. B.
5;5P
. C.
S
. D.
; 5 5;S
.
Câu 12. Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở
bảng sau:
Thời gian
(đơn vị: giây)
[ ; )0 60
[ ; )60 120
[ ; )120 180
[ ; )180 240
[ ; )240 300
[ ; )300 360
Số cuộc gọi
9
9
5
7
2
1
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên bằng:
A.
140
. B.
60
. C.
169
. D.
180
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a) , b) , c) , d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
2
.
x
y f x x e
a) Đạo hàm của hàm số đã cho là
( ) ( )e .
x
f x x x
2
2
b) Nghiệm của phương trình
()fx 0
là
x 0
và
.x 2
c) Hàm số đồng biến trên khoảng
( ; ).0
d) Giá trị nhỏ nhất của hàm số trên đoạn
[ ; ]11
bằng
.
e
1
Câu 2. Một người điều khiển xe máy với vận tốc 36 km/h thì phát hiện ở phía trước cách vị trí xe một
đoạn 50 m có công trường đang thi công có gắn biển báo giới hạn tốc độ tối đa cho phép là 20 km/h. Hai
giây sau đó, xe máy bắt đầu giảm tốc với vận tốc
1
v t at b
(
/ms
)
, , 0a b a
, trong đó
t
là thời
gian tính bằng giây kể từ khi xe bắt đầu giảm tốc độ. Khi xe máy vừa đến vị trí đặt biển báo thì tốc độ của xe
máy bằng 18 km/h và giữ nguyên vận tốc như vậy cho đến khi rời khỏi khu vực công trường. Khi vừa ra
khỏi công trường, xe máy tăng tốc với vận tốc
2 1 1
/v t mt n m s
, , 0m n m
trong đó
1
t
là thời
gian tính bằng giây kể từ khi xe máy vừa ra khỏi công trường. Biết rằng đúng 4 giây sau khi tăng tốc, xe
máy đạt vận tốc 54 km/h.
a) Quãng đường xe máy đi được từ khi phát hiện biển báo giới hạn tốc độ đến khi bắt đầu giảm tốc độ
là 20 m.
b)
15.b
c) Xe máy đến vị trí đặt biển báo tốc độ tối đa cho phép sau 4 giây kể từ khi giảm tốc.
d) Quãng đường xe máy đi được kể từ khi tăng tốc đến khi đạt vận tốc 54 km/h là 44 m.
Trang 3/5 - Mã đề 1111
Câu 3. Hải đăng là một ngọn tháp (nhà hoặc khung) được thiết kế để chiếu sáng từ một hệ thống đèn và thấu
kính, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Vào năm 293 trước Công
nguyên, ngọn hải đăng đầu tiên đã được người Phoenicia xây dựng trên hòn đảo Pharos tại Alexandria.
Trong không gian với hệ tọa độ
Oxyz
(đơn vị trên mỗi trục là mét), coi một phần mặt biển được khảo sát là
mặt phẳng
Oxy
trục
Oz
hướng lên vuông góc với mặt biển, một ngọn hải đăng có đỉnh ở vị
trí
21;35;50I
và có bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu mô tả ranh giới vùng phủ sáng trên biển của ngọn hải đăng trên
là
2 2 2
2
21 35 50 4000 .xyz
b) Người đi biển ở vị trí
5121;658;0D
thì có thể nhìn thấy được ánh sáng của ngọn hải đăng.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 m (làm tròn kết
quả đến hàng phần chục, giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển từ vị trí
5121;658;0D
di chuyển theo đường thẳng đến chân ngọn hải đăng với
tốc độ 7 hải lý/giờ (biết một hải lý bằng 1852 mét) thì mất 5,27 phút (kết quả làm tròn đến hàng phần trăm)
để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
Câu 4. Một công ty truyền thông đấu thầu hai dự án. Khả năng thắng thầu của dự án 1 và dự án 2 lần lượt
là 50% và 60%. Khả năng thắng thầu cả hai dự án của công ty là 40%. Gọi A là biến cố công ty thắng thầu
dự án 1 và B là biến cố công ty thắng thầy dự án 2.
a)
0,5PA
và
0,4.P AB
b)
| 0,8P B A
và
2
|.
3
P A B
c) Biết công ty không thắng thầu dự án 1. Khả năng công ty sẽ thắng thầu dự án 2 là 35%.
d) Xác suất công ty chỉ thắng thầu đúng một dự án là 30%.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hộp I đựng 9 quả cầu được đánh số từ 1 đến 9, hộp II đựng 6 quả cầu được đánh số từ 4 đến 9,
các quả cầu có cùng kích thước và khối lượng. Bạn An bốc ngẫu nhiên bốn quả cầu từ hộp I và lấy bốn số từ
bốn quả cầu bốc được xếp thành một số tự nhiên có các chữ số tăng dần, bạn Bình bốc ngẫu nhiên bốn quả
cầu từ hộp II và lấy bốn số từ bốn quả cầu bốc được xếp thành một số tự nhiên có các chữ số tăng dần. Tính
xác suất để An bốc được ít nhất một trong ba quả cầu có ghi số 1 hoặc ghi số 2 hoặc ghi số 3, nếu biết An có
số tự nhiên nhỏ hơn số tự nhiên của Bình. (làm tròn kết quả đến hàng phần trăm).
Câu 2. Ông An có một cái hồ có dạng tam giác đều
ABC
cạnh bằng
40 3 m
. Ông muốn chia cái hồ đó
thành hai phần: phần 1 dùng để nuôi vịt ký hiệu là hình phẳng
H
, phần 2 dùng để nuôi cá. Biết hình
phẳng
H
là tập hợp tất cả các điểm
M
nằm trong tam giác đều
ABC
và thỏa mãn
; 10 .d M AC MB
Hãy tính diện tích phần dùng để nuôi cá theo đơn vị mét vuông. ( Làm tròn kết quả đến hàng đơn vị)
Đề thi thử tốt nghiệp môn Toán trường THPT Thị xã Quảng Trị
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán trường THPT Thị xã Quảng Trị có đáp án được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Đề thi được biên soạn theo cấu trúc đề thi mới. Đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi đề thi dưới đây để có thêm tài liệu ôn thi kì Thi THPT Quốc gia sắp tới nhé.



