Đề thi thử tốt nghiệp THPT 2025 môn Toán Sở GD&ĐT Hưng Yên
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI THỬ TỐT NGHIỆP THPT NĂM 2025
HƯNG YÊN MÔN: TOÁN
ĐỀ CHÍNH THỨC Thời gian làm bài: 90 phút, không kể thời gian phát đề
Đề thi gồm có 05 trang
Họ, tên thí sinh: .................................................................... Số báo danh: ................ Mã đề 0121
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
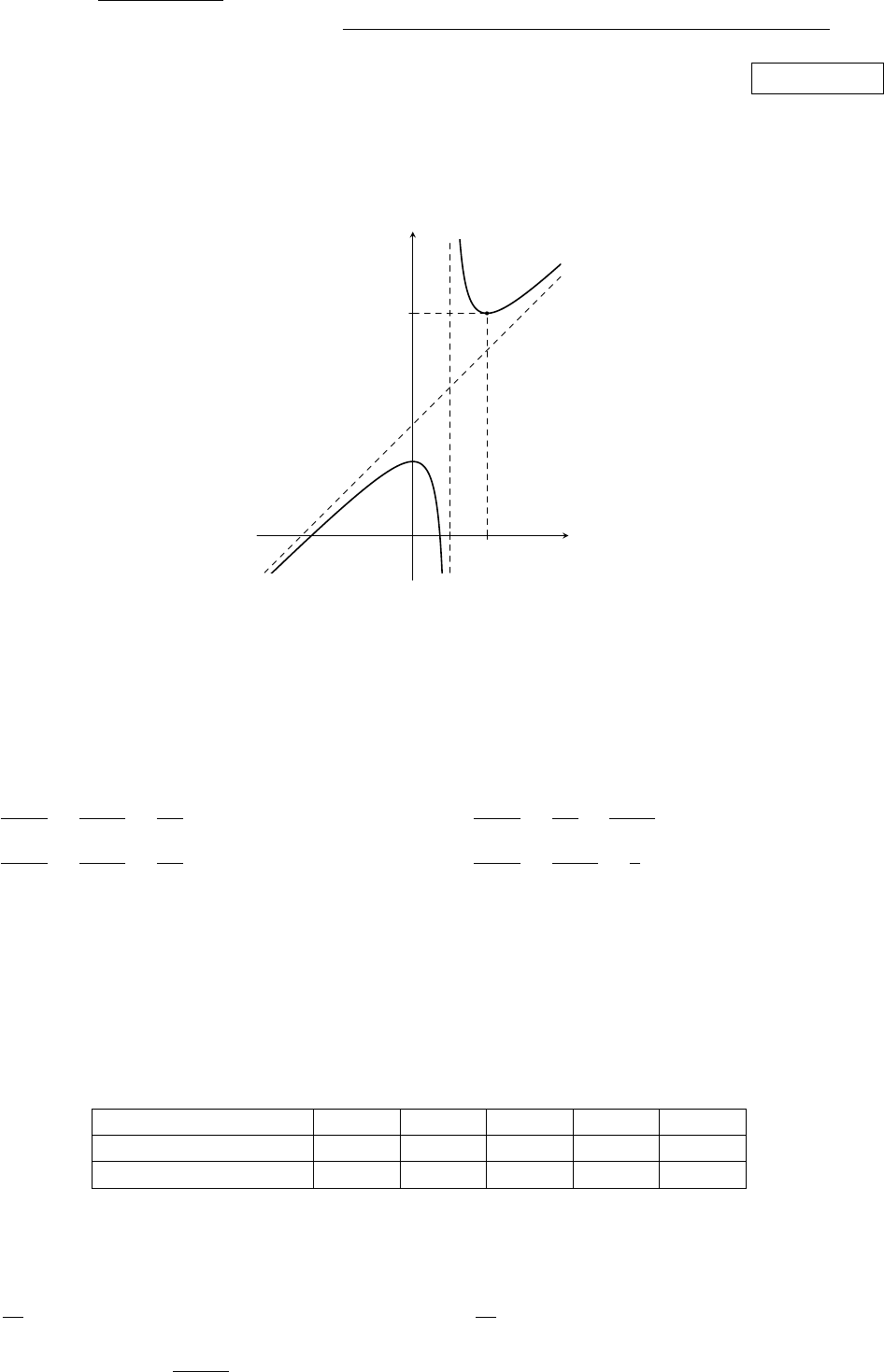
Câu 1. Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây:
x
y
O
1 2
6
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau?
A. (−∞; 1). B. (2; +∞). C. (0; 1). D. (1; 2).
Câu 2. Trong không gian Oxyz, cho mặt phẳng (P ) : 2x + y − z − 1 = 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của (P )?
A.
−→
n
3
= (2; 1; −1). B.
−→
n
1
= (2; −1; 1). C.
−→
n
4
= (−2; 1; 1). D.
−→
n
2
= (2; 1; 1).
Câu 3. Đường thẳng đi qua điểm A(1; −2; 0) và vuông góc với mặt phẳng x − 2y − 2z − 3 = 0 có phương
trình chính tắc là
A.
x + 1
1
=
y − 2
−2
=
z
−2
. B.
x − 1
1
=
y
−2
=
z + 2
−2
.
C.
x − 1
1
=
y + 2
−2
=
z
−2
. D.
x − 1
1
=
y + 2
2
=
z
2
.
Câu 4. Biết
3
Z
1
f(x) dx = 5 và
3
Z
1
g(x) dx = −7. Giá trị của
3
Z
1
[3f(x) − 2g(x)] dx bằng
A. −31. B. 29. C. 1. D. −29.
Câu 5. Nghiệm của phương trình log
2
(x − 1) = 3 là
A. x = 9. B. x = 8. C. x = 10. D. x = 7.
Câu 6. Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình:
Thời gian (phút) [10; 15) [15; 20) [20; 25) [25; 30) [30; 35)
Số ngày tập của Hưng 2 14 8 3 3
Số ngày tập của Bình 12 8 7 3 0
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục của Hưng và Bình lần lượt là
A. 20 phút và 25 phút. B. 25 phút và 20 phút. C. 20 phút và 20 phút. D. 25 phút và 25 phút.
Câu 7. Họ nguyên hàm của hàm số y = x
3
là
A.
x
4
4
+ C. B. x
4
+ C. C.
x
2
2
+ C. D. 3x
2
+ C.
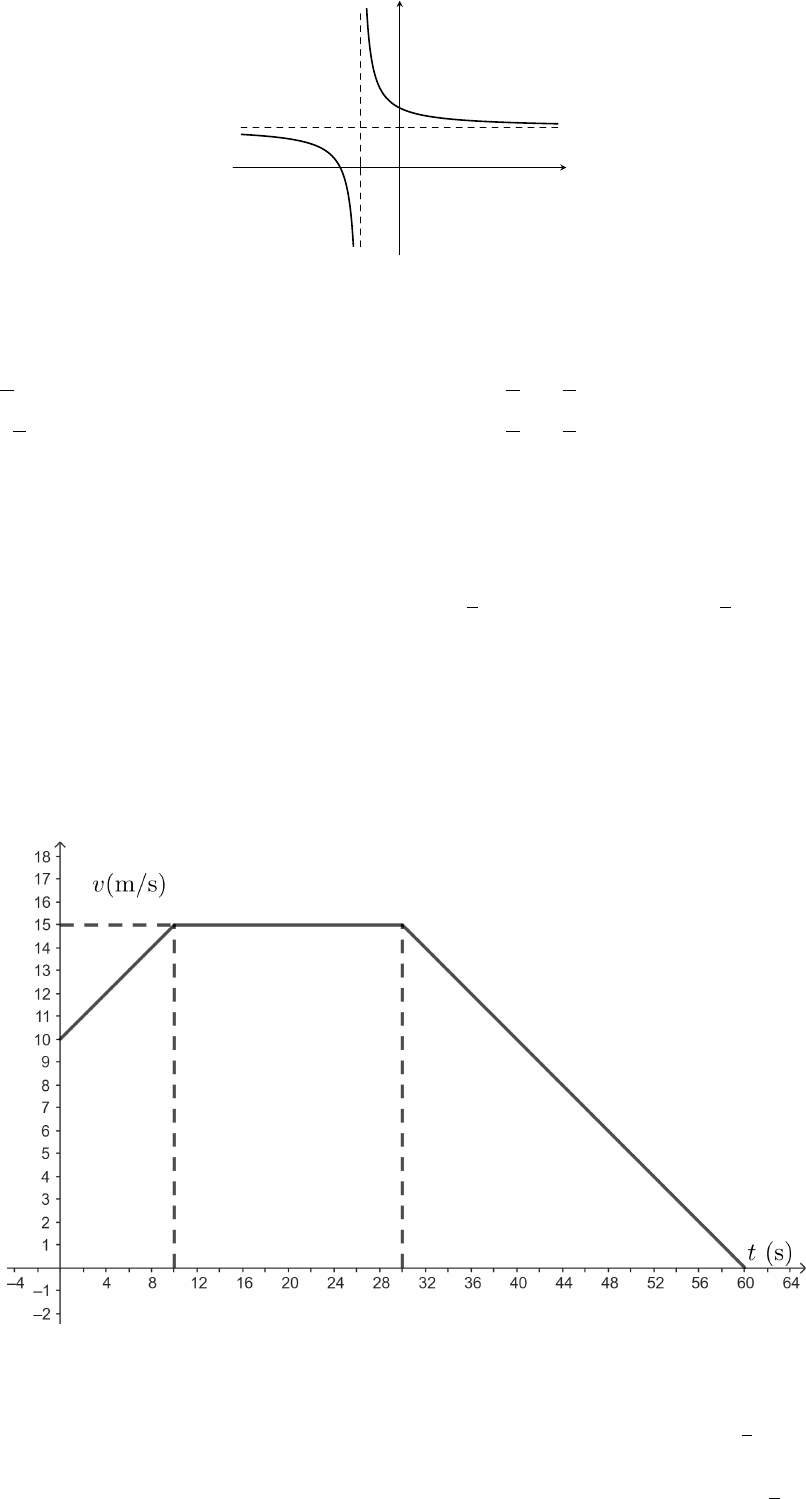
Câu 8. Cho hàm số y =
ax + b
cx + d
(c ̸= 0; ad − bc ̸= 0) có đồ thị hàm số như hình vẽ dưới đây:
1
x
y
O
−1
1
Đường tiệm cận đứng của đồ thị hàm số là
A. x = 1. B. x = −1. C. y = −1. D. y = 1.
Câu 9. Các nghiệm của phương trình cos 2x = 0 là
A. x =
π
2
+ kπ (k ∈ Z). B. x =
π
8
+ k
π
2
(k ∈ Z).
C. x = k
π
2
(k ∈ Z). D. x =
π
4
+ k
π
2
(k ∈ Z).
Câu 10. Tập nghiệm của bất phương trình 3
x
≤ 9 là
A. (−∞; 2]. B. [0; 2]. C. (0; 2). D. (−∞; 2).
Câu 11. Cho cấp số nhân (u
n
) với u
2
= 7 và công bội q = 3. Số hạng đầu tiên của cấp số nhân đã cho
bằng
A. 21. B. 4. C.
7
3
. D.
3
7
.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC, SB = SD. Trong
các khẳng định sau, khẳng định nào đúng?
A. SD ⊥ (ABCD). B. SO ⊥ (ABCD). C. SA ⊥ (ABCD). D. SC ⊥ (ABCD).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý a), b), c), d)
ở mỗi câu, thí sinh chọn đúng hoặc sai.
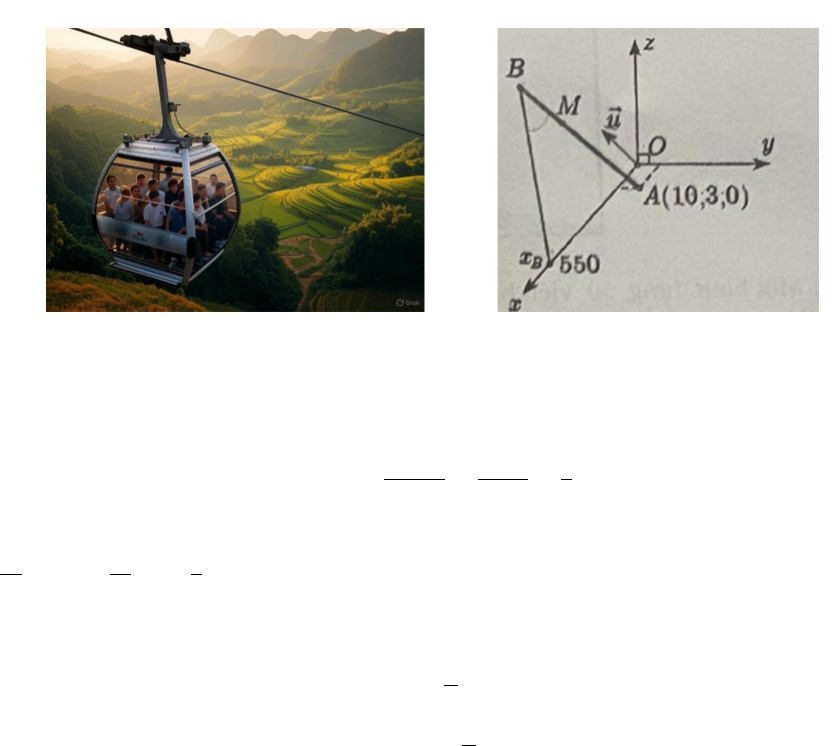
Câu 1. Một vật chuyển động thẳng có đồ thị vận tốc - thời gian như hình bên.
a) Tổng quãng đường vật đi được trong 60 (s) đầu tiên là 650 (m).
b) Trong khoảng thời gian từ 0 (s) đến 10 (s), phương trình vận tốc của vật là v(t) =
1
2
t + 10 (m/s).
c) Trong khoảng thời gian từ 30 (s) đến 60 (s), phương trình vận tốc của vật là v(t) = −
1
2
t + 30 (m/s).
2
d) Trong khoảng thời gian từ 10 (s) đến 30 (s), vật chuyển động đều.
Câu 2. Một cabin cáp treo xuất phát từ điểm A(10; 3; 0) và chuyển động đều theo đường cáp có vectơ chỉ
phương là
−→
u = (2; −2; 1) với tốc độ là 5 (m/s) (đơn vị trên mỗi trục tọa độ là mét) được mô hình hóa như
các hình vẽ sau:
a) Cabin dừng ở điểm B có hoành độ x
B
= 550. Khi đó quãng đường AB có độ dài bằng 810 (m).
b) Đường cáp AB tạo với mặt phẳng (Oxy) một góc 22
◦
(làm tròn đến hàng đơn vị của độ).
c) Phương trình chính tắc của đường cáp là
x − 10
2
=
y − 3
−2
=
z
1
.
d) Giả sử sau t giây kể từ lúc xuất phát (t ≥ 0), cabin đến vị trí điểm M. Khi đó tọa độ của điểm M là
10
3
t + 10; −
10
3
t + 3;
5
3
t
.
Câu 3. Cho hàm số f(x) = sin x − e
x
.
a) Giá trị nhỏ nhất của hàm số f(x) trên đoạn
h
0;
π
2
i
là −1.
b) Nghiệm của phương trình f
′
(x) = 0 trên đoạn
h
0;
π
2
i
là x = 0.
c) Đạo hàm của hàm số đã cho là f
′
(x) = cos x − e
x
, ∀x ∈ R.
d) f(π) = 1 − e
π
; f(0) = −2.
Câu 4. Một công ty đấu thầu hai dự án. Khả năng thắng thầu của dự án I là 0, 5 và khả năng thắng thầu
của dự án II là 0, 6. Khả năng thắng thầu cả hai dự án là 0, 4.
Gọi A là biến cố: “Thắng thầu dự án I”. Gọi B là biến cố: “Thắng thầu dự án II”.
a) Xác suất để công ty thắng thầu dự án II biết công ty không thắng thầu dự án I là 0, 2.
b) Xác suất để công ty thắng thầu đúng một dự án bằng 0, 5.
c) Xác suất để công ty thắng thầu dự án II biết công ty thắng thầu dự án I là 0, 8.
d) A và B là hai biến cố độc lập.
PHẦN III. Câu trắc nghiệm trả lời ngắn Thí sinh trả lời từ câu 1 đến câu 6 .
Câu 1. Câu lạc bộ thiện nguyện của một trường THPT dự định làm các bình hoa bằng giấy để bán trong
một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm một bình hoa nhỏ và sẽ bán với giá 100 nghìn đồng và 90
phút để làm một bình hoa lớn và bán với giá 200 nghìn đồng. Câu lạc bộ này chỉ thu xếp được 15 giờ nghỉ
để làm và ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa. Số tiền lớn nhất mà câu lạc bộ có thể thu về
là bao nhiêu? (Đơn vị: nghìn đồng)
3
Đề thi thử tốt nghiệp môn Toán Sở Hưng Yên
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán Sở GD&ĐT Hưng Yên được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo để có thêm tài liệu ôn thi kì Thi THPT Quốc gia sắp tới nhé. Đề thi được biên soạn theo cấu trúc đề thi mới. Mỗi đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Mời các bạn cùng theo dõi đề thi dưới đây.


