Đề thi thử THPT Quốc gia môn Toán - Đề 6
Luyện đề thi THPT Quốc gia môn Toán
Để chuẩn bị hiệu quả cho kỳ Thi tốt nghiệp THPT Quốc gia năm 2025 - 2026, việc luyện tập với các đề thi thử môn Toán có đáp án là bước quan trọng giúp học sinh đánh giá năng lực, rèn kỹ năng xử lý câu hỏi trắc nghiệm và nâng cao tốc độ làm bài. Bài viết này giới thiệu Đề thi thử THPT Quốc gia môn Toán – Đề 6, được biên soạn bám sát cấu trúc đề minh họa, đi kèm đáp án để bạn dễ dàng tự kiểm tra và củng cố kiến thức. Đây là tài liệu cần thiết giúp bạn tăng tốc hiệu quả trong giai đoạn ôn luyện.
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2025 – 2026
ĐỀ ÔN TẬP SỐ 6
THỜI GIAN: 90 PHÚT. NGÀY … /…/2026
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
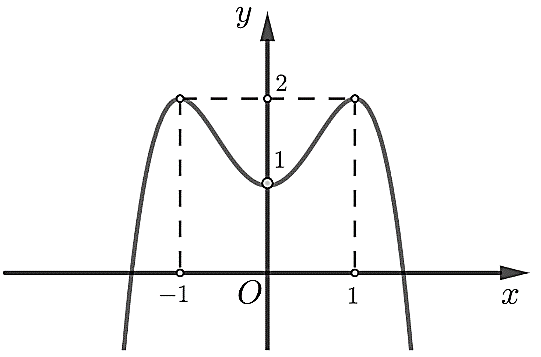
Câu 1: Cho hàm số 
\(y = f(x)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. \((0;1)\). B. \(( - \infty;0)\). C. \((1; + \infty)\). D. \(( - 1;0)\).
Câu 2: Thống kê điểm kiểm tra giữa kỳ 1 môn Toán của 30 học sinh lớp 12C1 của một trường THPT được ghi lại ở bảng sau:
|
Điểm |
\(\lbrack 2;4)\) |
\(\lbrack 4;6)\) |
\(\lbrack 6;8)\) |
\(\lbrack 8;10)\) |
|
Số học sinh |
4 | 8 | 11 | 7 |
Trung vị của mẫu số liệu gốc thuộc khoảng nào trong các khoảng dưới đây?
A. \(\lbrack 2;4)\). B. \(\lbrack 4;6)\). C. \(\lbrack 6;8)\). D. \(\lbrack 8;10)\).
Câu 3: Trong không gian \(Oxyz\), một vectơ pháp tuyến của mặt phẳng \(\frac{x}{- 2} + \frac{y}{- 1} + \frac{z}{3} =
1\) là
A. \(\overrightarrow{n} = (3\ ;\ \ 6\ ;\ -
2).\) B. \(\overrightarrow{n} = (2\
;\ - 1\ ;3).\)
C. \(\overrightarrow{n} = ( - 3; - 6\ ;\ -
2).\) D. \(\overrightarrow{n} = ( - 2;
- 1;3).\)
Câu 4: Cho cấp số cộng \((u_{n})\) với số hạng đầu \(u_{1} = - 6\) và công sai \(d = 4.\) Tính tổng \(S\) của 14 số hạng đầu tiên của cấp số cộng đó.
A. \(S = 46\). B. \(S = 308\). C. \(S = 644\). D. \(S = 280\).
Câu 5: Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Tích vô hướng \(\overrightarrow{AB} \cdot
\overrightarrow{AC}\) bằng:
A. \(a^{2}\). B. \(- a^{2}\). C. \(\frac{1}{2}a^{2}\). D. \(\frac{\sqrt{3}}{2}a^{2}\).
Câu 6: Giá trị lớn nhất của hàm số \(f(x) =
x^{3} - 8x^{2} + 16x - 9\) trên đoạn \(\lbrack 1;3\rbrack\) là:
A. \(\max_{\lbrack 1;3\rbrack}f(x) =
0.\) B. \(\max_{\lbrack 1;3\rbrack}f(x)
= \frac{13}{27}.\) C. \(\max_{\lbrack 1;3\rbrack}f(x) = -
6.\) D. \(\max_{\lbrack 1;3\rbrack}f(x)
= 5.\)
Câu 7: Trong một phép thử với \(A,\ \
B\) là hai biến cố bất kì, biết rằng \(P(A) = 0,5\); \(P(AB) = 0,3\). Khi đó \(P(B|A)\) bằng:
A. \(0,6\). B. \(0,15\). C. \(0,7\). D. \(0,35\).
Câu 8: Cho biết \(\int_{1}^{3}{f(x)dx} =
3\), giá trị của \(\int_{1}^{3}{\frac{1}{3}f(x)dx}\) bằng
A. \(2\). B. \(1\). C. \(\frac{1}{3}\). D. \(3\).
Câu 9: Tập nghiệm của bất phương trình \(2^{x} \leq 4\) là:
A. \(( - \infty;2\rbrack\). B. \(\lbrack 0;2\rbrack\). C. \(( - \infty;2)\). D. \((0;2)\).
Câu 10: Phát biểu nào sau đây là đúng?
A. \(\int^{}\frac{1}{x}dx = |x| +
C\). B. \(\int^{}\frac{1}{x}dx = \ln|x|
+ C\).
C. \(\int^{}\ln xdx = x + C\). D. \(\int^{}\ln|x|dx = \ln x + C\).
Câu 11: Bạn An rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày của bạn An được thống kê lại ở bảng sau:
Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?
A. \(31,25\). B. \(31,26\). C. \(5,4\). D. \(5,6\).
Câu 12: Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta:\ \frac{x - 2}{- 3} = \frac{y}{1} = \frac{z
+ 1}{2}\). Gọi \(M\) là giao điểm của \(\Delta\) với mặt phẳng \((P):\ x + 2y - 3z + 2 = 0\). Tọa độ điểm \(M\) là:
A. \(M(2;0; - 1)\). B. \(M(5; - 1; - 3)\). C. \(M(1;0;1)\). D. \(M( - 1;1;1)\).
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 13: Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được \(x\) vải lụa \((1 \leq x \leq 18)\).Tổng chi phí sản xuất \(x\) mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí\(C(x) = x^{3} -
3x^{2} - 20x + 500.\) Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi \(B(x)\) là số tiền bán được và \(L(x)\) là lợi nhuận thu được khi bán \(x\) mét vải lụa.
a) Lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm có thể đạt được là 1200 nghìn đồng.
b) Biểu thức tính \(L(x)\) theo \(x\) là \(L(x) = - x^{3} + 3x^{2} + 220x - 500\) (nghìn đồng).
c) Hộ làm nghề dệt này cần sản xuất và bán ra mỗi ngày 10 mét vải lụa để thu được lợi nhuận tối đa.
d) Biểu thức tính \(B(x)\) theo \(x\) là \(B(x) = 220 + x\)(nghìn đồng).
Câu 14: Trong không gian \(Oxyz\), cho hai điểm \(M(2;3; - 1),N( -
1;0;1)\).
a) Hình chiếu của điểm \(M\) trên mặt phẳng \((Oyz)\) có tọa độ là \((0;3; - 1)\).
b) Tọa độ điểm\(Q\) thuộc \((Oyz)\) sao cho \(Q;M;N\) thẳng hàng là\(Q\left( 0;1;\frac{1}{3} \right)\).
c) Cho \(P(5;m + 1;3)\). Tam giác \(MNP\) vuông tại \(N\) khi và chỉ khi \(m = 1\).
d) Gọi \((\alpha)\) là mặt phẳng trung trực của đoạn \(MN\). Khi đó \((\alpha)\) có phương trình: \(3x + 3y - 2z + 6 = 0\).
Câu 15: Hằng ngày, mặt Trời chiếu sáng, bóng của một toà chung cư cao \(40\ m\) in trên mặt đất, độ dài bóng của toà nhà này được tính bằng công thức\(S(t)
= 40\left| \cot\frac{\pi}{12}t \right|,\)ở đó \(S\) được tính bằng mét, còn \(t\) là số giờ tính từ 6 giờ sáng.
a) Vào lúc 13h00 bóng của toà nhà có độ dài bằng \(0\ m\).
b) Độ dài bóng của toà nhà tại thời điếm 8 giờ sáng là \(20\sqrt{3}\ m\).
c) Tại thời điểm 5 giờ 45 chiều tối, kết quả được làm tròn đến hàng phần trăm độ dài bóng của toà nhà là \(56,86(\
m)\).
d) Tại thời điểm 9 giờ sáng hoặc 3 giờ chiều thì bóng của toà nhà dài bằng chiều cao của toà nhà.
Câu 16: Cho hàm số \(f(x) = \frac{3x +
1}{x}\).
a) Gọi \(H(x)\) là một nguyên hàm của hàm số \(f(x)\) và thỏa mãn \(H( - 1) = 3\). Khi đó \(H( - 5) = - 9 - ln5\).
b) Gọi \(G(x)\) là một nguyên hàm của hàm số \(f(x)\). Biết \(G(2) = 1\) và \(G(5) + G( - 5) = 0\). Khi đó tìm được \(G( - 10) = aln10 + bln5 + cln2 + d\), với \(a,\ b,\ c\) là các số hữu tỷ. Khi đó \(a + b + c + d = - 25.\)
c) Gọi \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) và thỏa mãn \(F(1) = 1\). Khi đó với \(x > 0\)thì \(F(x) = 3x + \ln x - 2\).
d) \(\int_{}^{}{f(x)\ }dx =
\frac{3x^{2}}{2} + \ln|x| + C\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1: Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \((ABCD)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA,EB,EC\),\(ED\) có độ dài bằng nhau và cùng tạo với mặt phẳng \((ABCD)\) một góc \(60^{\circ}\) (Hình 4).
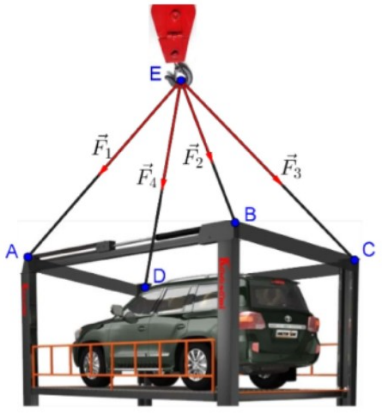
Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết rằng các lực căng \({\overrightarrow{F}}_{1},\overrightarrow{F_{2}},\overrightarrow{F_{3}},\overrightarrow{F_{4}}\) đều có cường độ là \(6000\sqrt{3}\
(N)\), trọng lượng của khung sắt là \(2500\ (N)\) và gia tốc rơi tự do là \(g = 9,8\ (m/s^{2})\). Tính khối lượng của chiếc xe ô tô theo đơn vị kilogam (kết quả làm tròn đến hàng đơn vị).
Trả lời:
Câu 2: Một đoàn tình nguyện đến một trường tiểu học miền núi để trao tặng \(20\) suất quà cho \(10\) em học sinh nghèo học giỏi. Trong \(20\) suất quà đó gồm \(7\) chiếc áo mùa đông,\(9\)thùng sữa tươi và \(4\) chiếc cặp sách. Tất cả các suất quà đều có giá trị tương đương nhau. Biết rằng mỗi em nhận \(2\) suất quà khác loại (ví dụ một chiếc áo và một thùng sữa tươi). Trong số các em nhận quà có hai em An và Bình. Tính xác suất để hai em đó nhận được suất quà giống nhau?
Trả lời:
Câu 3: Số lượng loại vi khuẩn \(A\) trong một phòng thí nghiệm được tính theo công thức \(s(t) = s(0).2^{t},\) trong đó \(s(0)\) là số lượng vi khuẩn \(A\) lúc ban đầu, \(s(t)\) là số lượng vi khuẩn \(A\) có sau \(t\) phút. Biết sau 3 phút thì số vi khuẩn \(A\) là \(625\) nghìn con. Hỏi sau bao nhiêu phút kể từ lúc ban đầu, số lượng loại vi khuẩn \(A\) là \(20\) triệu con?
Trả lời:
Câu 4: Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là \(14\ m\) và \(10\ m\) (hình bên).
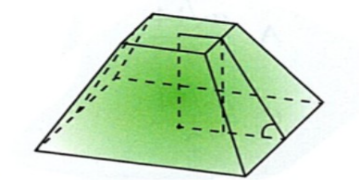
Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng \(135^{{^\circ}}\). Tính số mét khối đất cần phải di chuyển ra khỏi hầm (kết quả được làm tròn đến hàng đơn vị)
Trả lời:
Câu 5: Cổng chính trường của một THPT có 2 cánh cửa kẽm, sơn tĩnh điện, bằng nhau và có hoạ tiết giống hệt nhau. Khi khép cửa tạo ra một đường khép kín ABGCDEF.
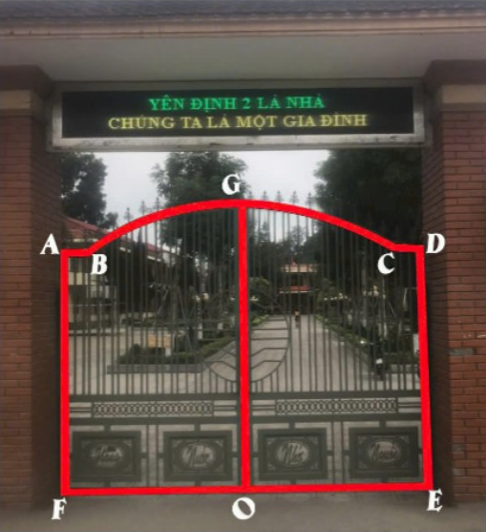
Biết \(AF = DE =
2,7(m);AB = CD = 0,5(m);EF = 4(m)\),\(OG = 3(m)\), điểm \(O\) là trung điểm của \(EF,\) đường cong \(BGC\) là cung tròn có bán kính bằng \(OG\) (\(G\) là trung điểm của cung \(BC\)). Do đã sử dụng lâu năm nên lớp sơn tĩnh điện đã bị xuống cấp, bong tróc. Nhà trường muốn sơn làm mới lại cửa, giá thành để sơn và làm mới lại cửa là 300 nghìn đồng trên một \(m^{2}\)diện tích cửa. Hỏi nhà trường phải trả khoản tiền bằng bao nhiêu triệu đồng (kết quả được làm tròn đến hàng phần trăm).
Trả lời:
Câu 6: Trong một căn phòng dạng hình hộp chữ nhật với chiều dài \(8m\), rộng \(6m\) và cao \(4m\)có \(2\) cây quạt treo tường. Cây quạt \(A\) treo chính giữa bức tường \(8m\) và cách trần \(1m\), cây quạt \(B\) treo chính giữa bức tường \(6m\) và cách trần \(1,5m\). Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ bên dưới (đơn vị: mét).
Biết điểm \(M(x;y;z)\) thuộc mặt phẳng chứa sàn nhà sao cho \(\left|
\overrightarrow{MA} - 2\overrightarrow{MB} \right|\) là nhỏ nhất, tính \(x^{2} + y^{2} + z^{2}\).
Trả lời:
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
