Đề thi thử tốt nghiệp THPT 2025 môn Toán bám sát đề minh họa - Đề 56
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
Word + PDF
Phân loại:
Tài liệu Tính phí
BÁM SÁT ĐỀ MINH HỌA
ĐỀ 56
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2025
MÔN: TOÁN
Thời gian làm bài 90 phút; không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Họ nguyên hàm của hàm số
x
f x e x
là
A.
2x
e x C
B.
2
1
2
x
e x C
C.
2
11
12
x
e x C
x
D.
1
x
eC
Câu 2: Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
. Mệnh đề nào dưới
đây đúng?
A.
2
2
0
ed
x
Sx
B.
2
0
ed
x
Sx
C.
2
0
ed
x
Sx
D.
2
0
ed
x
Sx
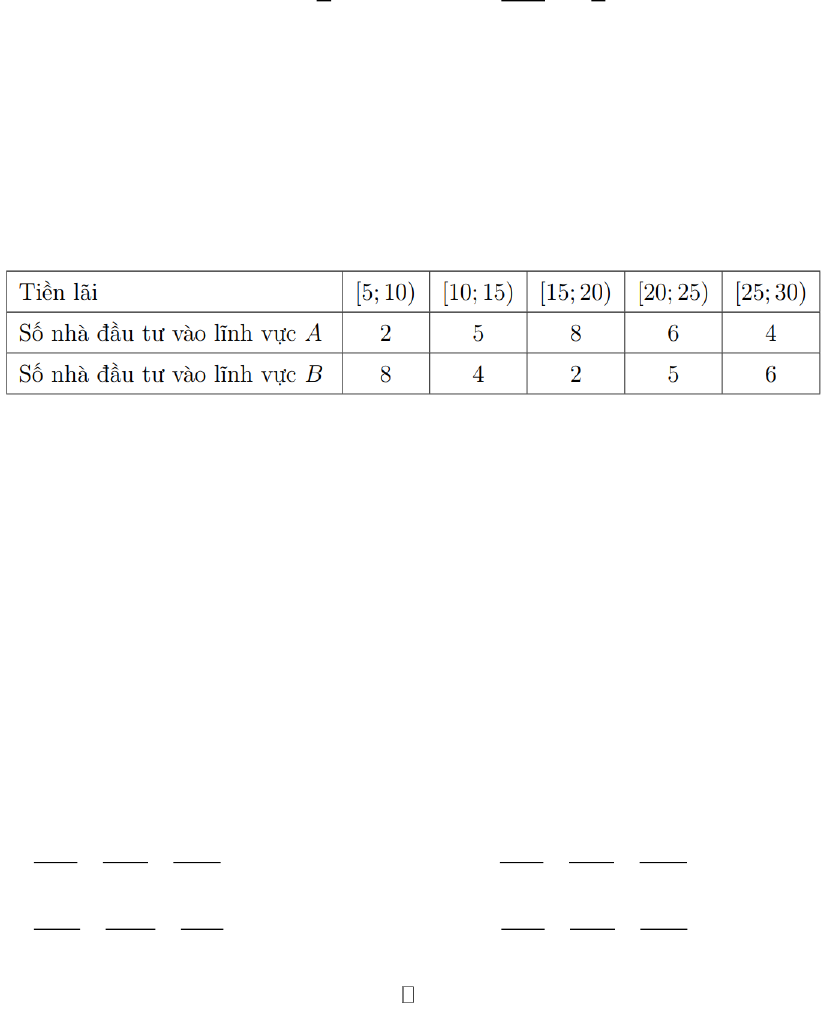
Câu 3: Người ta ghi lại tiền lãi của một số nhà đầu tư, khi đầu tư vào hai lĩnh vực
,AB
cho kết quả như sau
Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro đầu tư các lĩnh vực có giá
trị trung bình tiền lãi gần bằng nhau. Lĩnh vực nào có phương sai, độ lệch chuẩn tiền lãi cao hơn thì
được coi là có độ rủi ro lớn hơn.
Theo quan điểm trên, độ rủi ro của cổ phiếu nào cao hơn?
A. Lĩnh vực
A
có độ rủi ro bằng lĩnh vực
B
.
B. Lĩnh vực
A
có độ rủi ro cao hơn lĩnh vực
B
.
C. Lĩnh vực
A
có độ rủi ro thấp hơn lĩnh vực
B
.
D. Không so sánh được.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1;1;2A
,
2; 1;3B
. Viết phương trình đường
thẳng
AB
.
A.
1 1 2
3 2 1
x y z
B.
1 1 2
1 2 1
x y z
C.
3 2 1
1 1 2
x y z
D.
1 1 2
3 2 1
x y z
Câu 5: Cho hàm số
fx
xác định, liên tục trên
\1
và có bảng biến thiên như sau:
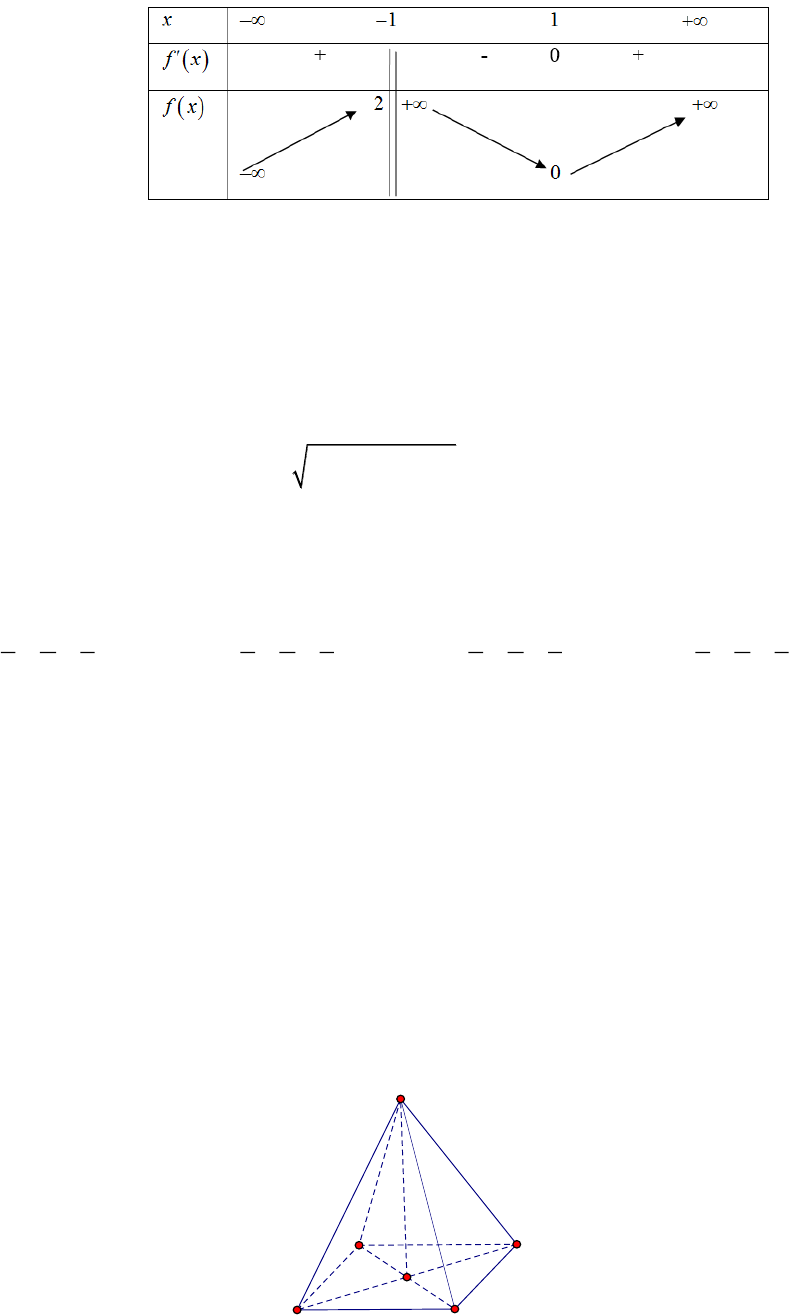
Khẳng định nào sau đây là sai?
A. Hàm số đã cho đạt cực tiểu tại
1.x
B. Đồ thị hàm số không có tiệm cận đứng.
C. Đồ thị hàm số không có tiệm cận ngang.
D. Hàm số không có đạo hàm tại
1.x
Câu 6: Tìm tập xác định của hàm số
2
log 3 1y x x
?
A.
; 5 2;
. B.
2;
. C.
1;
. D.
; 5 5;
Câu 7: Mặt phẳng đi qua ba điểm
0;0;2A
,
1;0;0B
và
0;3;0C
có phương trình là
A.
1
1 3 2
x y z
. B.
1
1 3 2
x y z
. C.
1
2 1 3
x y z
. D.
1
2 1 3
x y z
.
Câu 8: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi,
SA SC
. Khẳng định nào sau đây đúng?
A. Mặt phẳng
SBD
vuông góc với mặt phẳng
ABCD
.
B. Mặt phẳng
SBC
vuông góc với mặt phẳng
ABCD
.
C. Mặt phẳng
SAD
vuông góc với mặt phẳng
ABCD
.
D. Mặt phẳng
SAB
vuông góc với mặt phẳng
ABCD
.
Lời giải
Chọn A
O
C
A
B
D
S
Gọi
O AC BD
.
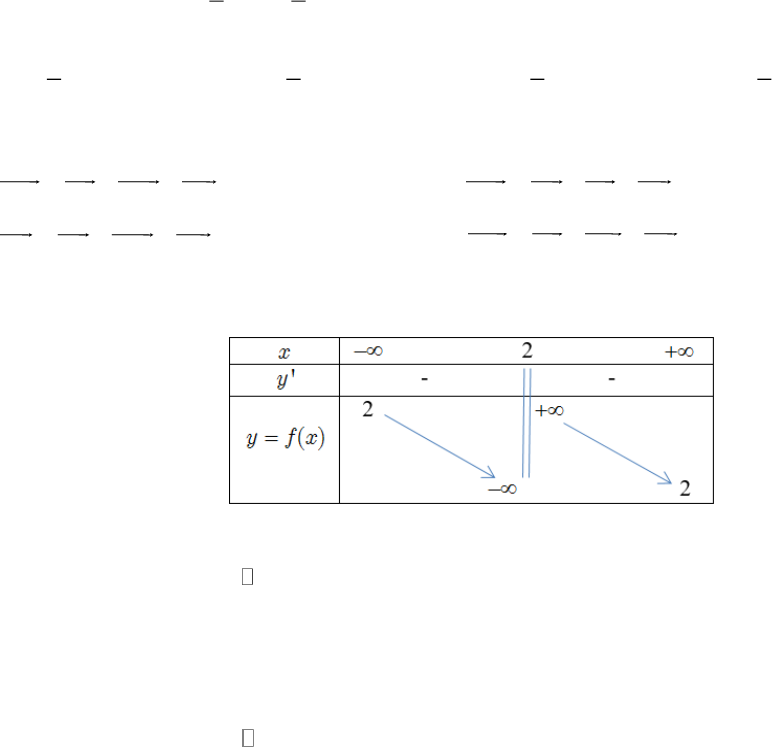
Tứ giác
ABCD
là hình thoi nên
AC BD
.
Mặt khác tam giác
SAC
cân tại
S
nên
SO AC
.
Từ và suy ra
AC SBD
nên
SBD ABCD
.
Câu 9: Số nghiệm của phương trình
2
21
xx
là
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 10: Cho dãy số
n
u
có:
1
11
;
44
ud
. Khẳng định nào sau đây đúng?
A.
5
5
4
S
. B.
5
4
5
S
. C.
5
5
4
S
. D.
5
4
5
S
.
Câu 11: Cho hình hộp
. ' ' ' 'ABCD A B C D
. Chọn đẳng thức vectơ đúng:
A.
''DB DA DD DC
. B.
'AC AC AB AD
.
C.
'DB DA DD DC
. D.
''AC AB AB AD
.
Câu 12: Hàm số
y f x
có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên
\2
.
B. Hàm số đồng biến trên
;2 2;
.
C. Hàm số nghịch biến trên
;2
và
2;
.
D. Hàm số nghịch biến trên .
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc
sai.
Câu 1: Cho hàm số
()
x
f x e x
.
a) Tính
(0) 1f
và
(ln 2) 2 ln2f
.
b) Đạo hàm của hàm số đã cho là
'
( ) 1
x
f x e
.
c) Nghiệm của phương trình
'
( ) 0fx
trên đoạn
0;1
là
2
d) Giá trị lớn nhất của
fx
trên đoạn
0;ln2
là
2 ln2
.
Đề thi thử bám sát đề minh họa 2025 môn Toán - Đề 56
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán bám sát đề minh họa - Đề 56 có đáp án là tài liệu hữu ích giúp bạn đọc có thể trau dồi nội dung kiến thức, chuẩn bị thật tốt cho kì thi tốt nghiệp THPT Quốc gia sắp tới nhé. Đề thi được biên soạn theo cấu trúc đề thi mới. Đề thi được tổng hợp gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi đúng sai và 6 câu hỏi trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi bài viết dưới đây.


