VnDoc.com

Đề thi thử THPT Quốc gia môn Toán - Đề 3

Thi THPT Quốc gia năm 2026

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Đề thi

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Luyện đề thi THPT Quốc gia môn Toán

Để chuẩn bị hiệu quả cho kỳ Thi THPT Quốc gia năm 2025 - 2026, việc luyện tập với các đề thi thử môn Toán có đáp án là bước quan trọng giúp học sinh đánh giá năng lực, rèn kỹ năng xử lý câu hỏi trắc nghiệm và nâng cao tốc độ làm bài. Bài viết này giới thiệu Đề thi thử THPT Quốc gia môn Toán – Đề 3, được biên soạn bám sát cấu trúc đề minh họa, đi kèm đáp án để bạn dễ dàng tự kiểm tra và củng cố kiến thức. Đây là tài liệu cần thiết giúp bạn tăng tốc hiệu quả trong giai đoạn ôn luyện.

ĐỀ THI THỬ THPT QUỐC GIA NĂM 2025 – 2026

ĐỀ ÔN TẬP SỐ 3

THỜI GIAN: 90 PHÚT. NGÀY … /…/2026

PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Tìm nguyên hàm của hàm số $f(x) = \frac{1}{5x - 12}$ $f(x) = \frac{1}{5x - 12}$

A. $\int_{}^{}\frac{dx}{5x - 12} = \frac{1}{5}\ln|12 - 5x| + C$ $\int_{}^{}\frac{dx}{5x - 12} = \frac{1}{5}\ln|12 - 5x| + C$. B. $\int_{}^{}\frac{dx}{5x - 12} = - \frac{1}{5}\ln|5x - 12| + C$ $\int_{}^{}\frac{dx}{5x - 12} = - \frac{1}{5}\ln|5x - 12| + C$.

C. $\int_{}^{}\frac{dx}{5x - 12} = 5ln|5x - 12| + C$ $\int_{}^{}\frac{dx}{5x - 12} = 5ln|5x - 12| + C$. D . $\int_{}^{}\frac{dx}{5x - 12} = \ln|5x - 12| + C$ $\int_{}^{}\frac{dx}{5x - 12} = \ln|5x - 12| + C$.

Câu 2: Trong không gian $Oxyz$, phương trình nào sau đây là phương trình chính tắc của đường thẳng $d:\left\{ \begin{matrix} x = - 1 + 2t \\ y = 3t \\ z = - 3 + t \end{matrix} \right.$ $d:\left\{ \begin{matrix} x = - 1 + 2t \\ y = 3t \\ z = - 3 + t \end{matrix} \right.$

A. $\frac{x + 1}{2} = \frac{y}{3} = \frac{z - 3}{- 2}$ $\frac{x + 1}{2} = \frac{y}{3} = \frac{z - 3}{- 2}$. B. $\frac{x - 1}{1} = \frac{y}{3} = \frac{z + 3}{- 2}$ $\frac{x - 1}{1} = \frac{y}{3} = \frac{z + 3}{- 2}$.

C. $\frac{x + 1}{2} = \frac{y - 3}{3} = \frac{z + 3}{1}$ $\frac{x + 1}{2} = \frac{y - 3}{3} = \frac{z + 3}{1}$. D. $\frac{x + 1}{2} = \frac{y}{3} = \frac{z + 3}{1}$ $\frac{x + 1}{2} = \frac{y}{3} = \frac{z + 3}{1}$.

Câu 3: Cho hình hộp $ABCD.EFGH$ (minh họa hình bên).

Kết quả của phép toán $\overrightarrow{AB} - \overrightarrow{EH}$ $\overrightarrow{AB} - \overrightarrow{EH}$ là

A. $\overrightarrow{FH}$ $\overrightarrow{FH}$. B. $\overrightarrow{BH}$ $\overrightarrow{BH}$. C. $\overrightarrow{DB}$ $\overrightarrow{DB}$. D . $\overrightarrow{AE}$ $\overrightarrow{AE}$ .

Câu 4: Cô Hải thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở sân trường thu được mẫu số liệu ghép nhóm sau:

Đường kính (cm)	[40; 45)	[45; 50)	[50; 55)	[55; 60)	[60; 65)
Tần số	5	20	18	7	3

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

A. $6$. B. $25$. C. $15$. D. $30$.

Câu 5: Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ bên dưới. Hàm số $y = f(x)$ đồng biến trên khoảng nào dưới đây:

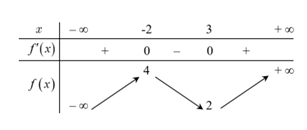
A. $( - 1;2).$ B. $( - 8; - 3).$ C. $( - \infty;4).$ $( - \infty;4).$ D. $(2; + \infty).$ $(2; + \infty).$

Câu 6: Cho hình chóp có diện tích mặt đáy là $4a^{2}$ $4a^{2}$ và chiều cao bằng $3a$. Thể tích của khối chóp tương ứng bằng:

A. $4a^{3}$ $4a^{3}$. B. $12a^{3}$ $12a^{3}$. C. $2a^{3}$ $2a^{3}$. D. $6a^{3}$ $6a^{3}$.

Câu 7: Cho hình phẳng $(H)$ giới hạn bởi các đường $y = x^{2} + 3,y = 0,x = 0,x = 5$ $y = x^{2} + 3,y = 0,x = 0,x = 5$. Gọi $V$là thể tích của khối tròn xoay được tạo thành khi quay $(H)$ xung quanh trục $Ox$. Mệnh đề nào dưới đây đúng?

A. $V = \int_{0}^{5}{(x^{2} + 3)}\ dx$ $V = \int_{0}^{5}{(x^{2} + 3)}\ dx$. B. $V = \pi\int_{0}^{5}{(x^{2} + 3)^{2}}dx$ $V = \pi\int_{0}^{5}{(x^{2} + 3)^{2}}dx$.

C. $V = \int_{0}^{5}{(x^{2} + 3)^{2}}dx$ $V = \int_{0}^{5}{(x^{2} + 3)^{2}}dx$. D. $V = \pi\int_{0}^{5}{(x^{2} + 3)\ }dx$ $V = \pi\int_{0}^{5}{(x^{2} + 3)\ }dx$.

Câu 8: Trong không gian $Oxyz$, cho hai điểm $A(5; - 4;2)$ và $B(1;2;4)$. Mặt phẳng đi qua $A$ và vuông góc với đường thẳng $AB$ là:

A. $2x - 3y - z - 20 = 0$. B. $3x - y + 3z - 25 = 0$.

C. $3x - y + 3z - 13 = 0$. D. $2x - 3y - z + 8 = 0$.

Câu 9: Tập nghiệm của bất phương trình $\log x \geq 1$ $\log x \geq 1$ là:

A. $\lbrack 10; + \infty).$ $\lbrack 10; + \infty).$ B. $(0; + \infty).$ $(0; + \infty).$ C. $(10; + \infty).$ $(10; + \infty).$ D. $( - \infty;10).$ $( - \infty;10).$

Câu 10: Cho hàm số $y = ax^{3} + 3x - d\ \ (a,d\mathbb{\in R})$ $y = ax^{3} + 3x - d\ \ (a,d\mathbb{\in R})$ có đồ thị là đường cong trong hình vẽ. Khẳng định nào dưới đây đúng?

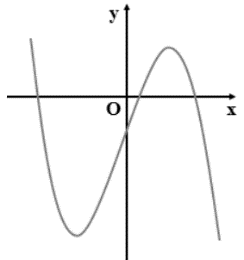
A. $a < 0,d > 0$ . B. $a < 0,d < 0$ . C. $a > 0,d < 0$ . D. $a > 0,d > 0$ .

Câu 11: Hàm số nào sau đây nghịch biến trên $\mathbb{R}$ $\mathbb{R}$?

A. $y = log_{\frac{1}{2}}x$ $y = log_{\frac{1}{2}}x$. B. $y = 3^{- x}$ $y = 3^{- x}$. C. $y = 2025^{x}$ $y = 2025^{x}$. D. $y = 2^{x}$ $y = 2^{x}$.

Câu 12: Cho cấp số nhân $(u_{n})$ $(u_{n})$ với $u_{1} = 3$ $u_{1} = 3$ và công bội $q = 2$. Giá trị của $u_{3}$ $u_{3}$ bằng

A. $12$. B. $18$. C. $7$. D. $6$.

PHẦN II. Câu trắc nghiệm đúng sai.

Câu 13: Một hộp có $26$chiếc thẻ cùng loại, mỗi thẻ được ghi một số trong các số $1,2,...,25,26$: hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Xét các biến cố:

$A$: “ Số trên thẻ được rút ra và là số chia hết cho $2$”.

$B$: “ Số trên thẻ được rút ra và là số chia hết cho $3$”.

$C$: “ Số trên thẻ được rút ra và là số chia hết cho $2$ hoặc chia hết cho $3$ ”.

$D$: “ Số trên thẻ được rút ra và là số chia hết cho $6$ hoặc $7$”.

a) Biến cố $A$ và biến cố $B$ là hai biến cố xung khắc.

b) Biến cố $C$ là biến cố giao của biến cố $A$và biến cố $B$.

c) $P(C) = \frac{17}{26}$ $P(C) = \frac{17}{26}$.

d) $P(D) = \frac{3}{20}$ $P(D) = \frac{3}{20}$.

Câu 14: Một cơ sở sản xuất khăn đang bán mỗi chiếc khăn với giá 50000 đồng một chiếc và mỗi tháng cơ sở bán được trung bình 34000 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhuận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 50000 đồng mà cứ tăng giá thêm 1000 đồng thì mỗi tháng sẽ bán ít hơn 500 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 32000 đồng, gọi số tiền cần tăng giá mỗi chiếc khăn là $x$ (nghìn đồng). Xét tính đúng sai của các khẳng định sau:

a) Tổng doanh thu trung bình mỗi tháng cơ sở sản xuất thu được khi chưa tăng giá là $1\ 700\ 000\ 000$ $1\ 700\ 000\ 000$ nghìn đồng.

b) Số khăn bán ra được mỗi tháng sau khi tăng giá là $34000 - 5x$ chiếc.

c) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi chiếc khăn lãi 41000đ.

d) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm $12500$ chiếc.

Câu 15: Một ô tô đang di chuyển với vận tốc $21m/s$, khi còn cách trạm thu phí một đoạn thì người lái xe bắt đầu đạp phanh lần một, xe chuyển động thẳng, chậm dần đều với vân tốc biến thiên theo thời gian được xác định bởi quy luật $v_{1}(t) = - 6t + 21\ (m/s)$ $v_{1}(t) = - 6t + 21\ (m/s)$, trong đó thời gian $t$ tính bằng giây, đến đúng trạm thu phí thì xe dừng hẳn. Sau khi trả phí, xe ô tô bắt đầu chuyển động nhanh dần đều với vận tốc $v_{2}(t) = 5t\ (m/s)$ $v_{2}(t) = 5t\ (m/s)$; đi được $4s$ ô tô gặp chướng ngại vật lên phải phanh gấp lần hai. Khi đó:

a) Quãng đường ô tô đi được từ lúc đạp phanh đến khi dừng ở trạm thu phí là $36,75m$.

b) Vận tốc của ô tô tại thời điểm người tài xế phanh gấp lần 2 là $20m/s$.

c) Thời gian kể từ lúc đạp phanh lần một cho đến khi dừng hẳn ở trạm thu phí là $3$ giây.

d) Tổng quãng đường ô tô chuyển động từ lúc phanh lần 1 đến phanh lần 2 là $76,75\ m$ $76,75\ m$.

Câu 16: Năm 2011, kỹ sư Nguyễn Trí Hiếu, người Quảng Ngãi, đã sáng chế ra chiếc xe đu dây phục vụ công nhân điện lực di chuyển trên dây điện cao thế. Khi ở vị trí cân bằng, chiếc xe và đường dây điện sẽ cùng nằm trên một mặt phẳng vuông góc với mặt đất. Xe được cấu tạo bởi khung xe có gắn hai Puly tại vị trí $A$ và $B$ cách mặt đất lần lượt là $20m$ và $19,9m$ (như hình). Xe đu dây di chuyển giống xe đạp, được kết hợp dây xích, líp, đĩa, bàn đạp, phanh...; bàn đạp đặt tại vị trí $C$.

Chọn hệ trục tọa độ $Oxyz$ sao cho mặt phẳng $(Oxy)$ trùng với mặt đất (mỗi đơn vị độ dài trong không gian $Oxyz$tương ứng với $1m$ trên thực tế); tọa độ các điểm $A;B;C$ lần lượt là $(7;5;20);\ \ (7;5,5;19,9);(7;5;19)$ $(7;5;20);\ \ (7;5,5;19,9);(7;5;19)$.

a) Một vectơ chỉ phương của đường thẳng $AB$ là $\overrightarrow{u} = (0;5;1)$ $\overrightarrow{u} = (0;5;1)$.

b) Khi người thợ điện di chuyển đến vị trí điểm $D$ cách mặt đất $18m$ thì tọa độ điểm $D$ là $D(7; - 5;18)$.

c) Phương trình mặt phẳng $(ABC)$ là $x = 7$.

d) Khoảng cách từ Puly tại $A$ đến bàn đạp tại $C$ là $1,03m$ (kết quả làm tròn đến hàng phần trăm).

PHẦN III. Câu trắc nghiệm trả lời ngắn.

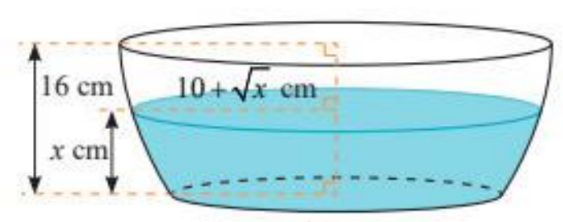
Câu 1: Nếu cắt chậu nước có hình dạng như hình bên bằng mặt phẳng song song và cách mặt đáy $x(cm)(0 \leq x \leq 16)$ $x(cm)(0 \leq x \leq 16)$ thì mặt cắt là hình tròn có bán kính $R = 10 + \sqrt{x}\ (cm)$ $R = 10 + \sqrt{x}\ (cm)$. Tìm $x$ (đơn vị cm, làm tròn kết quả đến hàng phần trăm) để dung tích nước trong chậu bằng $\frac{1}{2}$ $\frac{1}{2}$ thể tích của chậu?

Trả lời:

Câu 2: Cho hình chop đều $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a\sqrt{2}$ $a\sqrt{2}$, cạnh bên $SA = 2a$. Côsin của góc giữa hai mặt phẳng $(SDC)$ và $(SAC)$ bằng $\sqrt{\frac{b}{c}}$ $\sqrt{\frac{b}{c}}$ với phân số $\frac{b}{c}$ $\frac{b}{c}$ tối giản, $b > 0$, $c > 0$. Tính $T = b + 2c$.

Trả lời:

Câu 3: Một phần mềm mô phỏng vận động viên tập bắn bia mục tiêu có kích thước nhỏ $(42\ cm\ \times \ 42\ cm)$ $(42\ cm\ \times \ 42\ cm)$ trong không gian $Oxyz$ (giả sử $\left| \overrightarrow{i} \right| = \left| \overrightarrow{j} \right| = \left| \overrightarrow{k} \right| = 1\ cm$ $\left| \overrightarrow{i} \right| = \left| \overrightarrow{j} \right| = \left| \overrightarrow{k} \right| = 1\ cm$). Cho biết vận động viên đó sử dụng thước ngắm 3 và đứng cách xa bia mục tiêu là 100 m, trục $d$ của nòng súng và cọc đỡ bia $d'$ lần lượt có phương trình $d:\left\{ \begin{matrix} x = t \\ y = 2 \\ z = 4 \end{matrix} \right.$ $d:\left\{ \begin{matrix} x = t \\ y = 2 \\ z = 4 \end{matrix} \right.$ và $d':\left\{ \begin{matrix} x = 1 \\ y = 2 \\ z = 1 + 3t' \end{matrix} \right.$.

Để bắn trúng hồng tâm (thang điểm 10) thì vận động viên phải ngắm bắn vào điểm $N(a;b;c) \in d$ $N(a;b;c) \in d'$ và cách giao điểm của $d$ và $d'$ một khoảng 6 cm. Khi $c < 0$, tính giá trị biểu thức $2a - b + 3c$.

Trả lời:

Câu 4: Cho các chữ số $0;2;3;4;5;7;8$. Từ các chữ số đó có thể lập được bao nhiêu số có 4 chữ số khác nhau chia hết cho $20$ và luôn xuất hiện chữ số $4.$

Trả lời:

Câu 5: Một doanh nghiệp dự định sản xuất không quá 400 sản phẩm. Nếu doanh nghiệp sản xuất $x$ sản phẩm $(1 \leq x \leq 400)$ $(1 \leq x \leq 400)$ thì doanh thu nhận được khi bán hết số sản phẩm đó là $F(x) = x^{3} - 1999x^{2} + 1001000x + 250000$ $F(x) = x^{3} - 1999x^{2} + 1001000x + 250000$ (đồng). Trong đó chi phí vận hành máy móc cho mỗi sản phẩm là $G(x) = \frac{200000x}{3x + 2}$ $G(x) = \frac{200000x}{3x + 2}$ (đồng). Tổng chi phi mua nguyên vật liệu là $H(x) = 2x^{3} + 100000x - 50000$ $H(x) = 2x^{3} + 100000x - 50000$ (đồng), nhưng do doanh nghiệp đó mua nguyên vật liệu với số lượng lớn nên được giảm $2\%$ $2\%$ cho 150 sản phẩm đầu tiên doanh nghiệp sản xuất và giảm $3\%$ $3\%$ cho các sản phẩm tiếp theo. Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?

Trả lời:

Câu 6: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$, cạnh bên bằng $3a$. Khoảng cách từ điểm $A$ đến mặt phẳng $(SCD)$ bằng $a\sqrt{\frac{b}{c}}$ $a\sqrt{\frac{b}{c}}$ , với phân số $\frac{b}{c}$ $\frac{b}{c}$ tối giản, $b > 0,\ \ c > 0$ $b > 0,\ \ c > 0$. Tính $T = 3c + 2b$.

Trả lời:

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

Tải về

Chọn file muốn tải về: