Đề thi thử tốt nghiệp THPT 2025 môn Toán bám sát đề minh họa - Đề 60
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
BÁM SÁT ĐỀ MINH HỌA
ĐỀ 60
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2025
MÔN: TOÁN
Thời gian làm bài 90 phút; không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số
( ) 2
x
fx
là:
A.
1
2
1
x
C
x
. B.
2
ln2
x
C
. C.
2
x
C
x
. D.
1
.2
x
xC
.
Câu 2: Gọi
D
là hình phẳng giới hạn bởi các đường
3
, 0, 0y x y x
và
1x
. Thể tích của khối tròn
xoay tạo thành khi quay
D
quanh trục
Ox
bằng
A.
1
3
0
dxx
. B.
1
3
0
2dxx
.
C.
1
6
0
dxx
. D.
1
6
0
x dx
.
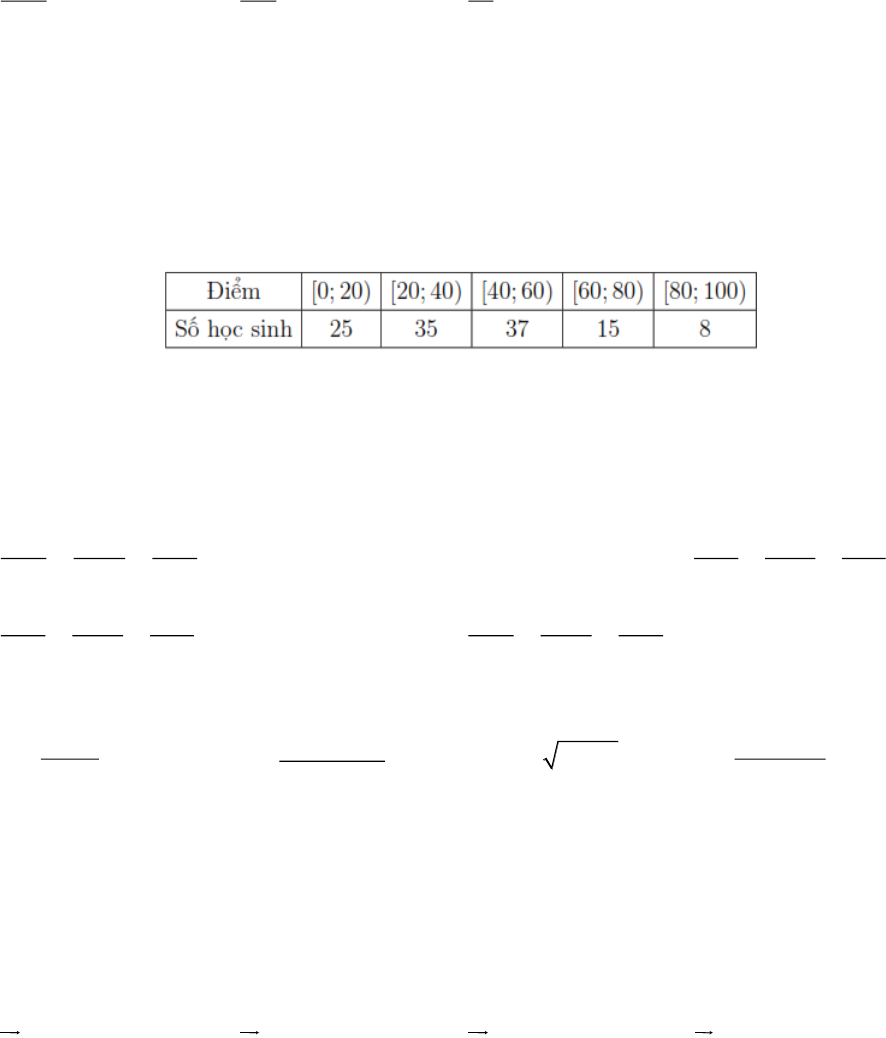
Câu 3: Thống kê điểm thi đánh giá năng lực của một trường THPT qua thang điểm 100 được cho ở bảng sau:
Trung vị của mẫu số liệu ghép nhóm thuộc khoảng nào sau đây?
A.
0;20
. B.
20;40
. C.
40;60
. D.
60;80
.
Câu 4: Trong không gian
Oxyz
, phương trình của đường thẳng đi qua
1;2;1M
và
3;1; 2N
là
A.
1 2 1
.
4 3 1
x y z
B.
1 2 1
2 1 3
x y z
.
C.
1 2 1
4 3 1
x y z
. D.
1 2 1
2 1 3
x y z
.
Câu 5: Trong các hàm số sau đây, hàm số nào có đồ thị nhận đường thẳng
1x
làm đường tiệm cận đứng?
A.
21
1
x
y
x
. B.
2
23
23
xx
y
x
. C.
2
2y x x
. D.
2
2
1
y
xx
.
Câu 6: Tập nghiệm của bất phương trình
2
3
2log 18 x
là:
A.
3S
. B.
3S
. C.
3S
. D.
4;3S
.
Câu 7: Trong không gian
Oxyz
, cho mặt phẳng
: 2 5 0P x y z
. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
P
?
A.
4
1; 2;1n
. B.
3
1;2;1n
. C.
2
1; 2; 5n
. D.
1
1; 2; 1n
.
Câu 8: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật và
SA ABCD
. Đường thẳng CD vuông
góc với mặt phẳng nào sau đây?
A.
SAB
. B.
SBC
. C.
SAC
. D.
SAD
.
Câu 9: Nghiệm phương trình
3
log 2x
là
A.
3x
. B.
6x
. C.
8x
. D.
9x
.
Câu 10: Cho cấp số cộng
n
u
có
25
5, 17uu
. Công sai
d
của cấp số cộng là:
A. 1. B. 2. C. 8. D. 4.
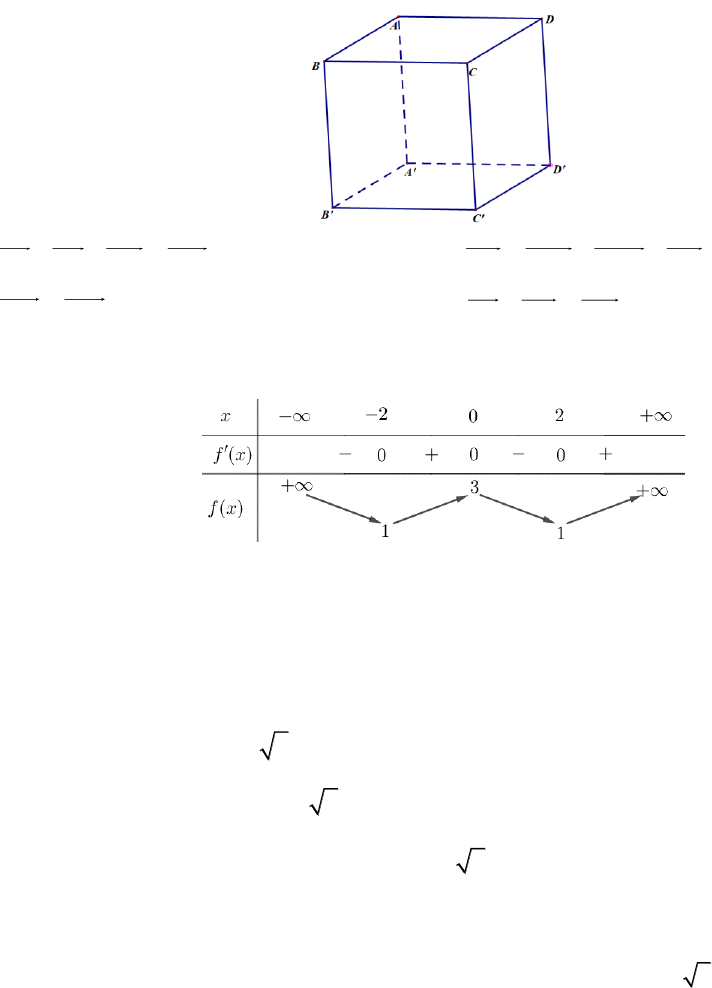
Câu 11: Cho hình lập phương
.ABCD ABC D
. Khẳng định nào sai trong các khẳng định sau
A.
''BA BC BB BD
. B.
' ' ' 'AC A B A D AA
.
C.
''BC AD
. D.
'AB AA AB
.
Câu 12: Cho hàm số
fx
có bảng biến thiên như sau:
Hàm số đã cho có điểm cực đại là
A.
(0;3)
. B.
0x
. C.
3y
. D.
1y
.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc
sai.
Câu 1: Cho hàm số
( ) 2cos 2f x x x
.
a) Tính
(0) 2f
và
22f
.
b) Đạo hàm của hàm số đã cho là
( ) 2sin 2f x x
.
c) Phương trình
( ) 0fx
có đúng 2 nghiệm trên đoạn
0;
.
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của
fx
trên đoạn
0;
là
2
.
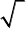
Câu 2: Trong không gian
Oxyz
, cho đường thẳng
1
: 2 2
32
xt
yt
zt
và mặt cầu
22
2
: 3 2 25S x y z
. Gọi
I
là tâm của mặt cầu
()S
.
a) Mặt cầu
S
có tâm
3;0; 2I
và bán kính
5R
.
b) Đường thẳng
đi qua điểm
2; 4; 6M
.
c) Hình chiếu vuông góc của tâm
I
lên đường thẳng
là điểm
1;2; 1H
.
d) Đường thẳng
cắt mặt cầu
()S
tại hai điểm
,AB
và diện tích
IAB
bằng
12
.
Câu 3: Một công trình xây dựng dự kiến hoàn thành trong
100
ngày. Gọi
Mt
là số ngày công được tính
đến hết ngày thứ
t
(kể từ khi khởi công công trình). Trong kinh tế xây dựng, người ta đã biết rằng
M t m t
với
mt
là số lượng công nhân được sử dụng tại thời điểm
t
. Biết rằng
100 12 2m t t t
(với
0 100t
).
a) Có
116
công nhân được sử dụng vào ngày thứ
4
.
b) Số công nhân được sử dụng nhiều nhất vào ngày thứ
10
.
c) Trong
16
ngày đầu tiên, công trình đã cần
1856
ngày công.
d) Giả sử số tiền trả cho
1
ngày công là 500.000 đồng. Khi đó tổng số tiền phải trả cho nhân công để
hoàn thành công trình xây dựng đó theo thời gian dự kiến là 4 tỉ đồng.
Câu 4: Một căn bệnh X có
4%
dân số mắc phải. Một phương pháp chẩn đoán bệnh X có tỉ lệ chính xác là
99%
. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính
99%
số trường hợp.
Với những người không mắc bệnh, phương pháp này cũng chẩn đoán đúng
98%
. Chọn ngẫu nhiên
một người đi kiểm tra bệnh X bằng phương pháp trên.
a) Xác suất để người đó mắc bệnh khi chưa kiểm tra là
0,04
.
b) Xác suất kết quả dương tính nếu người đó không mắc bệnh là
0,01
.
c) Xác suất để người đó có kết quả dương tính là
0,0588
.
d) Biết rằng đã có kết quả chẩn đoán là dương tính, xác suất để người đó thực sự mắc bệnh là
0,6
.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật cạnh
22AB AD
. Tam giác
SAB
đều và nằm
trong mặt phẳng vuông góc với đáy
ABCD
. Tính khoảng cách từ
A
đến mặt phẳng
SBD
(làm
tròn kết quả đến chữ số thập phân thứ hai)
Câu 2: Trong một trò chơi, người chơi muốn tìm đường đi ngắn nhất để đi từ A đến P, biết từ A đến P có
những đường đi như hình vẽ và khoảng cách giữa các vị trí được cho trên hình. Đường đi thoả mãn
điều kiện trên nhận giá trị nhỏ nhất là bao nhiêu?
Đề thi thử bám sát đề minh họa 2025 môn Toán - Đề 60
VnDoc.com xin gửi tới bạn đọc bài viết Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán bám sát đề minh họa - Đề 60 có đáp án để bạn đọc cùng tham khảo. Đề thi được biên soạn theo cấu trúc đề thi mới. Đề thi được tổng hợp gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi đúng sai và 6 câu hỏi trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi bài viết dưới đây để có thêm tài liệu ôn thi kì thi tốt nghiệp THPT Quốc gia sắp tới nhé.


