Đề thi thử THPT Quốc gia môn Toán - Đề 2
Luyện đề thi THPT Quốc gia môn Toán
Để chuẩn bị hiệu quả cho kỳ Thi THPT Quốc gia năm 2025 - 2026, việc luyện tập với các đề thi thử môn Toán có đáp án là bước quan trọng giúp học sinh đánh giá năng lực, rèn kỹ năng xử lý câu hỏi trắc nghiệm và nâng cao tốc độ làm bài. Bài viết này giới thiệu Đề thi thử THPT Quốc gia môn Toán – Đề 2, được biên soạn bám sát cấu trúc đề minh họa, đi kèm đáp án để bạn dễ dàng tự kiểm tra và củng cố kiến thức. Đây là tài liệu cần thiết giúp bạn tăng tốc hiệu quả trong giai đoạn ôn luyện.
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2025 – 2026
ĐỀ ÔN TẬP SỐ 2
THỜI GIAN: 90 PHÚT. NGÀY … /…/2026
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nghiệm của phương trình 
\(log_{2}x =
3\) là
A. \(x = 5\) B. \(x = 8\). C. \(x =
6\). D. \(x = 9\)
Câu 2: Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow{u} =
2\overrightarrow{i} - 5\overrightarrow{k}\). Tọa độ của vectơ \(\overrightarrow{u}\) là
A. \((0;2; - 5).\) B. \((2;0;5).\) C. \((2; - 5;0).\) D. \((2;0; - 5).\)
Câu 3: Trong không gian \(Oxyz\), cho hai điểm \(A( - 1;2;1)\) và\(B(2;1; - 3)\). Tọa độ của vectơ \(\overrightarrow{AB}\) là
A. \(\left( \frac{1}{2};\frac{3}{2}; - 1
\right)\) B. \(( - 3;1;4).\) C. \((3; - 1; - 4).\) D. \((1;3; - 2).\)
Câu 4: Nguyên hàm của hàm số \(f(x) = \sin
x\) là
A. \(\cos x + C\). B. \(\frac{sin^{2}x}{2} + C\) C. \(- \cos x + C\). D. \(\sin x + C\).
Câu 5: Giá trị nhỏ nhất của hàm số \(y =
x^{4} - 4x^{2} + 3\) trên đoạn \(\lbrack 0;4\rbrack\) là
A. \(0\). B. \(\sqrt{2}\). C. \(3\). D. \(-
1\).
Câu 6: Một hộp đựng \(9\) tấm thẻ cùng loại được ghi số thứ tự từ \(1\) đến \(9\). Rút ngẫu nhiên đồng thời hai tấm thẻ trong hộp. Xác suất để rút được cả hai tấm thẻ cùng ghi số chẳn là.
A. \(\frac{1}{2}\). B. \(\frac{1}{3}\). C. \(\frac{5}{6}\). D. \(\frac{1}{6}\).
Câu 7: Cấp số nhân \((u_{n})\) có \(u_{1} = 2\) và \(u_{2} = 6\). Số hạng \(u_{4}\) của cấp số nhân là:
A. \(27\). B. \(162\). C. \(54\). D. \(11\).
Câu 8: Tập nghiệm của bất phương trình \(log_{\frac{1}{2}}(x + 1) \leq log_{\frac{1}{2}}(2x
- 1)\) là
A. \(\left( \frac{1}{2};2
\right\rbrack\). B. \(\left(
\frac{1}{2};2 \right)\). C. \(( - \infty;2).\) D. \(( - \infty;2\rbrack\).
Câu 9: Thể tích của khối chóp có diện tích đáy bằng \(S\), chiều cao bằng \(h\) là
A. \(V = \frac{1}{2}S.h\). B. \(V = \frac{1}{3}S.h\). C. \(V = S.h\). D. \(V = \frac{2}{3}S.h\).
Câu 10: Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ dưới đây.
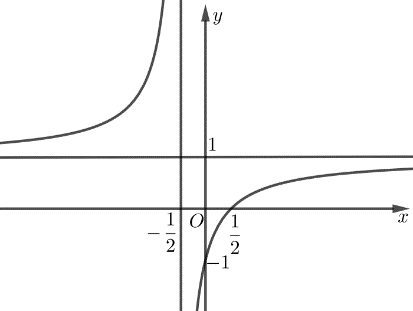
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình:
A. \(x = 1\). B. \(y = 1\). C. \(x = - \frac{1}{2}\). D. \(y = - \frac{1}{2}\).
Câu 11: Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ dưới đây.
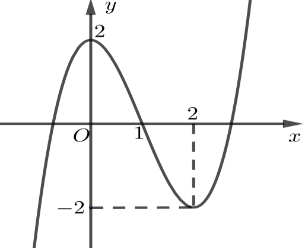
Hàm số đã cho đồng biến trên khoảng:
A. \((2; + \infty).\) B. \((0;2).\) C. \((1; + \infty)\). D. \(( - \infty;1)\).
Câu 12: Gọi \(F(x)\) là một nguyên hàm của hàm số \(f(x) = 2x -
\frac{1}{x}\) thoả mãn \(F(1) =
1\). Tính\(F( - 1)\).
A. \(F( - 1) = 1\). B. \(F( - 1) = 2\). C. \(F( - 1) = - 1\). D. \(F( - 1) = 0\).
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 13: Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
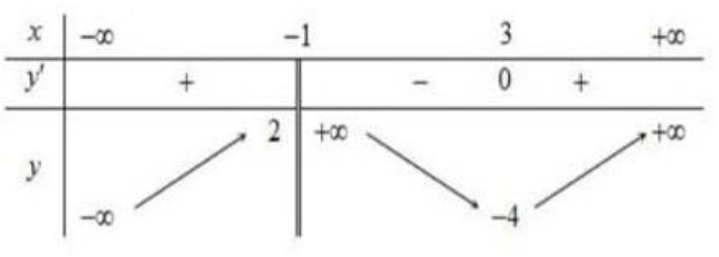
a) Đồ thị hàm số \(y = f(x)\) có đúng hai đường tiệm cận.
b) Hàm số \(y = f(x)\) đồng biến trên khoảng \((3; + \infty)\).
c) Hàm số \(y = f(x)\) có đúng một điểm cực trị.
d) Giá trị nhỏ nhất của \(h(x) = 2f(x) +
2025x\) trên đoạn \(\lbrack
3;2025\rbrack\) bằng \(6083\).
Câu 14: Trong không gian \(Oxyz\) cho \(3\) điểm \(A(2, - 1,1)\),\(B( - 1,3, - 1)\) , \(C(5; - 3,4)\)
a) Tích vô hướng của hai vectơ \(\overrightarrow{AB}.\overrightarrow{AC} = -
23\)
b) Góc \(\widehat{BAC}\) là góc nhọn.
c) Côsin của góc giữa hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) bằng \(\frac{- 23}{\sqrt{638}}\).
d) Lấy điểm \(M \in (Oxy)\) sao cho \(MA^{2} + MB^{2} + MC^{2}\) đạt giá trị nhỏ nhất, khi đó tọa độ điểm\(M \in \left(
2; - \frac{1}{3};0 \right).\)
Câu 15: Xét phương trình \(2sin3x - 1 =
0\)
a) Tập nghiệm của phương trình là \(S =
\left\{ \frac{\pi}{18} + \frac{k2\pi}{3};\ \frac{5\pi}{18} +
\frac{k2\pi}{3}/\ k\mathbb{\in Z} \right\}\).
b) Nghiệm dương nhỏ nhất của phương trình là \(x = \frac{\pi}{18}\).
c) Phương trình có đúng \(3\) nghiệm trên \(\lbrack 0;\ \pi\rbrack\).
d) Tổng các nghiệm của phương trình thuộc đoạn \(\lbrack 0;\ \pi\rbrack\) bằng \(2\pi\).
Câu 16: Cho hàm số \(f(x) = \frac{2x +
1}{x}\).
a) \(\int_{}^{}{f(x)}dx = 2x + \ln|x| +
C\).
b) Gọi \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) và thỏa mãn \(F(1) = 3\). Khi đó \(F(x) = 2x + \ln|x| + 1\).
c) \(\int_{}^{}{f'(2x)}dx = \frac{-
1}{4x} + C\).
d) Gọi \(G(x)\) là một nguyên hàm của hàm số \(f(x)\). Biết \(G(2) = 1\) và \(G(5) + G( - 5) = 0\). Tìm được \(G( - 10) = aln10 + bln5 + cln2 + d\), với \(a,\ b,\ c\) là các số hữu tỷ. Khi đó\(a + b + c + d = - 19\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1: Hình vẽ dưới đây cho biết một miền \(D\) (được tô đậm) nằm trong hình vuông cạnh bằng \(4\), miền \(D\) này gồm những điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới cạnh gần nhất của hình vuông. Tính diện tích miền \(D\), với kết quả làm tròn đến chữ số thập phân thứ nhất.
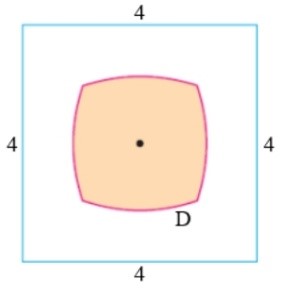
Trả lời:
Câu 2: Một thầy giáo có 16 cuốn sách khác nhau gồm 4 cuốn sách Toán, 5 cuốn sách Lý và 7 cuốn sách Hóa. Thầy lấy ra ngẫu nhiên 8 cuốn sách để tặng cho học sinh. Tính xác suất để số sách còn lại của thầy có đủ cả ba môn ( làm tròn kết quả đến hàng phần trăm).
Trả lời:
Câu 3: Năm 2025, một cửa hàng cần nhập về tổng cộng 600 chiếc điện thoại. Cửa hàng sẽ nhận theo nhiều lô hàng, mỗi lô hàng chứa số điện thoại bằng nhau. Chi phí vận chuyển là 50 USD cho mỗi lô hàng, cộng thêm một loại phí vận chuyển là 3 USD cho mỗi chiếc điện thoại và phí này cả năm chỉ tính cho lần vận chuyển đầu tiên. Hỏi cửa hàng đó nên nhập mỗi lô hàng bao nhiêu chiếc điện thoại để chi phí vận chuyển cả năm 2025 thấp nhất?
Trả lời:
Câu 4: Xét trong không gian \(Oxyz\), đài kiểm soát không lưu sân bay đặt ở gốc toạ độ \(O(0;0;0).\), đơn vị trên mỗi trục là ki-lô-mét. Một máy bay chuyển động theo đường thẳng, bay qua hai vị trí \(A( - 500; - 300;500)\) và. Khi máy bay ở gần đài kiểm soát không lưu nhất, toạ độ máy bay là \((a;b;c)\). Tính giá trị của biểu thức \(P = a + b + c\).
Trả lời:
Câu 5: Cho hình chóp \(S.ABC\) có đáy\(ABC,SAB\) là các tam giác đều và mặt bên \((SAB)\)vuông góc với mặt đáy. Gọi \(\alpha\) là số đo của góc phẳng nhị diện \(\lbrack S,BC,A\rbrack\). Tính \(cos^{2}\alpha\).
Trả lời:
Câu 6: Trong môi trường giới hạn, số lượng một loài sinh vật được cho bởi công thức \(P(t) = \frac{100000}{1 + 4^{-
t}}\) , trong đó thời gian \(t\) tính theo đơn vị năm. Tính thời gian cần thiết (đơn vị năm) để số lượng loài sinh vật đó đạt \(80000\) (kết quả làm tròn đến hàng phần trăm).
Trả lời:
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
