Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chu Văn An, Hà Nội

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chu Văn An, Hà Nội là đề thi thử đại học môn Toán có đáp án mà VnDoc.com xin gửi tới các bạn tham khảo và nghiên cứu, chuẩn bị ôn tập tốt nhất cho kì thi Quốc gia đang tới rất gần. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Hà, Hải Dương (Lần 3)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Sư phạm Hà Nội (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Cao Bằng

SỞ GD & ĐT HÀ NỘI TRƯỜNG THPT CHU VĂN AN ĐỀ THI THỬ

ĐỀ THI THPT QUỐC GIA NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút

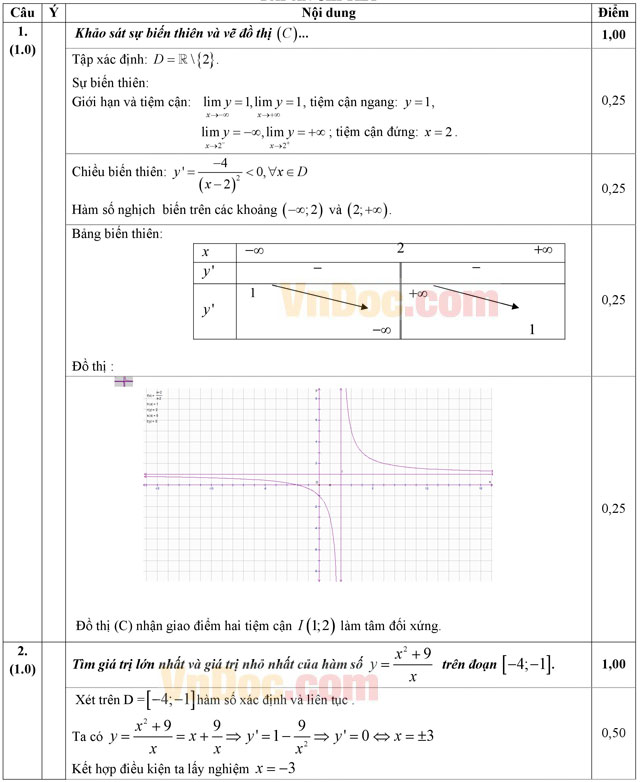
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số .

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-4; -1].

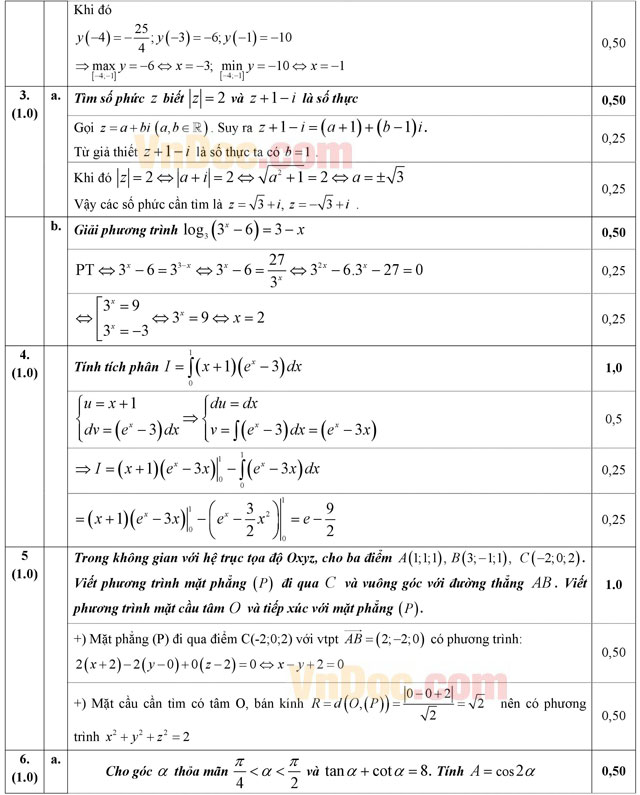
Câu 3 (1,0 điểm).

a. Tìm số phức z biết |z| = 2 và z + 1 - i là số thực;

b. Giải phương trình log₃(3^x - 6) = 3 - x.

Câu 4 (1,0 điểm). Tính tích phân .

Câu 5 (1,0 điểm). Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1; 1; 1), B(3; -1; 1), C(-2; 0; 2). Viết phương trình mặt phẳng (P) đi qua C và vuông góc với đường thẳng AB. Viết phương trình mặt cầu tâm O và tiếp xúc với mặt phẳng (P).

Câu 6 (1,0 điểm).

a) Cho góc α thỏa mãn π/4 < α < π/2 và tanα + cotα = 8. Tính A = cos2α.

b) Trong một đợt kiểm tra về độ an toàn nguồn nước ven biển ở các Tỉnh miền trung. Bộ y tế lấy ra 15 mẫu nước ven biển trong đó có 4 mẫu ở Hà Tĩnh, 5 mẫu ở Quảng Bình và 6 mẫu ở Thừa Thiên Huế. Mỗi mẫu nước này có thể tích như nhau và để trong các hộp kín có kích thước giống hệt nhau. Đoàn kiểm tra lấy ra ngẫu nhiên bốn hộp để phân tích, kiểm tra xem trong nước có bị nhiễm độc hay không. Tính xác suất để bốn hộp lấy ra có đủ ba loại nước ở cả ba Tỉnh.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc cạnh AD sao cho HD = 2HA. Gọi M, N lần lượt là trung điểm của SB, BC, biết góc giữa SB và mặt phẳng (ABCD) bằng 30^o. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng MN, SD.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình thang cân ABCD có AD // BC. Phương trình đường thẳng chứa các cạnh AB, AC lần lượt là x - 2y + 3 = 0, y - 2 = 0. Gọi I là giao điểm của AC, BD. Tìm tọa độ các đỉnh hình thang ABCD biết IB = √2IA, hoành độ của I lớn hơn -3 và điểm M(-1; 3) thuộc đường thẳng BD.

Câu 9 (1,0 điểm). Giải bất phương trình sau trên tập R:

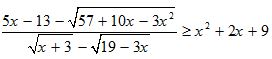
Câu 10 (1,0 điểm). Cho x, y là các số thực thỏa mãn điều kiện .

Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức:

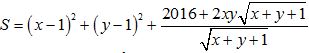
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016