Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 3)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 3) có đáp án là tài liệu ôn thi môn Toán chuẩn bị cho kì thi THPT Quốc gia hữu ích dành cho các bạn. Đề thi có đáp án đi kèm, giúp các bạn luyện thi đại học môn Toán hiệu quả. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 2)

SỞ GD&ĐT HẢI DƯƠNG TRƯỜNG THPT ĐOÀN THƯỢNG

ĐỀ THI THỬ THPT QUỐC GIA LẦN 3 NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút

Câu 1 (2,0 điểm) Cho hàm số y = -x³ + 2x² + 3.

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Biện luận theo m số nghiệm của phương trình x³ - 2x² + m = 0.

Câu 2 (1,0 điểm)

1. Tính môđun của số phức .
2. Giải bất phương trình 4^x > 2^x+1 + 3.

Câu 3 (1,0 điểm) Tính tích phân .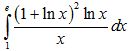

Câu 4 (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 0; -1) và đường thẳng . Viết phương trình mặt phẳng qua A và vuông góc với d. Tìm tọa độ điểm A' đối xứng với A qua đường thẳng d.

Câu 5 (1,0 điểm)

1. Giải phương trình 1 + 2cos2x = sin2x.
2. Vòng chung kết Euro 2016 có 24 đội bóng tham dự, trong đó có các đội Anh, Pháp, Đức, Italia và Tây Ban Nha. Ban tổ chức chọn ngẫu nhiên 2 đội bóng để đá trận khai mạc. Tính xác xuất để ít nhất một trong 5 đội bóng kể trên được đá trận khai mạc.

Câu 6 (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = a√3. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Góc giữa SD và mặt phẳng (ABCD) bằng 60⁰. Gọi M là trung điểm của SA. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ điểm C đến mặt phẳng (BDM).

Câu 7 (1,0 điểm) Giải hệ phương trình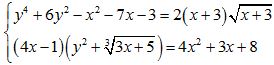

Câu 8 (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm H(-3; 1) là hình chiếu vuông góc của A trên BD. Điểm M(1/2; 2) là trung điểm cạnh BC, phương trình đường trung tuyến kẻ từ đỉnh A của tam giác ADH là d: 4x + y + 13 = 0. Viết phương trình đường thẳng BC.

Câu 9 (1,0 điểm) Cho và không có hai số nào đồng thời bằng 0. Tìm giá trị nhỏ nhất của biểu thức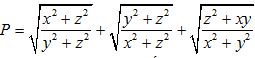

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán