Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Hà, Hải Dương (Lần 3)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Hà, Hải Dương (Lần 3) được VnDoc.com sưu tầm và đăng tải, là đề luyện thi THPT Quốc gia, ôn thi Đại học môn Toán hữu ích dành cho các bạn thí sinh. Đề thi có 10 câu hỏi cùng đáp án đi kèm, giúp các bạn kiểm tra lại bài làm của mình một cách hiệu quả.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Hà, Hải Dương (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Liên Hà, Hà Nội

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

SỞ GIÁO DỤC & ĐÀO TẠO HẢI DƯƠNG Trường THPT Thanh Hà ĐỀ CHÍNH THỨC

ĐỀ THI THỬ THPT QUỐC GIA LẦN 3 Năm học 2015 – 2016. Môn Toán, Khối 12. Thời gian làm bài 180 phút

Câu 1 (1,0 điểm): Khảo sát sự biến thiên và vẽ đồ thị hàm số .

Câu 2 (1,0 điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = e^2x(2x + 3) trên đoạn [-3; 0].

Câu 3 (1,0 điểm):

a) Cho sinα = 3/5 với π/2 < α < π. Tính giá trị biểu thức: .

b) Giải phương trình: .

Câu 4 (1,0 điểm):

a) Gọi z₁, z₂ là các nghiệm phức của phương trình z² - 2z + 5 = 0. Tính độ dài đoạn AB, biết A, B lần lượt là các điểm biểu diễn số phức z₁, z₂.

b) Cho phép khai triển thành biểu thức ẩn x. Tìm số hạng không chứa x.

Câu 5 (1,0 điểm): Tính diện tích hình phẳng (H) giới hạn bởi các đường: y = 2xe^x, y = 0, x = 2.

Câu 6 (1,0 điểm): Cho lăng trụ tam giác đều ABC.A'B'C' có góc giữa BC' và mặt phẳng (ABB'A') là 30^o, cạnh đáy là a√3. Tính thể tích khối lăng trụ ABC.A'B'C' và khoảng cách giữa hai đường BC' và AC.

Câu 7 (1,0 điểm): Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;3) và đường thẳng d có phương trình . Viết phương trình mặt phẳng (P) qua A và vuông góc với d. Tìm tọa độ điểm M thuộc d sao cho AM = 2√6.

Câu 8 (1,0 điểm): Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC nội tiếp đường tròn (C) có phương trình: x² + y² + 2x - 4 y - 20 = 0. Đường cao kẻ từ đỉnh A của tam giác ABC cắt (C) tại E(3;-1) khác A. Điểm G(5/3; 5/3) là trọng tâm tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC biết đỉnh B có hoành độ lớn hơn 3.

Câu 9 (1,0 điểm): Giải hệ phương trình: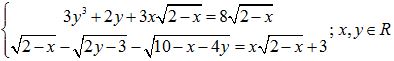

Câu 10 (1,0 điểm): Cho a, b, c là các số thực dương thỏa mãn: a³ + b³ + c³ = 3.

Chứng minh .

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016