Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Trần Đại Nghĩa
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Trần Đại Nghĩa là đề thi thử Quốc gia năm 2015 môn Toán có đáp án. Tài liệu này giúp các bạn tự luyện tập, ôn luyện lại kiếm thức đã học, nhằm chuẩn bị tốt nhất cho các kì thi quan trọng sắp tới. Mời các bạn tham khảo.
Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Thủ Đức, TP. Hồ Chí Minh
Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Bạch Đằng, Hải Phòng
| Trường THPT Trần Đại Nghĩa Tổ Toán |
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1 NĂM 2015 MÔN TOÁN Thời gian: 180 phút (không kể thời gian phát đề) |
Câu 1: (2 điểm)
- Khảo sát và vẽ đồ thị (C) của hàm số y = x3 - 3x - 2
- Tìm tọa độ của điểm M trên (C) sao cho tiếp tuyến của (C) tại M song song với đường thẳng (d): 9x - y - 18 = 0
Câu 2:
a/ (0,5 điểm) Giải phương trình sau log3(2x - 1) - 4log9(5x + 2) + 4 = 0
b/ (0.5 điểm) Giải phương trình cos3x + 2 sin2x – cosx = 0
| Câu 3: (1 điểm) Tính tích phân | 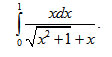 |
Câu 4:
a/ (0.5 điểm) Tìm giá trị lớn nhất và nhỏ nhất của hàm số
b/ (0.5 điểm) Biết trong số 10 vé xổ số còn lại trên bàn vé có 2 vé trúng thưởng. Khi đó một người khách rút ngẫu nhiên 5 vé. Hãy tính xác suất sao cho trong 5 vé được rút ra có ít nhất một vé trúng thưởng.
Câu 5: (1 điểm) Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, mặt bên (SAB) nằm trong mặt phẳng vuông góc với đáy (ABCD), tam giác SAB vuông tại S, SA = a Hãy tính thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB, SC theo a
Câu 6: (1 điểm) Trong không gian Oxyz cho mặt phẳng (P): 2x - 2y + z - 1 = 0 và điểm A(1; -1; 0)
a/ Hãy viết phương trình mp (α) qua điểm A và song song với mặt phẳng (P)
b/ Tìm tọa độ điềm M thuộc mp (P) sao cho MA vuông góc với mp (P)
Câu 7: (1 điểm) Trong mặt phẳng Oxy cho hình vuông ABCD có đường chéo AC phương trình là x + y - 10 = 0. Tìm tọa độ điểm B biết rằng đường thẳng CD qua điểm M(6; 2) và đường thẳng AB qua điểm N(5; 8)
| Câu 8: (1 điểm) Giải hệ phương trình | { | x2 + xy + y2 = 7 |
| x2 - xy - 2y2 = -x + 2y |
Câu 9: (1 điểm) Cho các số thực không âm x, y thỏa mãn x2 + y2 + (3x - 2)(y - 1) = 0
Tìm giá trị lớn nhất của biểu thức ![]()
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1 (2 điểm)
a. 1 điểm
- TXĐ: D = r
- y' = 3x2 - 3
- y' = 0 => x = 1 hoặc x = -1
![]()
- BBT: Đúng chiều biến thiên
Đúng các giới hạn và cực trị
- KL: Hs đồng biến trong khoảng (-∞;-1) và (1; +∞); nghịch biến trong khoảng (-1; 1); đạt cực đại bằng 0 tại x = -1; đạt cực tiểu bằng -4 tại x = 1
- Điểm đặc biệt: đồ thị hàm số cắt trục hoành tại các điểm (2; 0) và (-1;0) có điểm uốn (0; 2)
- Đồ thị: Vẽ đúng đồ thị qua các điểm cực trị, điểm đặc biệt và đúng dạng.
b. 1 điểm
- Đường thẳng 9x – y – 18 = 0 có hệ số góc bằng 9
- Gọi M0(x0; y0) là điểm mà tại đó tiếp tuyến song song đường thẳng
9x - y - 18 = 0 => f'(x0) = 9 => 3x02 - 3 = 9 <=> x0 = 2 hoặc x0 = -2
- Với x0 = 2 → y0 = 0 →M0( 2; 0)
x0 = -2 → y0 = -4 → M0( -2 ; -4 )
- Kiểm tra lại
M0(2;0) tiếp tuyến tại M0 có pt là y = 9(x – 2) ↔ 9x - y - 18 = 0 (loại)
M0(-2;-4) tiếp tuyến tại M0 có pt là y = 9(x + 2) - 4 ↔ 9x - y + 14 = 0 (nhận)
Câu 2 ( 1 điểm)
a. 0,5 điểm
- Đk: x > 1/2
log3(2x - 1) - 4log9(5x + 2) + 4 = 0
<=> log3(2x - 1) - 2log3(5x + 2) = -4
<=> log3(2x - 1) - log3(5x + 2)2 = -4
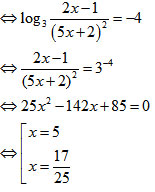
So với đk ta nhận x = 5 và x = 17/25.


