Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Bạch Đằng, Hải Phòng

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Bạch Đằng, Hải Phòng là đề thi thử đại học môn Toán có đáp án chi tiết, giúp các bạn ôn tập lại kiến thức, luyện thi đại học môn Toán hiệu quả, chuẩn bị cho kì thi THPT Quốc gia môn Toán được tốt nhất.

Đề thi thử THPT Quốc gia lần 1 năm 2015 môn Toán trường THPT Chuyên Võ Nguyên Giáp, Quảng Bình

Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Lương Ngọc Quyến

SỞ GD&ĐT HẢI PHÒNG TRƯỜNG THPT BẠCH ĐẰNG

ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian giao đề

Câu 1 (2,0 điểm). Cho hàm số y = -x³ + 3mx + 1 (1).

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1.

b) Tìm m để đồ thị của hàm số (1) có 2 điểm cực trị A, B sao cho tam giác OAB vuông tại (O) (với O là gốc tọa độ).

Câu 2 (1,0 điểm). Giải phương trình: sin2x + 1 = 6sinx + cos2x.

Câu 3 (1,0 điểm). Tính tích phân: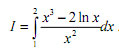

Câu 4 (1,0 điểm).

a) Giải phương trình 5^2x+1 - 6.5^x + 1 = 0.

b) Một tổ có 5 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh để làm trực nhật. Tính xác suất để 3 học sinh được chọn có cả nam và nữ.

Câu 5 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho điểm (-4;1;3) và đường thẳng d: (x + 1)/-2 = (y - 1)/1 = (z + 3)/3. Viết phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng d. Tìm tọa độ điểm B thuộc d sao cho AB = √27.

Câu 6 (1,0 điểm). Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với đáy 1 góc bằng 60⁰. Tính thể tích khối chóp S.ABC và tính khoảng cách từ điểm I đến mặt phẳng (SAB) theo a.

Câu 7 (1,0 điểm). Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC có A(1;4), tiếp tuyến tại A của đường tròn ngoại tiếp tam giác ABC cắt BC tại D, đường phân giác trong của góc ADB có phương trình x - y + 2 = 0, điểm M(-4;1) thuộc cạnh AC. Viết phương trình đường thẳng AB.

Câu 8 (1,0 điểm). Giải hệ phương trình

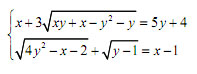
Câu 9 (1,0 điểm). Cho a, b, c là các số dương và a + b + c = 3. Tìm giá trị lớn nhất của biểu thức:

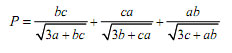
Đá án đề thi thử THPT Quốc gia môn Toán

Câu 1 (2,0 điểm)

a. 1,0 điểm

Với m = 1 hàm số trở thành: y = -x³ + 3x + 1

TXĐ: D = R

y' = -3x² + 3, y' = 0 ↔ x = ±1

Hàm số nghịch biến trên các khoảng (-∞; -1) và (1; +∞), đồng biến trên khoảng (-1; 1)

Hàm số đạt cực đại tại x = 1, y_CD = 3, đạt cực tiểu tại x = -1, y_CT = -1.

lim y	= +∞	lim y	= -∞
x→-∞		x→+∞

Bảng biến thiên

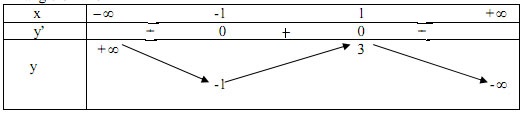
Đồ thị

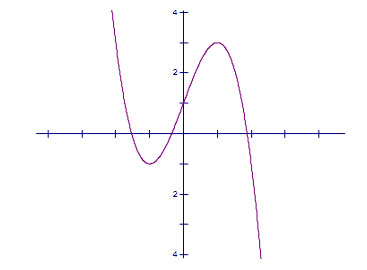
b. 1,0 điểm

y' = -3x² + 3m = -3(x² - m)

y' = 0 ↔ x² - m = 0

Đồ thị hàm số (1) có 2 điểm cực trị ↔ PT (*) có 2 nghiệm phân biệt ↔ m > 0 (**)

Khi đó 2 điểm cực trị A(-√m; 1 - 2m√m), B(√m; 1 + 2m√m)

Tam giác OAB vuông tại O ↔ 4m³ + m - 1 ↔ m = 1/2 (TM (**))

Vậy m = 1/2.

Câu 2 (1,0 điểm)

sin2x + 1 = 6sinx + cos2x

↔ (sin2x - 6sinx) + (1 - cos2x) = 0

↔ 2sinx(cosx - 3) + 2sin²x = 0

↔ 2sinx(cosx - 3 + sin x) = 0

↔ sin x = 0 hoặc sin x + cosx = 3 (VN)

↔ x = kπ. Vậy nghiệm của PT là x = kπ, k ϵ Z.