Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Lương Ngọc Quyến
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Lương Ngọc Quyến là đề thi thử đại học môn Toán có đáp án chi tiết, rõ ràng giúp các bạn ôn tập thật tốt, luyện thi đại học môn Toán hiệu quả, chuẩn bị cho kì thi THPT Quốc gia năm 2016 sắp tới.
Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Thủ Đức, Hồ Chí Minh
Đề thi thử THPT môn Toán lần 2 năm 2015 trường THPT Hai Bà Trưng, Thừa Thiên Huế
|
SỞ GD-ĐT THÁI NGUYÊN TRƯỜNG THPT LƯƠNG NGỌC QUYẾN |
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2015 Môn: Toán Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (2,0 điểm). Cho hàm số y = (-x + m)/(x + 2) (Cm).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
b) Tìm các giá trị thực của tham số m để đường thẳng d: 2x + 2y - 1 = 0 cắt đồ thị (Cm) tại hai điểm phân biệt A, B sao cho tam giác có diện tích bằng 1 (O là gốc toạ độ).
Câu 2 (1,0 điểm).
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = (x² + x + 1)/(x + 1) trên đoạn [1/2; 2].
b) Tính tích phân:
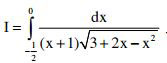
Câu 3 (2,0 điểm). Giải các phương trình sau:
a) log3(x - 1)² + log√3(2x -1) = 2.
b) (3sin2x - 2sinx)/(sin2x.cosx) = 2.
Câu 4 (1,0 điểm).
a) Cho số phức z thỏa mãn: (2 + i)z + (1 - i)/(1 + i) = 5 - i. Tính mô đun của số phức w = z + z².
b) Một lớp học có 20 học sinh nam và 15 học sinh nữ. Thầy giáo chủ nhiệm chọn ra 5 học sinh để thành lập một tốp ca hát chào mừng ngày thành lập Quân đội nhân dân Việt Nam (22 tháng 12). Tính xác suất sao cho trong đó có ít nhất một học sinh nữ.
Câu 5 (1,0 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên SAB là tam giác vuông cân tại đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SB và AC
Câu 6 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Điểm F(11/2; 3) là trung điểm của cạnh AD. Đường thẳng EK có phương trình 19x - 8y - 18 = 0 với E là trung điểm của cạnh AB, điểm K thuộc cạnh DC và KD = 3KC. Tìm tọa độ điểm C của hình vuông ABCD biết điểm E có hoành độ nhỏ hơn 3.
Câu 7 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): 2x - 2y - z - 4 = 0 và mặt cầu (S): x² + y² + z² - 2x - 4y - 6z - 11 = 0. Chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn. Xác định toạ độ tâm và tính bán kính của đường tròn đó.
Câu 8 (1,0 điểm). Cho a, b, c là ba số thực dương. Chứng minh rằng:
![]()
Đáp án đề thi thử THPT Quốc gia môn Toán
Lưu ý khi chấm bài:
- Đáp án chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài làm của học sinh. Khi chấm nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không được điểm.
- Học sinh được sử dụng kết quả phần trước để làm phần sau.
- Trong lời giải câu 5, nếu học sinh không vẽ hình hoặc vẽ sai hình thì không cho điểm.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
Câu 1:
a, y = (-x + 1)/(x + 2)
TXĐ: D = R\{-2}.
- Giới hạn:
| lim | y = -1 | lim | y = -1 |
| x→-∞ | x→+∞ |
+) Đường thẳng y = -1 là tiệm cân ngang của đồ thị hàm số.
| lim | y = +∞ | lim | y = -∞ |
| x→(-2)+ | x→(-2)- |
+) Đường thẳng x = -2 là tiệm cận đứng của đồ thị hàm số.
- Chiều biến thiên y' = -3/(x + 2)² < 0 với mọi x ≠ -2.
- Hàm số nghịch biến trên mỗi khoảng (-∞;-2) và (-2; +∞)
- Hàm số không có cực trị
- Bảng biến thiên
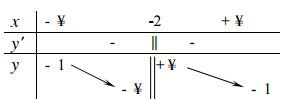
- Đồ thị;
- Giao với trục Ox tại A(1;0)
- Giao với trục Oy tại 1 B(0;1/2)
- Đồ thị nhận I(-2;-1) giao của hai tiệm cận làm tâm đối xứng
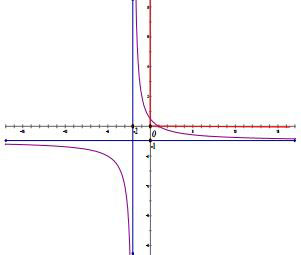
(Còn tiếp)