Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Sơn Tây, Hà Nội

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Sơn Tây, Hà Nội là đề thi thử đại học có đáp án, dành cho các bạn luyện thi đại học môn Toán tham khảo, luyện đề, ôn tập chuẩn bị tốt cho kì thi THPT Quốc gia môn Toán sắp tới, ôn thi đại học môn Toán được chắc chắn nhất.

Đề thi thử Quốc gia môn Toán

TRƯỜNG THPT SƠN TÂY

ĐỀ THI THỬ THPT QUỐC GIA 2015 LẦN 1 Môn: Toán (Thời gian làm bài 180 phút)

Câu 1 (2 điểm). Cho hàm số y = x⁴/2 - 3x² + 5/2.

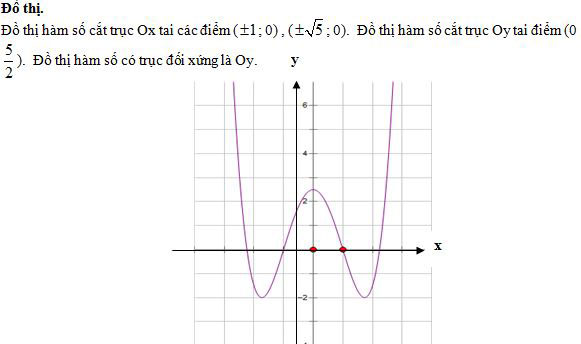
1. Khảo sát sự biến thiên và vẽ đồ thi (C) của hàm số.
2. Cho điểm M thuộc (C) có hoành độ x_M = a. Viết phương trình tiếp tuyến của (C) tại M, với giá trị nào của a thì tiếp tuyến của (C) tại M cắt (C) tại hai điểm phân biệt khác M.

Câu 2 (1 điểm). Giải phương trình: sinx + cosx = -2cos3x

Câu 3 (1 điểm). Giải phương trình: 1/2.log_√2(x + 3) + 1/4log₄(x + 1)⁸ = 3log₈(4x).

Câu 4(1 điểm). Tính tích phân:

p
∫	(1 + cosx)xdx
0

Câu 5 (1 điểm). Tìm m để phương trình sau đây có đúng 2 nghiệm thực phân biệt:

√(2 - x) - √(2 + x) - √((2 - x)(2 +x)) = m

Câu 6 (1 điểm). Cho hình chóp lục giác đều S.ABCDEF với SA = a, AB = b. Tính thể tích của hình chóp đó và khoảng cách giữa các đường thẳng SA, BE.

Câu 7(1 điểm) Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình 2x - y + 2z - 1 = 0 và điểm A(1, 3, -2).

1. Tìm tọa độ hình chiếu của A trên mặt phẳng (P).
2. Viết phương trình mặt cầu tâm A và đi qua gốc tọa độ O.

Câu 8(1 điểm) Trong mặt phẳng tọa độ Oxy cho tam giác ABC vuông cân tại A. Biết M(1; -1) là trung điểm của BC và G(2/3; 0) là trọng tâm tam giác ABC. Tìm tọa độ các đỉnh A, B, C.

Câu 9(1 điểm) Cho x, y, z là ba số thực dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức:

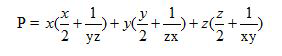
Đáp án đề thi thử THPT Quốc gia môn Toán

Câu 1:

1. Ta có hàm số y = x⁴/2 - 3x² + 5/2

- Tập xác định D = R.

- Sự biến thiên.

+) Chiều biến thiên:

y’ = 2x³ - 6x , y’ = 0 ↔ x = 0 v x = ± √3

• y’< 0 " với mọi x thuộc khoảng ( -∞; -√3) υ (0,√3). Hàm số nghịch biến trên khoảng ( -∞; -√3) và (0, √3).
• y’ > 0 " với mọi x thuộc khoảng (-√3; 0) υ (√3; +∞).Hàm số đồng biến trên các khoảng (-√3; 0) và (√3; +∞).

- Cực trị. Hàm số đạt cực đại tại x = 0, y_CĐ = y(0) = 5/2. Hàm số đạt cực tiểu tại x = ±√3, yCT = y(±√3) = - 2.

- Giới hạn:

lim	(x4/2 - 3x2 + 5/2) = + ∞	;	lim	(x4/2 - 3x2 + 5/2) = + ∞
x→ -∞			x→+∞

Suy ra đồ thị hàm số không có tiệm cận.

Tính lồi, lõm và điểm uốn.

y’’ = 6x² - 6 , y’’ = 0 → x = ±1. Đồ thị nhận các điểm I(±1; 0) là điểm uốn.

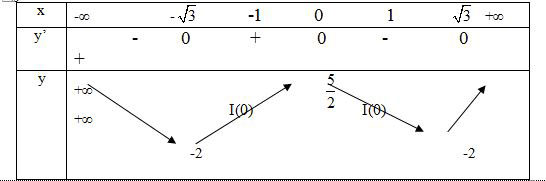
Bảng biến thiên.