Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Thủ Đức, Hồ Chí Minh
Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Thủ Đức, Hồ Chí Minh mà VnDoc gửi tới các bạn hy vọng sẽ là một trong những tài liệu ôn luyện thi đại học môn Toán hay, giúp các bạn tự kiểm tra trình độ bản thân, hệ thống kiến thức, chuẩn bị tốt nhất cho kì thi đại học cũng như kì thi tốt nghiệp môn Toán sắp tới.
Đề thi thử Quốc gia môn Toán
| SỞ GDĐT HỒ CHÍ MINH TRƯỜNG THPT THỦ ĐỨC GV: PHẠM THỊ THỦY |
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015 Môn: TOÁN |
Câu 1 (2.0 điểm). Cho hàm số:
| y = | 2x + 1 |
| x - 1 |
a) Khảo sát sự biến thiên và vẽ đồ thị ( C) của hàm số (1) .
b) Gọi M là giao điểm của (C) và 0x. Viết phương trình tiếp tuyến với (C) tại M.
Câu 2 (1 điểm).
a, Giải phương trình: cos2x + (1 + 2cosx)(sinx - cosx) = 0, x thuộc R.
b, Tìm tọa độ điểm biểu diễn số phức z biết:
| _ | ||
| iz + (2 - i) | z | = 3 - i |
Câu 3 (1.0 điểm).
a) Giải bất phương trình: log2(x² + 2x) + log1/2(3x + 2) ≥ 0, x thuộc R.
b) Giải bóng chuyền VTV cup gồm 9 đội bóng tham dự, trong đó có 6 đội nước ngoài và 3 đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng A,B,C mỗi bảng 3 đội. Tính xác suất để 3 đội bóng của VN ở ba bảng khác nhau.
Câu 4 (1 điểm) Tính tích phân
![]()
Câu 5 (1.0 điểm). Cho hình chóp đều SABC có SA = 2a, AB = a. M là trung điểm cạnh BC. Tính theo a thể tích khối SABC và khoảng cách giữa hai đường thẳng AM, SB.
Câu 6 (1.0 điểm). Trong không gian 0xyz cho mặt phẳng (P): 2x + 3y + z – 11 = 0. Viết phương trình mặt cầu (S) có tâm I(1; -2; 1) và tiếp xúc với (P). Tìm tọa độ tiếp điểm.
Câu 7 (1.0 điểm). Trong mp tọa độ 0xy, cho tam giác ABC nhọn có đỉnh A(-1;4) trực tâm H. Đường thẳng AH cắt cạnh BC tại M. Đường thẳng CH cắt cạnh AB tại N. Tâm đường tròn ngoại tiếp tam giác HMN là I(2; 0). Đường thẳng BC đi qua P(1; -2). Tìm tọa độ các đỉnh B,C của tam giác biết B thuộc đường thẳng d: x + 2y – 2 = 0.
Câu 8 (1.0 điểm). Giải hệ phương trình

Câu 9 (1 điểm): Cho x, y, z là các số thực dương thỏa mãn 5(x² + y² + z²) = 9(xy + 2yz + zx). Tìm giá trị lớn nhất của biểu thức:
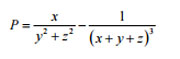
Đáp án đề thi thử Quốc gia môn Toán
Câu 1:
b, Giao điểm M(-0,5, 0). Phương trình tiếp tuyến tại M là y = -4x/3 - 2/3.
Câu 2:
a, cos2x + (1 + 2cosx)(sinx - cosx) = 0 ↔ (cosx - sinx)(sinx - cosx - 1) = 0
Đáp số: x = π/4 + kπ; x = π/2 + l2π; x = π + m2π.
b, Gọi z = a + bi, a, b thuộc R,
Ta có phương trình đề bài cho tương đương với (a + bi) + (2 - i)(a - bi) = 3i - 1 (1)
Giải phương trình (1) được a = -2, b = -3/2.
Câu 3:
a, Tập nghiệm S = [2, +∞).
b) Số phần tử của không gian mẫu là 1680, Số kết quả thuận lợi cho biến cố A là 540. Xác suất cần tìm P(A) = 9/28.
Câu 4: Tích phân I = 4/3 + e
Câu 5: VS.ABC = a³√11/12 ; d[AM, SB] = a√517/47
Câu 6:
Phương trình mặt cầu (x -1)² + (y + 2)² + (z - 1)² = 14.
Tọa độ tiếp điểm H(3;-1;2).


