Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Chuyên Đại học Vinh, Nghệ An
Đề thi thử Quốc gia môn Toán
Nhằm giúp các bạn thử sức trước kì thi THPT Quốc gia 2015, VnDoc xin giới thiệu đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Chuyên Đại học Vinh, Nghệ An có đáp án kèm theo. Hi vọng tài liệu này giúp các bạn ôn luyện môn Toán hiệu quả và đạt kết quả cao trong kì thi tới. Mời các bạn tham khảo.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Vinh (Lần 1)
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Đại học Vinh (Lần 2)
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2015 trường THPT Chuyên Đại học Vinh, Nghệ An
|
TRƯỜNG ĐẠI HỌC VINH TRƯỜNG THPT CHUYÊN |
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015 – LẦN 1 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (2,0 điểm). Cho hàm số
![]()
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 2.
b) Tìm m để hàm số (1) có cực đại là yCĐ thỏa mãn yCĐ = 1/3.
Câu 2 (1,0 điểm).
a) Giải phương trình cos3x + cosx = 2√3cos2xsinx.
b) Tìm phần thực và phần ảo của số phức z thỏa mãn
![]()
Câu 3 (0,5 điểm). Giải phương trình log4x² + log2(2x - 1) = log2(4x + 3).
Câu 4 (1,0 điểm). Giải bất phương trình x² + 5x < 4(1 + √(x³ + 2x² - 4x)).
Câu 5 (1,0 điểm). Tính tích phân
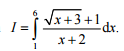 ²²
²²
Câu 6 (1,0 điểm). Cho hình chóp đều S.ABC có SA = 2a, AB = a. Gọi M là trung điểm cạnh BC. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng AM, SB.
Câu 7 (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có góc ACD = α với cosα = 1/√5, điểm H thỏa mãn điều kiện véc tơ HB = -2. véc tơ HC, K là giao điểm của hai đường thẳng AH và BD. Cho biết H(1/3, -4/3), K(1, 0) và điểm B có hoành độ dương. Tìm tọa độ các điểm A, B, C, D.
Câu 8 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y + z - 3 = 0 và đường thẳng d: (x - 2)/1 = (y + 1)/-2 = z/-1. Tìm tọa độ giao điểm của (P) và d; tìm tọa độ điểm A thuộc d sao cho khoảng cách từ A đến (P) bằng 2√3.
Câu 9 (0,5 điểm). Giải bóng chuyền VTV Cup gồm 9 đội bóng tham dự, trong đó có 6 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C; mỗi bảng có 3 đội. Tính xác suất để 3 đội bóng của Việt Nam ở ba bảng khác nhau.
Câu 10 (1,0 điểm). Giả sử x, y, z là các số thực không âm thỏa mãn:
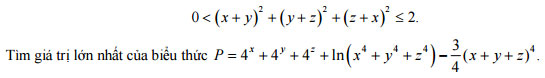
Đáp án đề thi thử Quốc gia môn Toán
Danh sách 65 cụm thi tỉnh kỳ thi THPT quốc gia
Những đồ dùng được phép mang vào phòng thi kỳ thi THPT Quốc gia 2015
Câu 1 (2 điểm): Khi m = 2 thì phương trình y = x³/3 - x²/2 - 2x + 1/3.
Tập xác định: D = R.
Sự biến thiên
- Xét chiều biến thiên, ta có y' = x² - x - 2, (x thuộc R), suy ra
- y' = 0 tương đương x = -1 hoặc x = 2.
- y' < 0 tương đương -1 < x < 2,
- y' > 0 tương đương x < -1 hoặc x > 2.
Suy ra hàm số đồng biến trên mỗi khoảng (-∞; -1) và (2;+∞); hàm số nghịch biến trên khoảng (-1; 2).
- Cực trị:
- Hàm số đạt cực trị tại x = -1, yCĐ = y(-1) = 1,5
- Hàm số đạt cực tiểu tại x = 2, yCT = y(2) = -3.
- Giới hạn tại vô cực
![]()
- Bảng biến thiên và đồ thị hàm số:
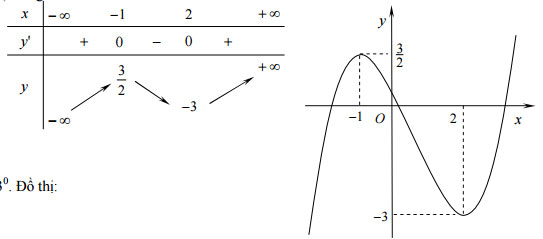
b) (1,0 điểm)
Ta có y' = x² - (m - 1)x - m với x thuộc R.
-) y' = 0 tương đương x = -1 hoặc x = m. suy ra hàm số có cực đại khi và chỉ khi m ≠ -1.
-) Với m < -1 thì hàm số đạt cực đại x = m, khi đó yCĐ = y(m) = -m³/6 - m²/2 + 1/3.
Ta có với yCĐ = 1/3 suy ra;
- m = - 3 (thỏa mãn).
- m = 0 (không thỏa mãn).
-) Với m > -1 thì hàm số đạt cực đại tại x = -1, với yCĐ = y(-1) = m/2 + 1/2.
Theo bài ra yCĐ = 1/3 ↔ m = -1/3 (thỏa mãn).
Vậy các giá trị cần tìm của m là m = -3; m = -1/3
Câu 2:
a) (0,5 điểm)
Phương trình đã cho tương đương với 2cos2xcosx = 2√3cos2xsinx
- cos2x = 0
- cosx = √3sinx
Với cos 2x = 0 suy ra x = π/4 + kπ/2. (k thuộc Z)
Với cosx = √3sinx suy ra x = π/6 + kπ.(k thuộc Z).
b) (0,5 điểm)
Đặt z = a + bi (a, b thuộc R). Từ giả thiết ta có a - bi + 2(a + bi) = 3 - 2i ↔ 3a + bi = 3 - 2i
- 3a = 3 → a = 1.
- b = -2 .
Vậy số phức z có phần thực bằng 1, phần ảo bằng -2.
(Còn tiếp)