Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Vinh (Lần 1)
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Vinh (Lần 1) được VnDoc.com sưu tầm và đăng tải, là tài liệu luyện tập hữu ích dành cho các bạn thí sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016, giúp các bạn nâng cao kỹ năng làm bài môn Toán.
TRƯỜNG ĐẠI HỌC VINH TRƯỜNG THPT CHUYÊN | ĐỀ THI THỬ THPT QUỐC GIA LẦN 1 MÔN TOÁN |
Câu 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x3 - 6x2 + 9x - 1.
Câu 2: Viết phương trình tiếp tuyến của đồ thị hàm số 
biết rằng tiếp tuyến song song với đường thẳng d: 3x + 4y - 2 = 0.
Câu 3:
a) Giải bất phương trình:
b) Cho log35 = a. Tính log√4575 theo a.
Câu 4: Tính tích phân:
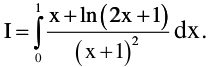
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y + z – 7 = 0 và đường thẳng
Tìm tọa độ giao điểm của d và (P) và lập phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với (P)
Câu 6:
a) Giải phương trình: cos x + sin 2x = sin x + sin 2x.cot x.
b) Nhân dịp kỉ niệm ngày Nhà giáo Việt Nam, trường THPT X tuyển chọn được 24 tiết mục văn nghệ tiêu biểu, trong số đõ lớp 11A có 2 tiết mục để công diễn toàn trường. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành hai buổi công diễn, mỗi buổi 12 tiết mục. Tính xác suất để 2 tiết mục của lớp 11A được biểu diễn trong cùng một buổi.
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SD vuông góc với mặt phẳng (ABCD), AD = a, AOB = 120o, góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 45o. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AC và SB.
Câu 8: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình các đường thẳng chứa đường trung tuyến và đường cao kẻ từ C lần lượt là: y + 2 = 0 và 3x - 2y + 8 = 0 . Đường thẳng chứa trung tuyến kẻ từ A đi qua K(-18;3) . Tính ABC biết rằng điểm A có tung độ âm và thuộc đường thẳng d: x + 2y + 2 = 0.
Câu 9: Giải bất phương trình:
Câu 10: Giả sử x, y, z là các số thực không âm thỏa mãn xy + yz + zx = 2. Tìm giá trị lớn nhất của biểu thức
