Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Đào Duy Từ, Thanh Hóa (Lần 3)

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Đào Duy Từ, Thanh Hóa (Lần 3) là đề thi thử đại học môn Toán có đáp án mà VnDoc.com xin gửi tới các bạn tham khảo và nghiên cứu, chuẩn bị ôn tập tốt nhất cho kì thi Quốc gia đang tới rất gần. Mời các bạn tham khảo.

Đề thi minh họa và đáp án kỳ thi THPT Quốc gia năm 2016 môn Toán

Đề thi thử đánh giá năng lực ĐHQGHN 2016: Tư duy định lượng (môn Toán)

SỞ GD & ĐT THANH HÓA TRƯỜNG THPT ĐÀO DUY TỪ

ĐỀ KHẢO SÁT CHẤT LƯỢNG THI THPT QUỐC GIA NĂM HỌC 2014 - 2015 Môn thi: TOÁN Thời gian làm bài: 180 phút, không kể thời gian giao đề Đề có 10 câu và 01 trang

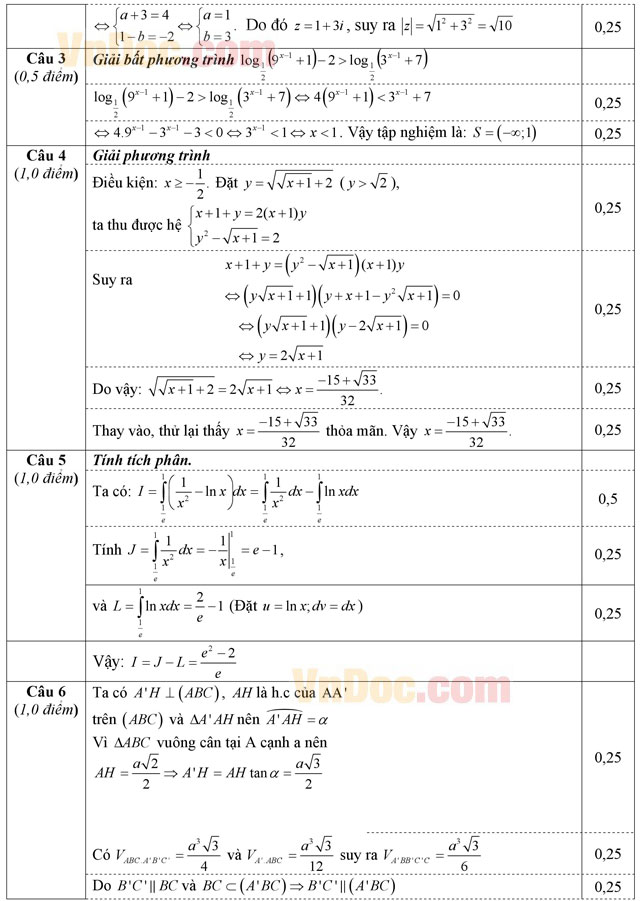
Câu 1 (2,0 điểm). Cho hàm số y = x³ + (m - 1)x² - m (1), với m là tham số

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 4.

b) Tìm các giá trị thực của m để hàm số (1) đạt cực đại tại x = -1. Khi đó hãy tìm tọa độ các điểm cực trị của đồ thị (C).

Câu 2 (1,0 điểm).

a) Giải phương trình tan2x - 2sin²x = sin2x.

b) Cho số phức z thỏa mãn hệ thức: . Tính môđun của z.

Câu 3 (0,5 điểm). Giải bất phương trình trên tập số thực:

Câu 4 (1,0 điểm). Giải phương trình trên tập số thực:

Câu 5 (1,0 điểm). Tính tích phân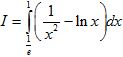

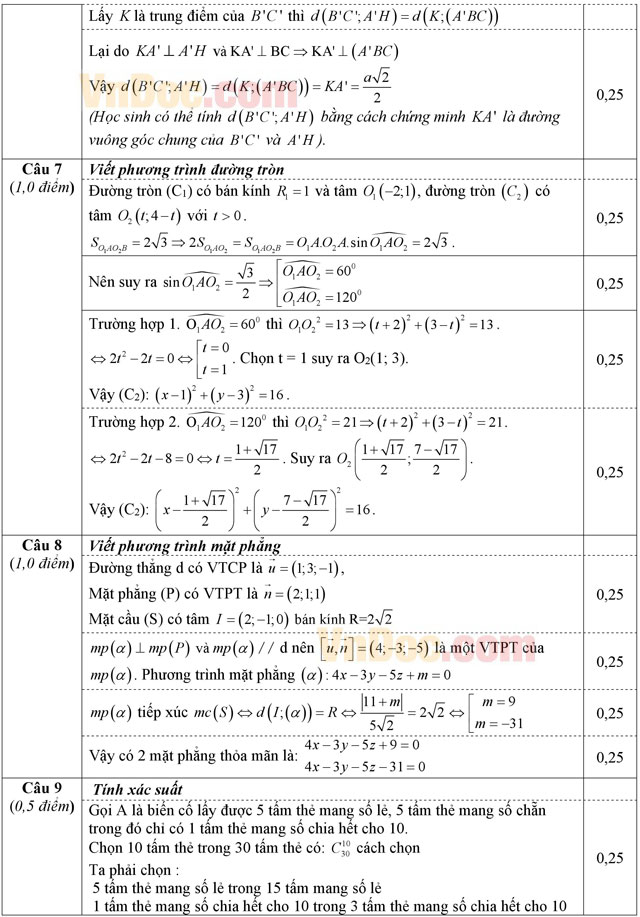
Câu 6 (1,0 điểm). Cho hình lăng trụ có đáylà tam giác vuông cân với AB = AC = a (a > 0). Hình chiếu vuông góc của A’ trên (ABC) là trung điểm H của BC, các cạnh bên của lăng trụ tạo với đáy một góc α có tanα = √6/2. Tính thể tích khối đa diện và khoảng cách giữa B’C và A’H.

Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy cho đường tròn (C₁): (x + 2)² + (y - 1)² = 1 có tâm O₁, đường tròn (C₂) bán kính bằng 4 có tâm O₂ nằm trên đường thẳng (d): x + y - 4 = 0 và cắt (C₁) tại hai điểm A và B sao cho tứ giác O₁AO₂B có diện tích bằng 2√3. Viết phương trình đường tròn (C₂) biết O₂ có hoành độ dương.

Câu 8 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, Viết phương trình mặt phẳng (α) song song với đường thẳng , vuông góc với mặt phẳng (P): 2x + y + z - 1 = 0 đồng thời tiếp xúc với mặt cầu (S): ( x - 2)² + (y + 1)² + z² = 8.

Câu 9 (0,5 điểm). Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có 1 tấm mang số chia hết cho 10.

Câu 10 (1,0 điểm). Cho các số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia môn Toán