Đề thi thử THPT Quốc gia môn Toán trường THPT Lương Ngọc Quyến, Thái Nguyên năm 2015 (Lần 2)

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia môn Toán trường THPT Lương Ngọc Quyến, Thái Nguyên năm 2015 (Lần 2) gồm 9 câu hỏi có đáp án đi kèm, là tài liệu ôn tập môn Toán, chuẩn bị cho kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016 sắp tới. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lương Ngọc Quyến, Thái Nguyên

Đề thi thử THPT Quốc gia môn Toán trường THPT Phú Nhuận, TP. HCM

Bộ công thức Toán lớp 12 ôn thi THPT Quốc gia từ A - Z

SỞ GD & ĐT THÁI NGUYÊN TRƯỜNG THPT LƯƠNG NGỌC QUYẾN

ĐỀ THI THỬ THPT QUỐC GIA LẦN 2 NĂM 2015 MÔN TOÁN Thời gian làm bài: 180 phút (không kể thời gian phát đề)

Câu 1 (2,0 điểm). Cho hàm số y = (1/4)x⁴ - 2x² - 1.

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Dựa vào đồ thị (C), biện luận theo m số nghiệm thực của phương trình -x⁴ + 8x² + 4m + 4 = 0.

Câu 2 (1,0 điểm). Giải các phương trình sau:

a) 7^√x + 2.7^{1 - √x} - 9 = 0

b) (sinx + cosx)2 = 1 + cosx.

Câu 3 (1,0 điểm).

a) Tìm phần thực và phần ảo của số phức:

b) Tìm hệ số của x9 trong khai triển (2 - 3x)²ⁿ, trong đó n là số nguyên dương thỏa mãn:

C¹_{2n + 1} + C³_{2n + 1} + C⁵_{2n + 1} + ... + C^{2n + 1}_{2n + 1} = 4096.

Câu 4 (1,0 điểm). Tính tích phân:

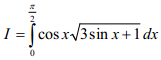
Câu 5 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt phẳng (SAB) vuông góc với đáy, tam giác SAB cân tại S và SC tạo với đáy một góc 60^o. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng BD và SA theo a.

Câu 6 (1,0 điểm). Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC nội tiếp đường tròn (T) có phương trình (x - 1)² + (y - 2)² = 25. Các điểm K(-1;1), H(2;5) lần lượt là chân đường cao hạ từ A, B của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC biết rằng đỉnh C có hoành độ dương.

Câu 7 (1,0 điểm).

Câu 8 (1,0 điểm). Giải hệ phương trình:

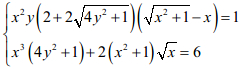
Câu 9 (1,0 điểm).

Cho 3 số thực dương x, y, z thay đổi, thỏa mãn x + y + 1 = z. Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán

Câu 1. a:

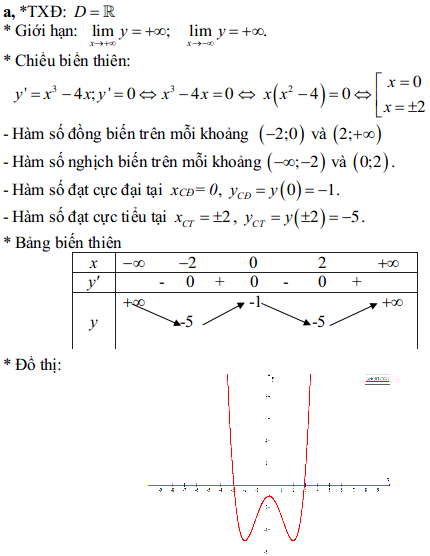
Câu 1.b:

Ta có: -x⁴ + 8x² + 4m + 4 = 0

(1/4)x⁴ - 2x² - 1 = m (*)

Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị (C) và đường thẳng d: y = m

• Nếu m > -1 hoặc m = - 5 thì d cắt (C) tại 2 điểm nên phương trình (*) có 2 nghiệm.
• Nếu m = - 1 thì d cắt (C) tại 3 điểm nên phương trình (*) có 3 nghiệm.
• Nếu thì d cắt (C) tại 4 điểm phân biệt nên phương trình (*) có 4 nghiệm phân biệt.
• Nếu m < -5 thì d không cắt (C) nên phương trình (*) vô nghiệm.

(Còn tiếp)