Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Chuyên Nguyễn Bỉnh Khiêm, Quảng Nam

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Chuyên Nguyễn Bỉnh Khiêm, Quảng Nam gồm 10 câu hỏi có đáp án đi kèm, đây là đề thi thử đại học môn Toán có cấu trúc tương đương đề thi THPT Quốc gia môn Toán chính thức của Bộ GD&ĐT. Tài liệu này giúp các bạn ôn thi THPT Quốc gia, luyện thi đại học môn Toán hiệu quả hơn. Mời các bạn cùng tham khảo.

Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Thanh Chương 3, Nghệ An

Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Nguyễn Hiền, Đà Nẵng

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

SỞ GD&ĐT QUẢNG NAM TRƯỜNG THPT CHUYÊN NGUYỄN BỈNH KHIÊM

KÌ THI THỬ THPT QUỐC GIA NĂM 2015 MÔN TOÁN Thời gian làm bài: 180 phút

Câu 1 (2,0 điểm) Cho hàm số y = x³ + 3x² - 2 (1)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số

b) Viết phương trình tiếp tuyến với đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng y = -1/9 x

Câu 2 (1,0 điểm)

a) Giải phương trình: cosx + 2cos² x/3 - 3 = 0

Câu 3 (0,5 điểm) Giải phương trình: log₄(x² - 7x + 10) - log₄(x - 2) = log_1/4(x + 5)

Câu 4 (1,0 điểm) Giải hệ phương trình

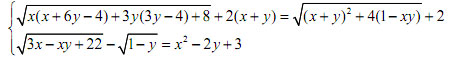
Câu 5 (1,0 điểm) Tính tích phân

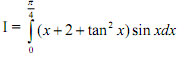
Câu 6 (1,0 điểm) Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a√3, BC = 3a, ACB =30⁰. Cạnh bên hợp với mặt phẳng đáy góc 60⁰ và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Tính thể tích khối lăng trụ ABC.A’B’C' và khoảng cách từ B đến mặt phẳng (A’AC).

Câu 7 (1,0 điểm) Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A(-3; -4), tâm đường tròn nội tiếp I(2; 1) và tâm đường tròn ngoại tiếp J(-1/2;1). Viết phương trình đường thẳng BC.

Câu 8 (1,0 điểm) Trong không gian tọa độ Oxyz, cho hai điểm A(4; -2; 11), B( -2; -10; 3) và mặt phẳng (P): x + y – z – 4 = 0. Viết phương trình mặt phẳng trung trực đoạn AB và tìm điểm M trên mặt phẳng (P) sao cho MA = MB = 13.

Câu 9 (0,5 điểm) Một hộp đựng 3 xanh, 4 bi đỏ và 5 bi vàng. Lấy ngẫu nhiên 5 bi từ hộp. Tính xác suất để trong 5 bi lấy ra có đủ 3 màu và số bi xanh và số bi đỏ bằng nhau.

Câu 10 (1,0 điểm) Cho hai số thực a, b thuộc khoảng (0, 1) thỏa mãn (a³ + b³)(a + b) -ab(a - 1)(b -1) = 0. Tìm giá trị lớn nhất của biểu thức sau:

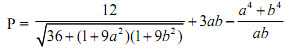
Đáp án đề thi thử THPT Quốc gia môn Toán

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 3

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 4

Câu 1 (2,0 điểm)

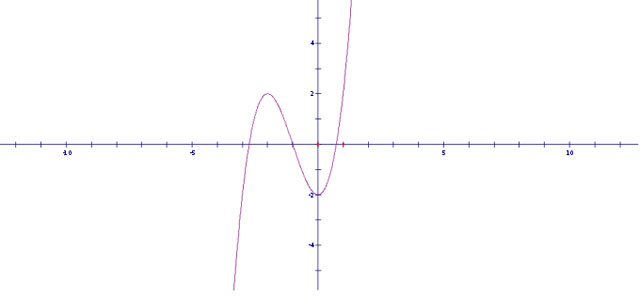
a. y = x³ + 3x² - 2

+ TXĐ: D = R

lim y	= -∞	lim y	= +∞
x→-∞		x→+∞

+ y' = 3x² + 6x, y' = 0 ↔ x = 0 → y = -2 hoặc x = -2 → y = 2

+ BBT

+ Hàm ĐB trên các khoảng (-∞; -2), (0; +∞) và NB trên khoảng (-2; 0). Điểm cực đại đồ thị (-2; 2); điểm cực tiểu đồ thị (0; -2)

+ Đồ thị

b) Tiếp tuyến vuông góc với đường thẳng y = -1/9 x nên tiếp tuyến có hệ số góc bằng 9.

Ta có y'(x₀) = 0 ↔ 3x₀² + 6x₀ = 9 ↔ x₀ = 1 → y₀ = 2 hoặc x₀ = -3 → y₀ = -2

• Phương trình tiếp tuyến tại điểm (1, 2) là y = 9(x - 1) + 2
• Phương trình tiếp tuyến tại điểm (-3, -2) là y = 9(x + 3) - 2

Câu 2 (1,0 điểm)

a. cosx + 2cos² x/3 - 3 = 0 ↔ 4cos3 x/3 - 3cos x/3 + 2 cos2 x/3 - 3 = 0

↔ (cos x/3 - 1) (4cos2 x/3 + 6cos x/3 + 3) = 0

↔ cos x/3 = 1 ↔ x/3 = k2π ↔ x =6kπ, k ϵ Z

(Còn tiếp)