Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 4

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 4 là bộ đề thi thử đại học môn Toán được VnDoc.com sưu tầm và tổng hợp. Đây sẽ là tài liệu hữu ích dành cho các bạn học sinh lớp 12, các bạn thí sinh tự do luyện đề, ôn thi đại học, ôn thi THPT Quốc gia môn Toán hiệu quả. Mòi các bạn cùng tham khảo.

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 3

Đề thi thử THPT Quốc gia năm 2016 môn Toán tỉnh Vĩnh Phúc (Lần 1)

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số .

Câu 2 (1,0 điểm). Tìm các điểm cực trị của đồ thị hàm số y = x³ - 3x² + 6.

Câu 3 (1,0 điểm).

a) Giải bất phương trình

b) Giải phương trình 5.9^x - 2.6^x = 3.4^x.

Câu 4 (1,0 điểm). Tính nguyên hàm

Câu 5 (1,0 điểm). Cho hình chóp S.ABC có SA⊥(ABC), góc ABC = 90⁰, AB = a, BC = a√3, SA = 2a. Chứng minh trung điểm I của cạnh SC là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD và tính diện tích mặt cầu đó theo a.

Câu 6 (1,0 điểm).

a) Giải phương trình: 2cos²x - sinx + 1 = 0.

b) Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng năm học. Tính xác suất sao cho lớp nào cũng có học sinh được chọn và có ít nhất 2 học sinh lớp 12A.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = 3a/2. Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của đoạn AD. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng HK và SD.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ toạ độ Oxy cho hình thang ABCD vuông tại A và D có AB = AD < CD, điểm B(1; 2), đường thẳng BD có phương trình là y - 2 = 0. Đường thẳng qua B vuông góc với BC cắt cạnh AD tại M. Đường phân giác trong góc MBC cắt cạnh DC tại N. Biết rằng đường thẳng MN có phương trình 7x - y - 25 = 0. Tìm tọa độ đỉnh D.

Câu 9 (1,0 điểm). Giải hệ phương trình: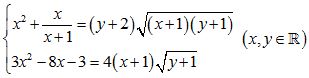

Câu 10 (1,0 điểm). Cho x, y ∈ R thỏa mãn 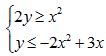. Tìm giá trị nhỏ nhất của biểu thức:

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Phù Cừ, Hưng Yên (Lần 1)

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số y = -x³ + 3x.

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [2; 4].

Câu 3 (1,0 điểm).

a) Giải phương trình: log₃(x² - x) + log_1/3(x + 4) = 1.

b) Giải bất phương trình: .

Câu 4 (1,0 điểm). Tính tích phân .

Câu 5 (1,0 điểm). Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P): x - y - 2z - 1 = 0 và hai điểm A(2; 0; 0), B(3; -1; 2). Viết phương trình mặt cầu (S) tâm I thuộc mặt phẳng (P) và đi qua các điểm A, B và điểm gốc toạ độ O.

Câu 6 (1,0 điểm).

a) Cho góc lượng giác α, biết tanα = 2. Tính giá trị biểu thức .

b) Trong kì thi học sinh giỏi cấp tỉnh của trường THPT Phù Cừ có 10 học sinh đạt giải trong đó có 4 học sinh nam và 6 học sinh nữ. Nhà trường muốn chọn một nhóm 5 học sinh trong 10 học sinh trên để tham dự buổi lễ tuyên dương khen thưởng cuối học kỳ 1 năm học 2015 – 2016 do huyện uỷ Phù Cừ tổ chức. Tính xác suất để chọn được một nhóm gồm 5 học sinh mà có cả nam và nữ, biết số học sinh nam ít hơn số học sinh nữ.

Câu 7 (1,0 điểm). Cho lăng trụ đứng ABCD.A'B'C'D', đáy là hình chữ nhật có AB = a, AD = a√3. Biết góc giữa đường thẳng A'C và mặt phẳng (ABCD) bằng 60⁰. Tính thể tích khối lăng trụ ABCD.A'B'C'D' và khoảng cách giữa hai đường thẳng chéo nhau B'C và C'D theo a.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ trục toạ độ Oxy, cho tam giác ABC vuông cân tại A. Gọi G là trọng tâm tam giác ABC. Điểm D thuộc tia đối của tia AC sao cho GD = GC. Biết điểm G thuộc đường thẳng d: 2x + 3y - 13 = 0 và tam giác BDG nội tiếp đường tròn (C): x² + y² - 2x - 12y + 27 = 0. Tìm toạ độ điểm B và viết phương trình đường thẳng BC, biết điểm B có hoành độ âm và toạ độ điểm G là số nguyên.

Câu 9 (1,0 điểm). Giải bất phương trình sau trên tập R:

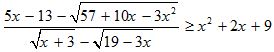
Câu 10 (1,0 điểm). Cho các số thực dương a, b, c. Chứng minh rằng:

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đồng Đậu, Vĩnh Phúc (Lần 2)

Câu 1 (2,0 điểm). Cho hàm số y = x³ - 3mx² + (m² - 1)x + 2, m là tham số.

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m = 1.
2. Tìm tất cả các giá trị của m để hàm số đã cho đạt cực tiểu tại x = 2.

Câu 2 (1,0 điểm).

1. Giải phương trình: log₂(x - 5) + log₂(x + 2) = 3
2. Giải phương trình: 7^x + 2.7^1-x - 9 = 0.

Câu 3 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x² - ln(1 - 2x) trên đoạn [-2; 0].

Câu 4 (1,0 điểm). Tìm hệ số của số hạng chứa x¹⁰ trong khai triển biểu thức , biết n là số tự nhiên thỏa mãn .

Câu 5 (1,0 điểm).

1. Cho góc α thỏa mãn π/2 < α < π và sin(α + π) = -1/3. Tính tan(7π/2 - α).
2. Trong cuộc thi "Rung chuông vàng" có 20 bạn lọt vào vòng chung kết, trong đó có 5 bạn nữ và 15 bạn nam. Để sắp xếp vị trí chơi, ban tổ chức chia các bạn thành 4 nhóm A, B, C, D, mỗi nhóm có 5 bạn. Việc chia nhóm được thực hiên bằng cách bốc thăm ngẫu nhiên. Tính xác suất để 5 bạn nữ thuộc cùng một nhóm.

Câu 6 (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mp(ABCD). Biết AC = 2a, BD = 4a. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AD và SC.

Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ với hệ trục tọa độ Oxy, cho hai đường thẳng có phương trình lần lượt là d₁: x - 2y + 2 = 0, d₂: 3x - 3y + √6 = 0 và tam giác ABC đều có diện tích bằng và trực tâm I thuộc d₁. Đường thẳng d₂ tiếp xúc với đường tròn nội tiếp tam giác ABC. Tìm tọa độ giao điểm d₁ và đường tròn ngoại tiếp tam giác ABC biết điểm I có hoành độ dương.

Câu 8 (1,0 điểm). Giải hệ phương trình: .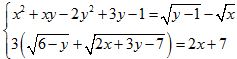

Câu 9 (1,0 điểm). Cho các số thực dương a, b thỏa mãn a² + 2b = 12. Tìm giá trị nhỏ nhất của biểu thức:

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Việt Trì, Phú Thọ (Lần 1)

Câu 1 (2.0 điểm). Cho hàm số y = x³ - 6x² + 9x - 2 (1).

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).

b) Viết phương trình đường thẳng đi qua điểm A(-1; 1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C).

Câu 2 (1.0 điểm).

Tìm giá trị lớn nhất và nhỏ nhất của hàm số: y = x⁴ - 2x² + 3 trên đoạn [0; 4].

Câu 3 (1.0 điểm).

a) Cho sinα = 1/2. Tính giá trị biểu thức .

b) Giải phương trình:

Câu 4 (1.0 điểm).

a)Tìm hệ số của số hạng chứa x⁵ trong khai triển: .

b) Trong bộ môn Toán, thầy giáo có 40 câu hỏi khác nhau gồm 5 câu hỏi khó, 15 câu hỏi trung bình, 20 câu hỏi dễ. Một ngân hàng đề thi mỗi đề thi có 7 câu hỏi đựơc chọn từ 40 câu hỏi đó. Tính xác suất để chọn được đề thi từ ngân hàng đề nói trên nhất thiết phải có đủ 3 loại câu hỏi (khó, trung bình, dễ) và số câu hỏi dễ không ít hơn 4.

Câu 5 (1.0 điểm).

Giải bất phương trình:

Câu 6 (1.0 điểm).

Cho lăng trụ đứng ABC.A'B'C', có đáy là tam giác vuông tại A, AB = a, AC = a√3, mặt bên BCC'B' là hình vuông, M, N lần lượt là trung điểm của CC' và B'C'. Tính thể tích khối lăng trụ ABC.A'B'C' và tính khoảng cách giữa hai đường thẳng A'B' và MN.

Câu 7 (1.0 điểm).

Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác nội tiếp trong đường tròn (C): x² + y² - 3x - 5y + 6 = 0. Trực tâm của tam giác ABC là H(2; 2) và đoạn BC = √5. Tìm tọa độ các điểm A, B, C biết điểm A có hoành độ dương.

Câu 8 (1.0 điểm).

Giải hệ phương trình: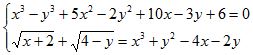

Câu 9 (1.0 điểm).

Cho ba số thực dương và thỏa mãn điều kiện a² + b² + c² = 3. Tìm giá trị nhỏ nhất của biểu thức:

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Phan Thúc Trực, Nghệ An (Lần 1)

Câu 1: (2,0 đ) Cho hàm số y = -x³ + 3x - 2 (1)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).

b) Viết phương trình tiếp tuyến của đồ thi (C) tại các giao điểm của (C) với đường thẳng d: y = -x - 2 biết tọa độ tiếp điểm có hoành độ dương.

Câu 2: (0,5đ) Giải phương trình:

Câu 3: (0,5đ) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = -2x⁴ + 4x² + 10 trên đoạn [0;2]

Câu 4: (1,0đ) Tính tích phân:

Câu 5: (1,0đ) Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;1;-3), B(4;3;-2), C(6;-4;-1). Chứng minh rằng A, B,C là ba đỉnh của một tam giác vuông và viết phương trình mặt cầu tâm A đi qua trọng tâm G của tam giác ABC.

Câu 6: (1,0đ)

a) Cho góc thỏa mãn: π < α < 3π/2 và tan = 2. Tính giá trị của biểu thức A = sin2α + cos(α + π/2)

b) Trong cụm thi để xét công nhận tốt nghiệp THPT thí sinh phải thi 4 môn trong đó có 3 môn bắt buộc là Toán, Văn, Ngoại ngữ và một môn do thí sinh tự chọn trong số các môn: Vật lí, Hóa học, Sinh học, Lịch sử và Địa lí. Trường A có 30 học sinh đăng kí dự thi, trong đó có 10 học sinh chọn môn Lịch sử. Lấy ngẫu nhiên 5 học sinh bất kỳ của trường A, tính xác suất để trong 5 học sinh đó có nhiều nhất 2 học sinh chọn môn Lịch sử.

Câu 7: (1,0đ) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 3a, hình chiếu của S lên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho AB = 3AH. Góc tạo bởi SA và mặt phẳng (ABC) bằng. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SA và BC.

Câu 8: (1,0đ) Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD với AB//CD có diện tích bằng 14, H(-1/2;0) là trung điểm của cạnh BC và I (1/4;1/2) là trung điểm của AH. Viết phương trình đường thẳng AB biết đỉnh D có hoành độ dương và D thuộc đường thẳng d: 5x - y + 1 = 0.

Câu 9: (1,0đ) Giải hệ phương trình:

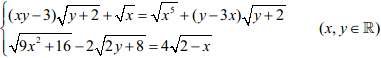
Câu 10: (1,0đ) Cho x, y là hai số thực dương thỏa mãn 2x + 3y ≤ y. Tìm giá trị nhỏ nhất của biểu thức