Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Phù Cừ, Hưng Yên (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Phù Cừ, Hưng Yên (Lần 1) có đáp án đi kèm, là tài liệu ôn tập môn Toán hữu ích dành cho các bạn học sinh lớp 12, các bạn thí sinh tự do, giúp các bạn luyện thi Đại học môn Toán hiệu quả, chuẩn bị sẵn sàng bước vào kì thi THPT Quốc gia 2016. Mời các bạn tham khảo.

Bộ đề thi thử THPT Quốc gia năm 2016 môn Vật Lý - Số 4

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

TRƯỜNG THPT PHÙ CỪ TỔ TOÁN - TIN ĐỀ CHÍNH THỨC

ĐỀ THI THỬ KỲ THI THPT QUỐC GIA NĂM 2016 MÔN: TOÁN – Ngày thi: 31/01/2016 – Lần 1 Thời gian làm bài: 180 phút không kể giao đề

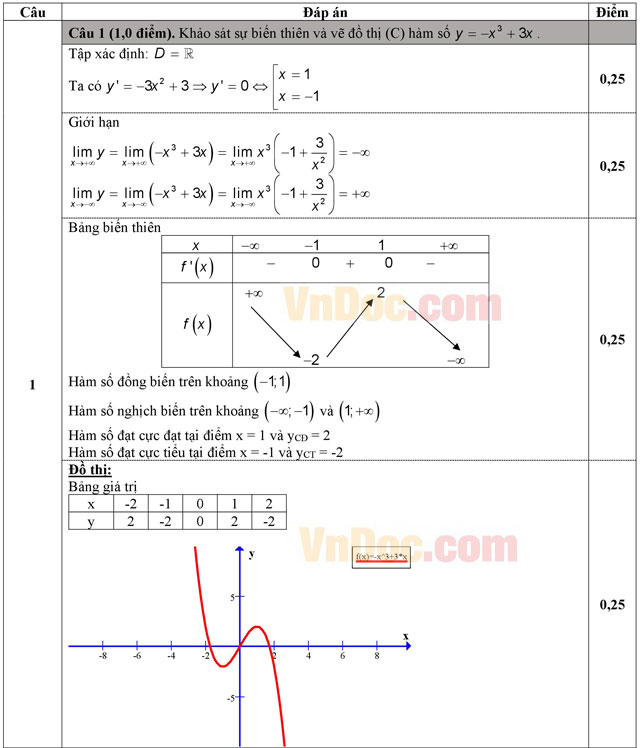
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số y = -x³ + 3x.

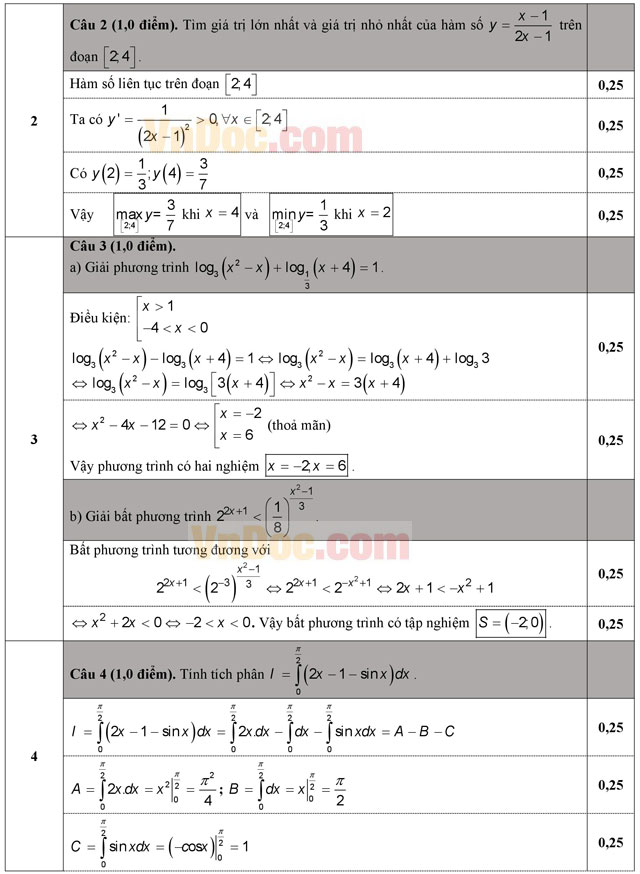
Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [2; 4].

Câu 3 (1,0 điểm).

a) Giải phương trình: log₃(x² - x) + log_1/3(x + 4) = 1.

b) Giải bất phương trình: .

Câu 4 (1,0 điểm). Tính tích phân .

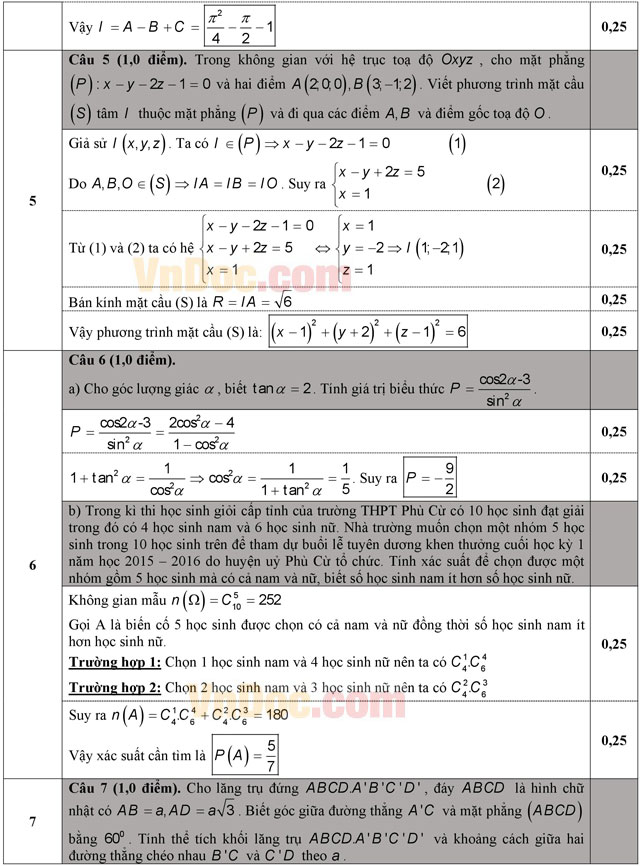
Câu 5 (1,0 điểm). Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P): x - y - 2z - 1 = 0 và hai điểm A(2; 0; 0), B(3; -1; 2). Viết phương trình mặt cầu (S) tâm I thuộc mặt phẳng (P) và đi qua các điểm A, B và điểm gốc toạ độ O.

Câu 6 (1,0 điểm).

a) Cho góc lượng giác α, biết tanα = 2. Tính giá trị biểu thức .

b) Trong kì thi học sinh giỏi cấp tỉnh của trường THPT Phù Cừ có 10 học sinh đạt giải trong đó có 4 học sinh nam và 6 học sinh nữ. Nhà trường muốn chọn một nhóm 5 học sinh trong 10 học sinh trên để tham dự buổi lễ tuyên dương khen thưởng cuối học kỳ 1 năm học 2015 – 2016 do huyện uỷ Phù Cừ tổ chức. Tính xác suất để chọn được một nhóm gồm 5 học sinh mà có cả nam và nữ, biết số học sinh nam ít hơn số học sinh nữ.

Câu 7 (1,0 điểm). Cho lăng trụ đứng ABCD.A'B'C'D', đáy là hình chữ nhật có AB = a, AD = a√3. Biết góc giữa đường thẳng A'C và mặt phẳng (ABCD) bằng 60⁰. Tính thể tích khối lăng trụ ABCD.A'B'C'D' và khoảng cách giữa hai đường thẳng chéo nhau B'C và C'D theo a.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ trục toạ độ Oxy, cho tam giác ABC vuông cân tại A. Gọi G là trọng tâm tam giác ABC. Điểm D thuộc tia đối của tia AC sao cho GD = GC. Biết điểm G thuộc đường thẳng d: 2x + 3y - 13 = 0 và tam giác BDG nội tiếp đường tròn (C): x² + y² - 2x - 12y + 27 = 0. Tìm toạ độ điểm B và viết phương trình đường thẳng BC, biết điểm B có hoành độ âm và toạ độ điểm G là số nguyên.

Câu 9 (1,0 điểm). Giải bất phương trình sau trên tập R:

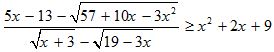
Câu 10 (1,0 điểm). Cho các số thực dương a, b, c. Chứng minh rằng:

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán