Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Việt Trì, Phú Thọ (Lần 1)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Việt Trì, Phú Thọ (Lần 1) là đề thi thử đại học môn Toán có đáp án dành cho các bạn học sinh và thầy cô tham khảo, luyện thi đại học môn Toán, làm quen nhiều dạng đề chuẩn bị sẵn sàng bước vào kì thi THPT Quốc gia môn Toán, ôn thi tốt nghiệp môn Toán.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đồng Đậu, Vĩnh Phúc (Lần 2)
|
TRƯỜNG THPT VIỆT TRÌ
|
ĐỀ THI THỬ THPT QUỐC GIA 2015-2016- LẦN 1 Môn: Toán Thời gian làm bài 180 phút, không kể thời gian giao đề |
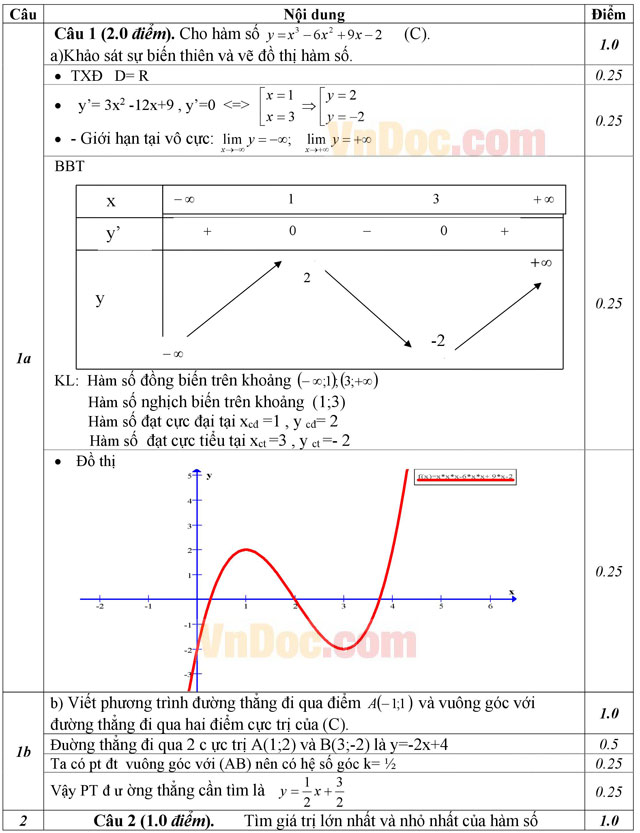
Câu 1 (2.0 điểm). Cho hàm số y = x3 - 6x2 + 9x - 2 (1).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
b) Viết phương trình đường thẳng đi qua điểm A(-1; 1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C).
Câu 2 (1.0 điểm).
Tìm giá trị lớn nhất và nhỏ nhất của hàm số: y = x4 - 2x2 + 3 trên đoạn [0; 4].
Câu 3 (1.0 điểm).
a) Cho sinα = 1/2. Tính giá trị biểu thức ![]() .
.
b) Giải phương trình: ![]()
Câu 4 (1.0 điểm).
a)Tìm hệ số của số hạng chứa x5 trong khai triển: ![]() .
.
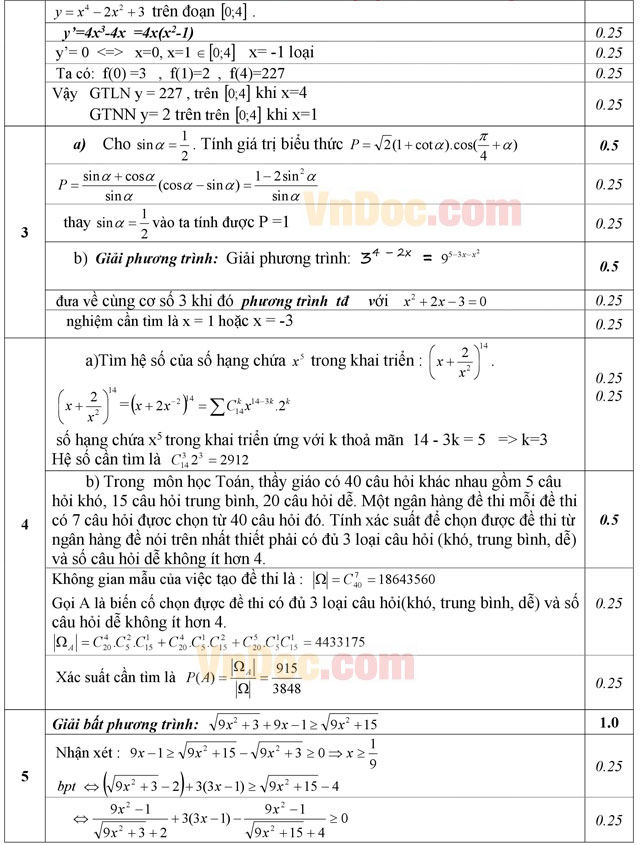
b) Trong bộ môn Toán, thầy giáo có 40 câu hỏi khác nhau gồm 5 câu hỏi khó, 15 câu hỏi trung bình, 20 câu hỏi dễ. Một ngân hàng đề thi mỗi đề thi có 7 câu hỏi đựơc chọn từ 40 câu hỏi đó. Tính xác suất để chọn được đề thi từ ngân hàng đề nói trên nhất thiết phải có đủ 3 loại câu hỏi (khó, trung bình, dễ) và số câu hỏi dễ không ít hơn 4.
Câu 5 (1.0 điểm).
Giải bất phương trình: ![]()
Câu 6 (1.0 điểm).
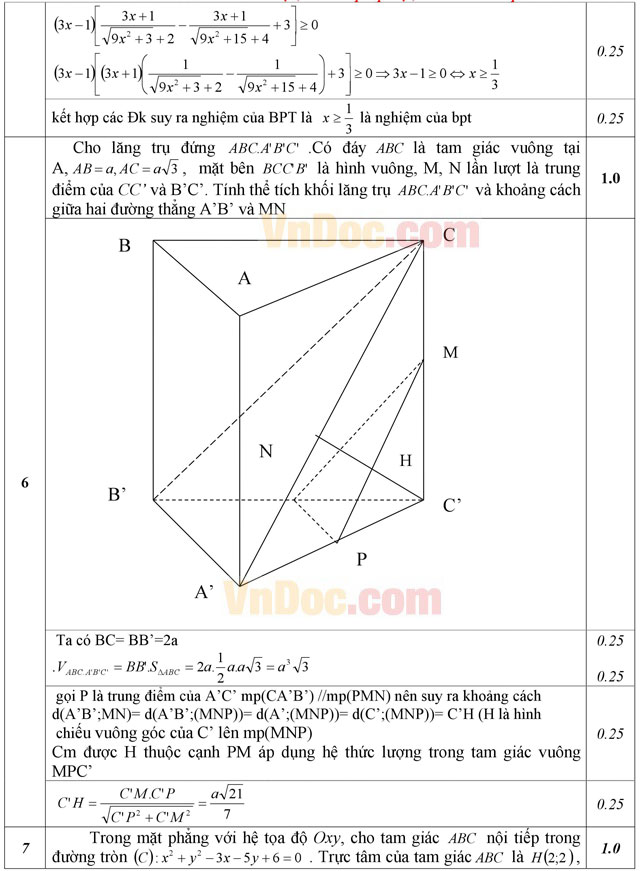
Cho lăng trụ đứng ABC.A'B'C', có đáy là tam giác vuông tại A, AB = a, AC = a√3, mặt bên BCC'B' là hình vuông, M, N lần lượt là trung điểm của CC' và B'C'. Tính thể tích khối lăng trụ ABC.A'B'C' và tính khoảng cách giữa hai đường thẳng A'B' và MN.
Câu 7 (1.0 điểm).
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác nội tiếp trong đường tròn (C): x2 + y2 - 3x - 5y + 6 = 0. Trực tâm của tam giác ABC là H(2; 2) và đoạn BC = √5. Tìm tọa độ các điểm A, B, C biết điểm A có hoành độ dương.
Câu 8 (1.0 điểm).
Giải hệ phương trình: 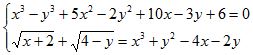
Câu 9 (1.0 điểm).
Cho ba số thực dương và thỏa mãn điều kiện a2 + b2 + c2 = 3. Tìm giá trị nhỏ nhất của biểu thức: ![]()
Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán