Đề thi thử Quốc gia lần 2 năm 2015 môn Toán trường THPT Tĩnh Gia 1, Thanh Hóa
Đề thi thử Quốc gia lần 2 năm 2015 môn Toán trường THPT Tĩnh Gia 1, Thanh Hóa là đề thi thử môn Toán có chất lượng, bao gồm đề thi và đáp án thi thử quốc gia 2015 của trường Tĩnh Gia 1 môn Toán. Hi vọng bộ tài liệu này giúp các bạn ôn thi THPT Quốc gia, ôn thi đại học có hiệu quả.
Đề thi thử Quốc gia lần 2 năm 2015 môn Hóa học trường THPT Tĩnh Gia 1, Thanh Hóa
Đề thi thử Quốc gia lần 2 năm 2015 môn Vật Lý trường THPT Tĩnh Gia 1, Thanh Hóa
Đề thi thử Quốc gia lần 2 năm 2015 môn Sinh học trường THPT Tĩnh Gia 1, Thanh Hóa
Đề thi thử THPT Quốc gia môn Toán
| SỞ GD & ĐT THANH HOÁ TRƯỜNG THPT TĨNH GIA 1 |
ĐỀ KIỂM TRA CHẤT LƯỢNG THPT QUỐC GIA LẦN 2 MÔN TOÁN (Năm học 2014 – 2015) Thời gian: 180 phút (không kể thời gian phát đề) |
Câu 1: ( 2 điểm) Cho hàm số y = x3 – 3mx2 + m (1)
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = 1
b) Tìm m để đồ thị hàm số đạt cực trị tại A, B sao cho diện tích tam giác OAB bằng 4 (O là gốc tọa độ)
Câu 2: (2 điểm)
a) Giải phương trình: sin 2x - cos2x = 2sin - 1
b) Tính tích phân:
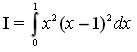
Câu 3: (1 điểm)
a) Từ một hộp đựng 4 viên bi đỏ và 5 viên bi xanh, chọn ngẫu nhiên hai viên bi. Tính xác suất để hai viên bi được chọn cùng màu.
b) Giải phương trình: (1/3)x-1 - (1/9)x = 2
Câu 4: (1 điểm) Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2; 1; -1) và mặt phẳng (P): x + 2y – 2z + 3 = 0. Viết phương trình đường thẳng d đi qua A và vuông góc với (P). Tìm tọa độ điểm M thuộc đường thẳng d sao cho 3OM = √3.
Câu 5 (1 điểm) Cho hình chóp SABCD có đáy là hình vuông, SA vuông góc với đáy, SA = a. Góc giữa đường thẳng SD và mặt phẳng (SAC) bằng 300. Tính thể tích khối chóp SABCD và khoảng cách từ điểm D đến mặt phẳng (SBM), (M là trung điểm CD).
Câu 6 (1 điểm) Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC có trực tâm H(3; 0) và trung điểm của BC là I(6; 1). Đường thẳng AH có phương trình x + 2y – 3 = 0. Gọi D, E lần lượt là chân đường cao kẻ từ B và C của tam giác ABC. Xác định tọa độ các đỉnh của tam giác ABC, biết phương trình đường thẳng DE là x - 2 = 0 và điểm D có tung độ dương.
Câu 7 (1 điểm) Giải hệ phương trình
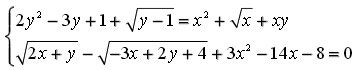
Câu 8 (1 điểm) Cho ba số không âm a, b, c thỏa mãn ab + bc + ac = 1. Chứng minh rằng:
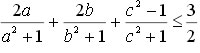
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1: ( 2 điểm)
a. Hàm số y = x3 – 3x2 +1
TXĐ D = R
Sự biến thiên:
| lim y | = -∞ | lim y | = +∞ |
| x→-∞ | x→+∞ |
y’ = 3x2 - 6x => y’ = 0 ↔ x = 0; x = 2
BBT
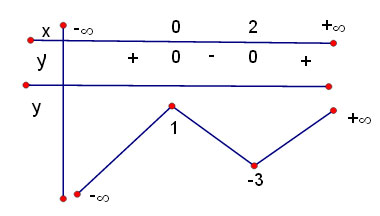
Hàm số đồng biến trên (-∞; 0) và (2; +∞); Hàm số nghịch biến trên (0;2).
Hàm số đạt cực đại tại x = 0; y = 1; đạt cực tiểu tại x = 2; y = -3
Đồ thị
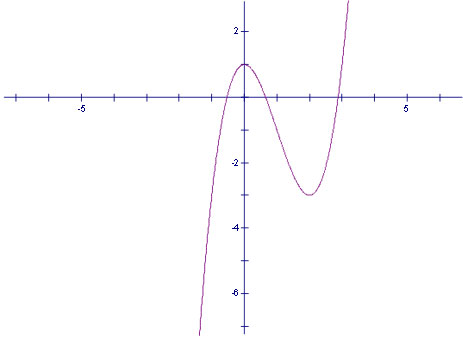
b. Ta có y’ = 3x2 - 6mx => y’ = 0 ↔ x = 0 hoặc x = 2m
Với m ≠ 0 hàm số có hai điểm cực trị A(0;m); B( 2m; -4m3); AB = √[4m2(1 + 4m2)]
Phương trình đường thảng AB: 2m2x + y – m = 0; Diện tích tam giác OAB: SOAB = 1/2 d(O; AB)AB = 4
![]()
↔ m = ±2 (TM)
Câu 2: (2 điểm)
a. sin 2x - cos2x = 2sinx - 1 ↔ sinx(sinx + cosx - 1) = 0
↔ sinx = 0 hoặc sinx + cosx - 1 = 0
↔ x = kπ hoặc x = k2π; x = π/2 + k2π
↔ x = kπ hoặc x = π/2 + k2π
b. 1,0 điểm