Thi thử THPT quốc gia tại TP. HCM: Đề thi, đáp án môn Toán năm 2015
Đề thi thử THPT Quốc gia môn Toán năm 2015 Sở GD-ĐT Thành phố Hồ Chí Minh là đề thi thử đại học môn Toán mới ra đề ngày 11/05/2015, mà VnDoc cập nhật xin được giới thiệu đến các bạn tham khảo. Đây là đề thi có chất lượng dành cho các bạn làm đề thi thử luyện thi đại học môn Toán được chắc chắn nhất.
Đề thi thử THPT Quốc gia môn Toán năm 2015 trường THPT Thủ Đức, Hồ Chí Minh
Đề thi thử THPT Quốc gia môn Toán lần 3 năm 2015 trường THPT Quỳnh Lưu 1, Nghệ An
Đề thi thử THPT Quốc gia 2015 môn Ngữ Văn trường THPT An Mỹ, Bình Dương
Đề thi thử Quốc gia môn Toán
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC |
KÌ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2015 Đề thi môn: Toán Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1. (2,0 điểm) Cho hàm số: y = (2x-1)/(x-2)
a, Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b, Tìm m để đường thẳng (d): y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4√2.
Câu 2. (1,0 điểm)
a, Giải phương trình: 16 sin²x/2 - cos2x = 15.
b, Cho số phức z thỏa mãn phương trình:
| _ | ||
| (1 - i)z + (2 + i) | z | = 4 + i |
Tìm mô đun của z.
Câu 3. (0,5 điểm) Giải phương trình: log2² x = log2x/4 + 4.
Câu 4. (0,5 điểm) Giải hệ phương trình:
| { | (√y + 1)² + y²/x = y² + 2√(x - 2) |
| x + (x - 1)/y + y/x = y² + y |
Câu 5. (1,0 điểm) Tính tích phân
| 4 | |||
| I = | ∫ | √x - 4lnx | dx |
| x² | |||
| 1 |
Câu 6 (1,0 điểm) Cho hình chóp S.ABC có SC = (a√70)/5, đáy ABC là tam giác vuông tại A, AB 2a,AC a = = và hình chiếu của S lên mặt phẳng (ABC) là trung điểm cạnh AB. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng BC và SA.
Câu 7 (1,0 điểm) Trong mặt phẳng Oxy, gọi H(3; -2), I(8;11),K(4;-1) lần lượt là trực tâm, tâm đường tròn ngoại tiếp, chân đường cao vẽ từ A của tam giác ABC. Tìm tọa độ các điểm A, B, C.
Câu 8 (1,0 điểm) Trong không gian Oxyz, cho 3 điểm A(2;1;-1),B(1; 3;1),C(1;2; 0). Viết phương trình đường thẳng (d) qua A, vuông góc và cắt đường thẳng BC.
Câu 9 (0,5 điểm) Gọi X là tập hợp các số tự nhiên gồm năm chữ số đôi một khác nhau được tạo thành từ các số 1,2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ tập hợp X. Tính xác suất để số được chọn có tổng các chữ số là một số lẻ.
Câu 10 (1,0 điểm) Cho hai số thực x, y thỏa mãn điều kiện: x4 + 16x4 + 2(2xy - 5)² = 41.
Tìm giá trị nhỏ nhất và lớn nhất của biểu thức P = xy - 3/(x² + 4y² + 3)
Hết
Họ và tên thí sinh:...............................................................Số báo danh:........................................
Đáp án đề thi thử Quốc gia môn Toán
Câu 1:
a) TXĐ: D = R\{2}
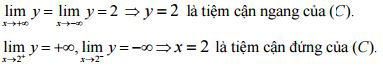
y' = -3/(x - 2)²
Ta có y' < 0 với mọi x thuộc D suy ra hàm số giảm trên các khoảng (-∞, 2), (2, +∞).
Vẽ đồ thị, đồ thị nhận I(2,2) làm tâm đối xứng
b, Phương trình hoành độ giao điểm của (C) và (d) là:
(2x - 1)/(x - 2) = x + m ↔ x² + (m - 4)x + 1 - 2m = 0 (*)
Δ = m² + 12 > 0 với mọi m suy ra Phương trình (*) luôn có 2 nghiệm phân biệt x1, x2 với mọi m và
- x1 + x2 = 4 - m
- x1.x2 = 1 - 2m
AB = 4√2 ↔ √((x1 + x2)² + (y1 + y2)²) = 4√2.
Tương đương (4 - m)² - 4(1 - 2m)² = 16 → m² = 4 → m = ± 2.



