Đề thi thử THPT Quốc gia lần 1 năm 2015 môn Toán trường THPT Chuyên Võ Nguyên Giáp, Quảng Bình
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia lần 1 năm 2015 môn Toán trường THPT Chuyên Võ Nguyên Giáp, Quảng Bình là đề thi thử đại học môn Toán có đáp án, là tài liệu ôn thi môn Toán THPT rất tốt dành cho các bạn học sinh và thầy cô tham khảo, luyện thi đại học môn Toán khối A, B, D.
Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 4
Đề thi minh họa và đáp án kỳ thi THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Thanh Chương 3, Nghệ An
|
TRƯỜNG THPT CHUYÊN VÕ NGUYÊN GIÁP
|
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015 LẦN THỨ NHẤT Môn TOÁN Thời gian làm bài: 180 phút, không kể phát đề |
Câu 1 (2,0 điểm). Cho hàm số: y = 1/3 x3 + 2x2 + 3x - 1.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến với đồ thị (C) tại giao điểm của (C) với đường thẳng y = -1.
Câu 2 (1,0 điểm)

Câu 6 (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình thang cân (BC//AD). Biết đường cao SH = a, với H là trung điểm của AD, AB = BC = CD = a, AD = 2a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB và AD theo a.
Câu 7. (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD. Gọi H là hình chiếu vuông góc của B lên AC, M và N lần lượt là trung điểm của AH và BH, trên cạnh CD lấy K sao cho MNCK là hình bình hành. Biết M(9/5; 2/5), K(9; 2) và các đỉnh B, C lần lượt nằm trên các đường thẳng 2x - y + 2 = 0 và y - x - 5 = 0, hoành độ đỉnh C lớn hơn 4. Tìm tọa độ các đỉnh của hình chữ nhật ABCD.
Câu 8 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho hai điểm M(1; -2; 3), N( -1; 0; 1) và mặt phẳng (P): x + y + z + 4 = 0. Viết phương trình mặt cầu (S) có bán kính bằng MN/6, tâm nằm trên đường thẳng MN và (S ) tiếp xúc với (P).
Câu 9 (0,5 điểm). Trong kì thi TN THPT, Bình làm đề thi trắc nghiệm môn Hóa học. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng; trả lời đúng mỗi câu được 0,2 điểm. Bình trả lời hết các câu hỏi và chắc chắn đúng 45 câu; 5 câu còn lại Bình chọn ngẩu nhiên. Tính xác suất để điểm thi môn Hóa học của Bình không dưới 9,5 điểm.
Câu 10 (1,0 điểm). Cho các số thực dương a, b thỏa mãn: a4 + b4 + 1/ab ≤ ab + 2. Chứng minh rằng:
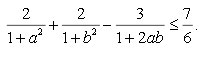
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1 (2,0 điểm)
a. 1,0 điểm
TXĐ: D = R
Giới hạn:
| lim y | = -∞ | lim y | = +∞ |
| x→-∞ | x→+∞ |
Đồ thị không có tiệm cận
y' = x2 + 4x + 3, ∀x ∈ R; y' = 0 ↔ x = -1 hoặc x = -3.
Bảng biến thiên
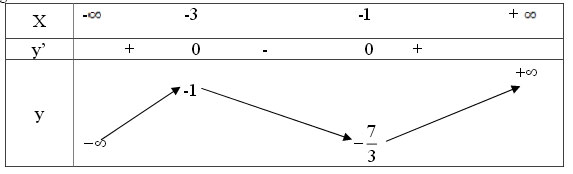
Hàm số đồng biến trên các khoảng (-∞; -3) và (-1; +∞), nghịch biến trên khoảng (-3; -1).
Hàm số đạt cực tiểu tại x = -1 và f(-1) = -7/3; hàm số đạt cực đại tại x = -3 và f(-3) = -1.
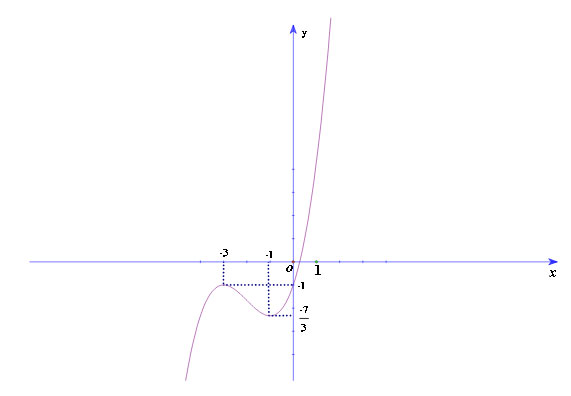
Đồ thị
b. 1,0 điểm
Hoành độ giao điểm của đồ thị (C) với đường thẳng y = -1 là nghiệm của phương trình 1/3 x3 + 2x2 + 3x - 1 = -1.
Giải phương trình ta được nghiệm x = 0 và x = -3
Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 0 là y = 3x -1.
Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng -3 là y = -1.
Câu 2 (1,0 điểm)
a. 0,5 điểm
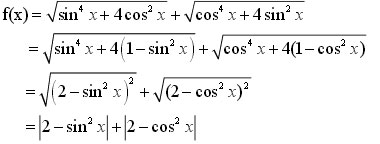
Vì -1 ≤ sinx, cos ≤ -1, ∀x ∈ R nên f(x) = 2 - sin2x + 2 - cos2x = 3, ∀x ∈ R → f'(x) = 0, ∀x ∈ R.
Mời các bạn tải file đầy đủ về tham khảo!


