Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2015 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2015 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp là đề thi thử đại học môn Toán có chất lượng, là tài liệu hay giúp các bạn thử sức trước các kì thi quan trọng sắp tới. Mời các bạn cùng tham khảo.
Đề thi thử THPT Quốc gia môn Vật lý lần 2 năm 2015 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp
Đề thi thử THPT Quốc gia môn Sinh học lần 2 năm 2015 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp
Đề thi thử THPT Quốc gia môn Hóa học lần 2 năm 2015 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp
| SỞ GD & ĐT ĐỒNG THÁP THPT Chuyên Nguyễn Quang Diêu | ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015 - LẦN 2 MÔN: TOÁN Thời gian làm bài: 180 phút (Không kể thời gian giao đề) |
Câu 1 (2,0 điểm). Cho hàm số y = x4 - 2x2 + 4 (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
b) Tìm các giá trị của tham số m để phương trình x2(x2 - 2) + 3 - m có 2 nghiệm phân biệt.
Câu 2 (1,0 điểm).
a) Cho góc α thỏa mãn π < α < 3π/2 và sinα = −4/5. Tính A = (1 + cotα) / (1 - cotα)
b) Cho số phức z thỏa mãn 
. Tính môđun của số phức z.
Câu 3 (0,5 điểm). Giải phương trình 22 + x - 22 - x = 15.
Câu 4 (1,0 điểm). Giải hệ phương trình
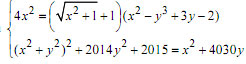
Câu 5 (1,0 điểm). Tính tích phân 
Câu 6 (1,0 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. AB = 3a, BC = 5a; mặt phẳng (SAC) vuông góc với mặt phẳng (ABC). Biết SA= 2a√3 và góc SAC = 300. Tính theo a thể tích của khối chóp S.ABC và khoảng cách từ điểm A đến mặt phẳng (SBC)
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành ABCD có D(5;4). Đường trung trực của đoạn DC có phương trình d1: 2x + 3y - 9 = 0 và đường phân giác trong góc BAC của tam giác ABC có phương trình d2: 5x + y + 10 = 0. Xác định tọa độ các đỉnh còn lại của hình bình hành.
Câu 8 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(–1; 1; 2), B(0; 1; 1), C(1; 0; 4) và đường thẳng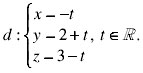 
. Viết phương trình mặt phẳng (ABC) và tìm tọa độ giao điểm của d với mặt phẳng (ABC).
Câu 9 (0,5 điểm). Cho số nguyên dương n thỏa mãn điều kiện Cnn + Cn-1n + 1/2 A2n = 821. Tìm hệ số của x31 trong khai triển Niu-tơn của (x + 1/x2)n (x ≠ 0).
Câu 10 (1,0 điểm). Cho x, y là các số thực dương thỏa mãn x + y ≤ 1. Tìm giá trị nhỏ nhất của biểu thức
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1 (2,0 điểm)
a. Tập xác định D = R
Chiều biến thiên:
- Ta có y' = 4x(x2 - 1); y' = 0 ↔ x = 0 hoăc x = ±1.
- Hàm số nghịch biến trên mỗi khoảng (-∞; -1) và (0; 1).
- Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; +∞)
Cực trị:
- Hàm số đạt cực tiểu tại x = ±1, yCT = y(±1) = 3.
- Hàm số đạt cực đại tại x = 0, yCĐ = y(0) = 4.
Các giới hạn tại vô cực:
| lim y | = +∞ | lim y | = -∞ |
| x→-∞ | x→+∞ |
Bảng biến thiên
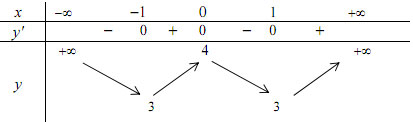
Đồ thị hàm số: Đồ thị qua các điểm A(-1/√3; 31/9), B(-2; 12), C(2; 12).
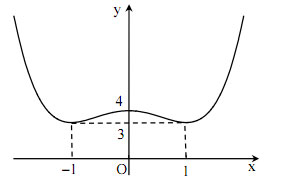
b. Ta có x2(x2 - 2) + 3 - m ↔ x4 - 2x2 + 3 - m ↔ x4 - 2x2 + 4 - m + 1 (*)
Số nghiệm của PT (*) bằng số giao điểm của đường thẳng d: y = m - 1 với đồ thị (C).
Dựa vào đồ thị (C), để PT đã cho có 2 nghiệm thì: m + 1 > 4 hoặc m + 1 = 3
Hay m > 3 hoặc m = 2
Vậy PT đã cho có 2 nghiệm khi m > 3 hoặc m = 2.
Câu 2 (1,0 điểm)
a. Ta có cos2α = 1 - sin2α = 1 - 16/25 = 9/25 cosα = -3/5 (do π < α < 3π/2)
Từ đó có A = (sinα + cosα) / (sinα - cosα) = (-4/5 - 3/5) / (14/5 + 3/5) =7.
b. Đặt z = a + bi (a, b ϵ R). Khi đó
↔ 3(a + bi + 1) = 4(a - bi) + 1 + 7i ↔ a - 2 + 7(1 - b)i = 0
↔ a = 2, b = 1 → |z| = 5.
