Đề thi thử THPT Quốc gia năm 2015 môn Toán Sở GD - ĐT Quảng Nam
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia năm 2015 môn Toán Sở GD - ĐT Quảng Nam có đáp án là đề thi thử môn Toán năm có đáp án đi kèm. Đây là tài liệu ôn thi THPT Quốc gia 2016 hữu ích dành cho các bạn, giúp các bạn tự thử sức trước các kì thi quan trọng sắp tới. Mời các bạn cùng tham khảo.
Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Quảng Nam
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Lào Cai
Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Chuyên Nguyễn Bỉnh Khiêm, Quảng Nam
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Sư phạm Hà Nội (Lần 3)
| SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG NAM |
KỲ THI THỬ THPT QUỐC GIA NĂM 2015 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1. (2,0 điểm) Cho hàm số y = x3 - 3x2.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Tìm m để đường thẳng y = mx cắt đồ thị (C) tại ba điểm phân biệt.
Câu 2. (1,0 điểm)
a) Cho góc α thỏa mãn 0 < α < π/4 và sinα + cosα = √5/2. Tính sinα - cosα.
b) Tìm số phức z biết rằng ![]()
Câu 3. (0.5 điểm) Giải phương trình 2log22(x - 3) + log2(x - 3) = 1.
Câu 4. (1,0 điểm) Giải phương trình 2x3 + 9x2 - 6x(1 + 2√(6x - 1)) + 2√(6x - 1) + 8 = 0.
Câu 5. (1,0 điểm) Tính tích phân: 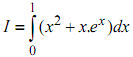
Câu 6. (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, với AB = 2a, AD = a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ điểm D đến mặt phẳng (SBC).
Câu 7. (1.0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A, có B(-2; 1) và C(8; 1). Đường tròn nội tiếp tam giác ABC có bán kính r = 3√5 - 5. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết tung độ điểm I là số dương.
Câu 8. (1.0 điểm) Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + y - z + 6 = 0. Viết phương trình mặt cầu có tâm K(0; 1; 2) và tiếp xúc với mặt phẳng (P). Viết phương trình mặt phẳng chứa trục Oy và vuông góc với mặt phẳng (P).
Câu 9. (0.5 điểm) Một hộp chứa 20 quả cầu giống nhau được ghi số từ 1 đến 20. Chọn ngẫu nhiên 5 quả cầu từ hộp đó, tính xác suất để 5 quả cầu được chọn ra có 3 quả ghi số lẻ và 2 quả ghi số chẵn, trong đó có đúng một quả ghi số chia hết cho 4.
Câu 10. (1.0 điểm) Cho ba số thực dương a; b; c tùy ý. Tìm giá trị nhỏ nhất của biểu thức:
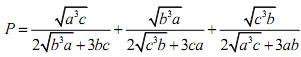
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1. (2,0 điểm)
a. 1,0 điểm
- Tập xác định: D = R
Giới hạn:
| lim y | = +∞ | lim y | = -∞ |
| x→+∞ | x→+∞ |
- Sự biến thiên y’ = 3x2 - 6x
y’ = 0 ↔ x = 0 hoặc x = 2
Hàm số nghịch biến trên khoảng (0;2), đồng biến trên mỗi khoảng (-∞;0), (2;+∞).
Hàm số đạt cực đại tại x = 0, giá trị cực đại: y(0) = 0.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu: y(2)= -4.
Bảng biến thiên
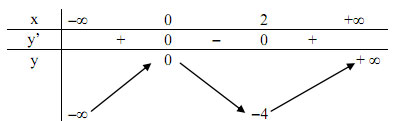
- Đồ thị:
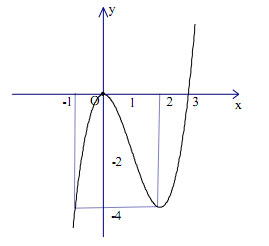
b. 1,0 điểm
Phương trình hoành độ giao điểm của (C) và đường thẳng y = mx là: x3 - 3x2 = mx
↔ x(x2 - 3x - m) = 0 ↔ x = 0 hoặc x2 - 3x - m = 0 (*)
Đường thẳng y = mx cắt đồ thị (C) tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt khác 0, tức là:
| { | Δ > 0 | ↔ { | 9 + 4m > 0 | ↔ m > -9/4 và m ≠ 0 |
| m ≠ 0 | m ≠ 0 |
Câu 2. (1,0 điểm)
a. Ta có: (sinα - cosα)2 + (sinα + cosα)2 = 2(sin2α + cos2α) = 2
→ (sinα - cosα)2 = 2 - (sinα + cosα)2 = 2 - 5/4 = 3/4 → sinα -cosα = ±3/2
Do 0 < α < π/4 → 0 < sinα < cosα → sinα - cosα < 0 nên chọn sinα - cosα = -3/2.
b. Đặt z = a + bi (a, b ϵ Z) → ![]()
Khi đó: ![]()
↔ a + bi + 2(a - bi) = 6 + 2i
↔ a + bi + 2a - 2bi = 6 2i
↔ 3a - bi = 6 + 2i
↔ 3a = 6 và -b = 2 ↔ a = 2 và b = -2 → z = 2 - 2i


