Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2015 trường THPT Chuyên Long An, Long An
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2015 trường THPT Chuyên Long An, Long An có đáp án là đề thi thử đại học môn Toán hữu ích dành cho các bạn tham khảo, luyện đề. Hi vọng tài liệu này giúp các bạn tự ôn tập kiến thức, thử sức trước các kì thi quan trọng sắp tới hiệu quả hơn.
Đề thi thử THPT Quốc gia môn Hóa học lần 2 năm 2015 trường THPT Chuyên Long An, Long An
Bộ đề thi thử THPT Quốc gia 2015 môn Tiếng Anh trường THPT Chuyên Long An
Đề thi thử THPT Quốc gia môn Ngữ văn lần 2 năm 2015 trường THPT Chuyên Long An, Long An
| SỞ GIÁO DỤC VÀ ĐÀO TẠO LONG AN TRƯỜNG THPT CHUYÊN LONG AN |
ĐỀ THI THỬ THPTQG LẦN 2 - NĂM HỌC 2014-2015 Môn: Toán. Thời gian làm bài: 180 phút (không kể thời gian phát đề) |
| Câu 1. (2,0 điểm). Cho hàm số | y = | x - 2 | (C) |
| 2x - 1 |
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b. Viết phương trình tiếp tuyến của (C), biết tiếp tuyến song song với đường thẳng d: y = 5x - 2.
Câu 2. (1,0 điểm).
a. Chứng minh rằng: 3(sin8x - cos8x) + 4(cos6x - 2sin6x) + 6sin4x = 1.
b. Tìm phần thực và phần ảo của số phức z thỏa mãn: (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i.
Câu 3. (0,5 điểm). Giải bất phương trình: 22x - 5.2x + 6 ≤ 0.
| Câu 4. (1,0 điểm). Giải hệ phương trình: | { | 2x(x2 + 3y2) = 7 |
| x2 + 6xy + y2 = 5x + 3y |
| Câu 5. (1,0 điểm). Tính tích phân: | 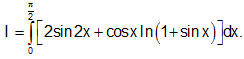 |
Câu 6. (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB; Góc giữa đường thẳng SC và mặt phẳng đáy bằng 600. Tính theo a thể tích khối chóp S.ABCD và góc giữa hai đường thẳng SB và AC.
Câu 7. (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trung tuyến và phân giác trong kẻ từ cùng một đỉnh B có phương trình lần lượt là d1: 2x + y - 3 = 0 và d2: x + y - 2 = 0. Điểm M(2; 1) thuộc đường thẳng AB, đường tròn ngoại tiếp tam giác ABC có bán kính bằng √5. Biết đỉnh A có hoành độ dương, hãy xác định tọa độ các đỉnh của tam giác ABC.
Câu 8. (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):; x - 2y + 2z - 1 = 0, (Q): x + y - 2x + 1 = 0 và điểm I(1; 1; -2). Viết phương trình mặt cầu (S) tâm I, tiếp xúc với (P) và phương trình mặt phẳng (α) vuông góc với (P), (Q) sao cho khoảng cách từ I đến (α) bằng √29.
Câu 9. (0,5 điểm). Trong một bình có 2 viên bi trắng và 8 viên bi đen. Người ta bốc 2 viên bi bỏ ra ngoài rồi bốc tiếp một viên bi thứ ba. Tính xác suất để viên bi thứ ba là bi trắng.
Câu 10. (1,0 điểm). Cho hai số dương x, y phân biệt thỏa mãn: x2 + 2y = 12. Tìm giá trị nhỏ nhất của biểu thức
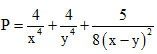
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1. (2,0 điểm)
a. Tập xác định: D = R\{-1/2}
Giới hạn và tiệm cận:
| lim y | = +∞ | lim y | = -∞ | Suy ra TCĐ: x = -1/2 |
| x→(-1/2)- | x→(-1/2)+ |
| lim y | = lim y | = 1/2 | Suy ra TCN: x = 1/2 | |
| x→+∞ | x→-∞ | |||
Sự biến thiên: y' = 5/(2x + 1) > 0, ∀x ϵ D
Suy ra hàm số đồng biến trên mỗi khoảng (-∞; -1/2) và (-1/2; +∞)
Hàm số không có cực trị (có thể bỏ ý này)
Bảng biến thiên
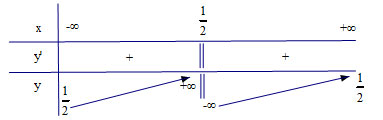
Bảng giá trị, vẽ đúng đồ thị, có nhận xét.
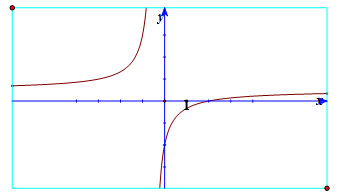
b) Gọi M(a; (a - 2)/(2a + 1)) là tiếp điểm (a ≠ -1/2). Tiếp tuyến song song với đường thẳng nên suy ra: y'(a) = 5.
Giải được a = 0 hoặc a = -1
- a = 0: Phương trình tiếp tuyến là: y = 5x - 2 (loại vì trùng d)
- a = -1: Phương trình tiếp tuyến là: y = 5x + 8 (nhận)
Vậy: y = 5x + 8
Câu 2. (1,0 điểm).
a. 3(sin8x - cos8x) + 4(cos6x - 2sin6x) + 6sin4x = 1.
VT = 3(sin4x + cos4x)(sin2x + cos2x) + 4(cos6x - 2sin6x) + 6sin4x
VT = 3sin6x - 3sin4xcos2x + 3cos4sin2x - 3cos6x + 4cos6x - 8sin6x + 6sin4x
VT = -5sin6x + cos6x - 3sin4x(1 - sin2x) + 3cos4x(1 - cos2x) + 6sin4x
VT = 3(sin4x + cos4x) - 2(sin6x + cos6x)
VT = 3(1 - 2sin2x cos2x) - 2(1 - 3sin2x.cos2x) = 1
b. Tìm được z = 1/2 + 3/2i
Phần thực: a = 1/2. Phần ảo: b = 3/2.


