VnDoc.com

Vòng tròn lượng giác

Đường tròn lượng giác

Vòng tròn lượng giác và cách sử dụng vòng tròn lượng giác

1. Góc lượng giác và số đo góc lượng giác
2. Vòng tròn lượng giác và hướng dẫn sử dụng vòng tròn lượng giác
2. Dấu của các giá trị lượng giác
3. Bảng giá trị lượng giác từ đến
4. Công thức các cung liên kết trên đường tròn lượng giác
5. Bài tập vận dụng vòng tròn lượng giác
Tài liệu học tập SGK Ngữ văn lớp 10 Mới

VnDoc.com xin giới thiệu tới quý thầy cô và các bạn học sinh tài liệu tham khảo Vòng tròn lượng giác để bạn đọc cùng tham khảo và có thêm tài liệu học tập nhé.

1. Góc lượng giác và số đo góc lượng giác

a) Góc lượng giác

Cho hai tia Ou, Ov.

Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ tia Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov. Kí hiệu: (Ou, Ov).

Minh họa

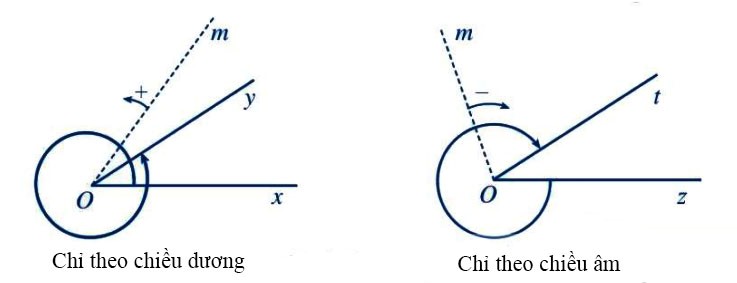
Chú ý:

Khi tia Om quay góc a⁰ thì góc lượng giác mà tia đó quét được có số đo a⁰, (tương tự với rad).

Nếu góc lượng giác (Ou, Ov) có số đo a⁰ thì ta kí hiệu sđ(Ou, Ov) = a hoặc (Ou, Ov) = a.

Mỗi một góc lượng giác gốc O xác định bởi tia đầu Ou và tia cuối Ov và số đo của góc đó.

Minh họa:

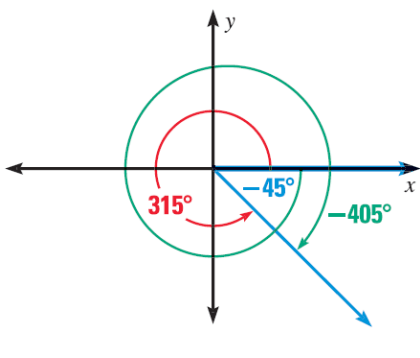
b) Tính chất của góc lượng giác

Cho hai góc lượng giác (Ou, Ov); (O’u’, O’v’) có tia đầu trùng nhau (Ou ≡ O’u’) tia cuối trùng nhau (Ov≡ O’v’). Khi đó nếu sử dụng đơn vị đo là độ thì ta nói:

$(O u, O v) = (O^{'} u^{'}, O^{'} v^{'}) + k {.360}^{0}, (k \in Z)$

Nếu sử dụng đơn vị đo là radian thì công thức trên có thể viết như sau:

$(O u, O v) = (O^{'} u^{'}, O^{'} v^{'}) + k 2 π, (k \in Z)$

Với ba tia tùy ý $O u, O v, O w$ ta có:

$(Ou,Ov) + (Ov,Ow) = (Ou,Ow) + k2\pi,\left( k\mathbb{\in Z} \right)$ $(O u, O v) + (O v, O w) = (O u, O w) + k 2 π, (k \in Z)$

Ví dụ: Cho góc lượng giác (Ou, Ov) có số đo $\frac{\pi}{5}$ $\frac{π}{5}$ . Hỏi trong các góc $\frac{6\pi}{5};\frac{9\pi}{5};\frac{- 11\pi}{5};\frac{31\pi}{5};\frac{- 14\pi}{5}$ $\frac{6 π}{5}; \frac{9 π}{5}; \frac{- 11 π}{5}; \frac{31 π}{5}; \frac{- 14 π}{5}$ những góc nào có số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho?

Hướng dẫn giải

Ta có:

$\frac{6\pi}{5} = \pi + \frac{\pi}{5}$ $\frac{6 π}{5} = π + \frac{π}{5}$

$\frac{9\pi}{5} = 2\pi - \frac{\pi}{5}$ $\frac{9 π}{5} = 2 π - \frac{π}{5}$

$\frac{- 11\pi}{5} = - 2\pi - \frac{\pi}{5}$ $\frac{- 11 π}{5} = - 2 π - \frac{π}{5}$

$\frac{31\pi}{5} = 6\pi + \frac{\pi}{5}$ $\frac{31 π}{5} = 6 π + \frac{π}{5}$

$\frac{- 14\pi}{5} = - 3\pi + \frac{\pi}{5}$ $\frac{- 14 π}{5} = - 3 π + \frac{π}{5}$

Nhận thấy số đo của một góc lượng giác có tia đầu và tia cuối với góc đã cho khi ta quay góc đó chẵn 1 vòng mà 1 vòng có số đo $2\pi$ $2 π$

Suy ra những góc thỏa mãn yêu cầu đề bài là $\frac{9\pi}{5};\frac{- 11\pi}{5};\frac{31\pi}{5}$ $\frac{9 π}{5}; \frac{- 11 π}{5}; \frac{31 π}{5}$ .

2. Vòng tròn lượng giác và hướng dẫn sử dụng vòng tròn lượng giác

Vòng tròn lượng giác

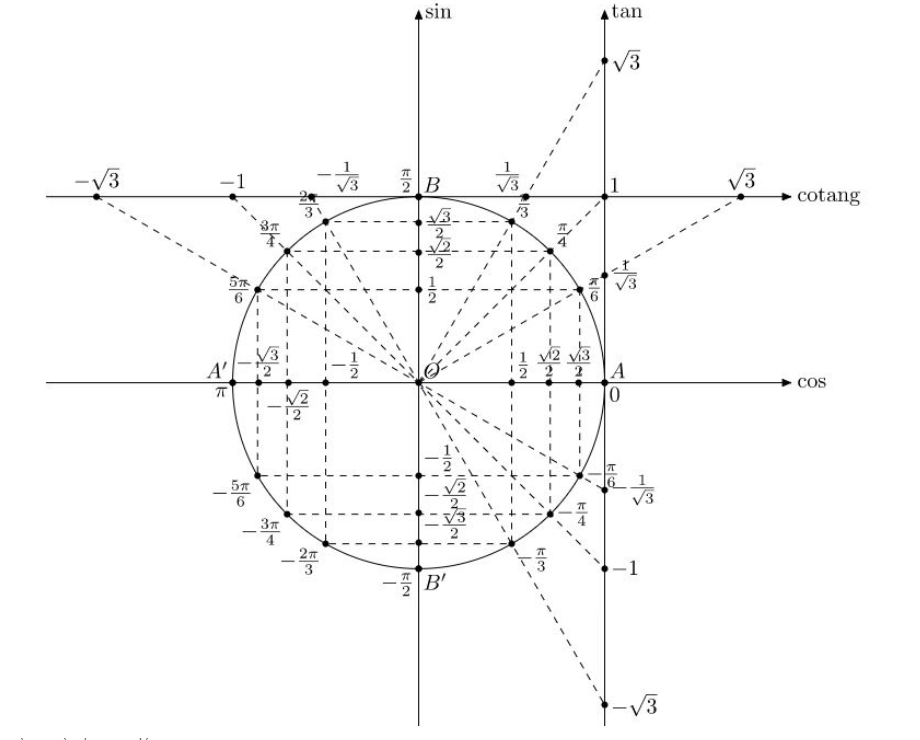
Vòng tròn lượng giác cơ bản đầy đủ chi tiết

- Vòng tròn lượng giác là đường tròn đơn vị tâm O bán kính 1, định hướng với quy ước chiều dương là chiều ngược chiều kim đồng hồ và trên đó A là điểm gốc.

- Điểm _{$P (x, y)$} trên đường tròn lượng giác sao cho một điểm C bất kì nằm trên đường tròn ta đều có _{$(O A, O C) = α$} được gọi là điểm trên đường tròn lượng giác biểu diễn cung lượng giác có số đo _$α$.

- Trục Ox được gọi là trục giá trị cos.

- Trục Oy được gọi là trục giá trị sin.

- Trục tan có gốc là điểm và vuông góc với trục cos, trục cotan có gốc là điểm vuông góc với trục sin.

Ví dụ: Xác định điểm P trên đường tròn lượng giác sao cho $(OA;OP) = \frac{5\pi}{4}$ $(O A; O P) = \frac{5 π}{4}$ .

Hướng dẫn giải

Gọi điểm M là điểm chính giữa của cung A’B’ trên đường tròn lượng giác.

Ta có: $(OA;OP) = \frac{5\pi}{4}$ $(O A; O P) = \frac{5 π}{4}$ được biểu diễn như hình vẽ sau:

2. Dấu của các giá trị lượng giác

Góc phần tư số	I	II	III	IV
Giá trị lượng giác	I	II	III	IV
sin x	+	+	-	-
cos x	+	-	-	+
tan x	+	-	+	-
cot x	+	-	+	-

Ví dụ: Xét dấu các giá trị lượng giác $\alpha = \frac{5\pi}{6}$ $α = \frac{5 π}{6}$ .

Hướng dẫn giải

Giả sử điểm M trên đường tròn lượng giác sao cho $\alpha = \frac{5\pi}{6}$ $α = \frac{5 π}{6}$

Do $\frac{\pi}{2} < \frac{5\pi}{6} < \pi$ $\frac{π}{2} < \frac{5 π}{6} < π$ nên điểm M thuộc góc phần tư thứ II.

Do đó $\left\{ \begin{matrix} \sin\left( \frac{5\pi}{6} \right) > 0;cos\left( \frac{5\pi}{6} \right) < 0 \\ \tan\left( \frac{5\pi}{6} \right) < 0;cot\left( \frac{5\pi}{6} \right) < 0 \\ \end{matrix} \right.$ ${\begin{matrix} \sin (\frac{5 π}{6}) > 0; c o s (\frac{5 π}{6}) < 0 \\ \tan (\frac{5 π}{6}) < 0; c o t (\frac{5 π}{6}) < 0 \end{matrix}$

Ví dụ: Tính giá trị biểu thức: $A = tan^{2}\frac{\pi}{3} + sin^{2}\frac{\pi}{4} + \cot\frac{\pi}{4} + \cos\frac{\pi}{2}$ $A = t a n^{2} \frac{π}{3} + s i n^{2} \frac{π}{4} + \cot \frac{π}{4} + \cos \frac{π}{2}$

Hướng dẫn giải

Ta có:

$A = tan^{2}\frac{\pi}{3} + sin^{2}\frac{\pi}{4} + \cot\frac{\pi}{4} + \cos\frac{\pi}{2}$ $A = t a n^{2} \frac{π}{3} + s i n^{2} \frac{π}{4} + \cot \frac{π}{4} + \cos \frac{π}{2}$

$= \left( \sqrt{3} \right)^{2} + \left( \frac{\sqrt{2}}{2} \right)^{2} + 1 + 0 = 3 + \frac{1}{2} + 1 = \frac{9}{2}$ $= {(\sqrt{3})}^{2} + {(\frac{\sqrt{2}}{2})}^{2} + 1 + 0 = 3 + \frac{1}{2} + 1 = \frac{9}{2}$

3. Bảng giá trị lượng giác từ _$0^{0}$ đến _$180^{0}$

$\alpha$ $α$	$0$ $\left( {{0}^{0}} \right)$ $(0^{0})$	$\frac{\pi }{6}$ $\frac{π}{6}$ $\left( {{30}^{0}} \right)$ $(30^{0})$	$\frac{\pi }{4}$ $\frac{π}{4}$ $\left( {{45}^{0}} \right)$ $(45^{0})$	$\frac{\pi }{3}$ $\frac{π}{3}$ $\left( {{60}^{0}} \right)$ $(60^{0})$	$\frac{\pi }{2}$ $\frac{π}{2}$ $\left( {{90}^{0}} \right)$ $(90^{0})$	$\frac{2\pi }{3}$ $\frac{2 π}{3}$ $\left( {{120}^{0}} \right)$ $(120^{0})$	$\frac{3\pi }{4}$ $\frac{3 π}{4}$ $\left( {{135}^{0}} \right)$ $(135^{0})$	$\frac{5\pi }{6}$ $\frac{5 π}{6}$ $\left( {{150}^{0}} \right)$ $(150^{0})$	$\pi$ $π$ $\left( {{180}^{0}} \right)$ $(180^{0})$	$\frac{3\pi }{2}$ $\frac{3 π}{2}$ $\left( {{270}^{0}} \right)$ $(270^{0})$	$2\pi$ $2 π$ $\left( {{360}^{0}} \right)$ $(360^{0})$
$\sin \alpha$ $\sin α$	0	$\frac{1}{2}$ $\frac{1}{2}$	$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$1$	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$	$\frac{1}{2}$ $\frac{1}{2}$	0	-1	0
$\cos \alpha$ $\cos α$	1	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$	$\frac{1}{2}$ $\frac{1}{2}$	0	$-\frac{1}{2}$ $- \frac{1}{2}$	$-\frac{\sqrt{2}}{2}$ $- \frac{\sqrt{2}}{2}$	$-\frac{\sqrt{3}}{2}$ $- \frac{\sqrt{3}}{2}$	-1	0	1
$\tan \alpha$ $\tan α$	0	$\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$ $\sqrt{3}$	\|\|	$-\sqrt{3}$ $- \sqrt{3}$	-1	$-\frac{1}{\sqrt{3}}$ $- \frac{1}{\sqrt{3}}$	0	\|\|	0
$\cot \alpha$ $\cot α$	\|\|	$\sqrt{3}$ $\sqrt{3}$	1	$\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$	0	$-\frac{1}{\sqrt{3}}$ $- \frac{1}{\sqrt{3}}$	-1	$-\sqrt{3}$ $- \sqrt{3}$	\|\|	0	\|\|

4. Công thức các cung liên kết trên đường tròn lượng giác

Góc đối nhau ( cos đối)	Góc bù nhau (sin bù)	Góc phụ nhau (Phụ chéo)	Góc hơn kém (Khác pi tan)
cos (-α) = cos α	sin (π-α) = sin α	sin (π/2-α)= cos α	sin (π+α) = - sin α
sin (-α) = -sin α	cos (π-α) = - cos α	cos (π/2-α) = sinα	cos (π+α) = - cosα
tan (-α) = - tan α	tan (π-α) = - tan α	tan (π/2-α) = cot α	tan (π+α) = tanα
cot (-α) = -cot α	cot (π-α) = – cot α	cot (π/2-α) = tan α	cot (π+α) = cotα

Ví dụ: Rút gọn các biểu thức sau:

a) $M = \cos\left( a + \frac{\pi}{2} \right) + \cos(2\pi - a) + \cos(3\pi + a)$ $M = \cos (a + \frac{π}{2}) + \cos (2 π - a) + \cos (3 π + a)$

b) $N = \cos(5\pi - x) - \sin\left( \frac{3\pi}{2} + x \right) + \tan\left( \frac{3\pi}{2} - x \right) + \cos(3\pi - x)$ $N = \cos (5 π - x) - \sin (\frac{3 π}{2} + x) + \tan (\frac{3 π}{2} - x) + \cos (3 π - x)$

Hướng dẫn giải

a) $M = \cos\left( a + \frac{\pi}{2} \right) + \cos(2\pi - a) + \cos(3\pi + a)$ $M = \cos (a + \frac{π}{2}) + \cos (2 π - a) + \cos (3 π + a)$

$M = - \sin x + \cos( - x) - \cos x$ $M = - \sin x + \cos (- x) - \cos x$

$M = - \sin x + \cos x - \cos x$ $M = - \sin x + \cos x - \cos x$

$M = - \sin x$ $M = - \sin x$

b) $N = \cos(5\pi - x) - \sin\left( \frac{3\pi}{2} + x \right) + \tan\left( \frac{3\pi}{2} - x \right) + \cot(3\pi - x)$ $N = \cos (5 π - x) - \sin (\frac{3 π}{2} + x) + \tan (\frac{3 π}{2} - x) + \cot (3 π - x)$

$N = \cos(4\pi + \pi - x) - \sin\left( \pi + \frac{\pi}{2} + x \right) + \tan\left( \pi + \frac{\pi}{2} - x \right) + \cot(2\pi + \pi - x)$ $N = \cos (4 π + π - x) - \sin (π + \frac{π}{2} + x) + \tan (π + \frac{π}{2} - x) + \cot (2 π + π - x)$

$N = \cos(\pi - x) + \sin\left( + \frac{\pi}{2} + x \right) + \tan\left( \frac{\pi}{2} - x \right) + \cot(\pi - x)$ $N = \cos (π - x) + \sin (+ \frac{π}{2} + x) + \tan (\frac{π}{2} - x) + \cot (π - x)$

$N = - \cos x + \cos x + \cot x + - \cot x = 0$ $N = - \cos x + \cos x + \cot x + - \cot x = 0$

5. Bài tập vận dụng vòng tròn lượng giác

Câu 1: Trên đường tròn lượng giác, số các điểm ngọn của cung có số đo bằng $\frac{\pi }{6} + \frac{{k2\pi }}{5}$ $\frac{π}{6} + \frac{k 2 π}{5}$ là:

A. 2

B. 3

C. 5

D. 6

Câu 2: Trên đường tròn lượng giác, điểm ngọn của cung có số đo 3000⁰ nằm ở góc phần tư thứ mấy?

A. I

B. II

C. III

D. IV

Câu 3: Cho góc α biết $\pi < \alpha < \frac{{3\pi }}{2}$ $π < α < \frac{3 π}{2}$ , chọn đáp án đúng trong các đáp án dưới đây?

A. cos α > 0, sin α > 0	B. cos α > 0, sin α < 0
C. cos α < 0, sin α > 0	D. cos α < 0, sin α < 0

Câu 4: Trên đường tròn lượng giác cho các cung lượng giác (I), (II), (III) và (IV) có điểm đầu là A và có số đo lần lượt là:

(a) $\frac{\pi }{4}$

\frac{π}{4}

(b) $- \frac{{7\pi }}{4}$

- \frac{7 π}{4}

(c) $\frac{{13\pi }}{4}$

\frac{13 π}{4}

(d) $- \frac{{71\pi }}{4}$

- \frac{71 π}{4}

Hỏi các cung nào có điểm cuối trùng nhau?

A. Chỉ (a) và (b)	B. Chỉ (a), (b), (c)
C. Chỉ (b), (c), (d)	D. Chỉ (a), (b) và (d)

Câu 5: Biết một góc lượng giác (Ou, Ov) có số đo $\frac{{ - 138\pi }}{5}$ $\frac{- 138 π}{5}$ . Góc lượng giác (Ou, Ov) âm lớn nhất là:

A. -1,6π

B. -27,6π

C. -0,6π

D. -0,4π

Tài liệu học tập SGK Ngữ văn lớp 10 Mới

-------------------------------------------------------------------

Trên đây VnDoc đã chia sẻ đến các bạn học sinh Vòng tròn lượng giác nhằm cung cấp cơ sở kiến thức ôn tập cho các bạn học sinh, giúp các bạn tiếp xúc với nhiều dạng bài về hàm số lượng giác. Bài viết cho chúng ta thấy được khái niệm vòng tròn lượng giác và hướng dẫn sử dụng vòng tròn lượng giác, dấu của giá trị lượng giác, bảng giá trị lượng giác, bên cạnh đó còn có các bài tập vận dụng... Hi vọng qua bài viết bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10 nhé. Chúc các bạn ôn tập thật tốt!

Mời bạn đọc tham khảo thêm một số tài liệu liên quan đến bài học:

Chia sẻ, đánh giá bài viết

7

39.351

Chia sẻ bởi:
Nguyễn Thị Huê

Tải về

Chọn file muốn tải về:

Vòng tròn lượng giác

364,4 KB

Tải xuống Word
326 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Gợi ý cho bạn

Xem thêm

Vật lý lớp 12

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Giáo án Steam 3 - 4 tuổi

Giáo án Steam 4 - 5 tuổi

Giáo án Steam 5 - 6 tuổi

Tranh tô màu

Trường mầm non

Tiền tiểu học

Danh mục Trường Tiểu học

Dạy con học ở nhà

Sáng kiến kinh nghiệm

Giáo án Mầm non

Giáo án Lớp nhà trẻ

Giáo án Lớp mầm

Giáo án Lớp chồi

Giáo án Lớp lá

Giáo án Chương trình đổi mới

Thư viện Đề thi

Bài tập cuối tuần

Trắc nghiệm

Sách Cánh diều

Sách Chân trời sáng tạo

Sách Kết nối tri thức

Tài liệu Giáo viên

Học Toán Trực Tuyến

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 2

Môn Tiếng Việt lớp 2

Chuyên đề - Văn mẫu

Môn Tiếng Anh

Môn Đạo Đức

Tự Nhiên & Xã Hội

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 3

Môn Tiếng Việt lớp 3

Chuyên đề - Văn mẫu

Tiếng Anh lớp 3

Đạo Đức lớp 3

Tự nhiên xã hội lớp 3

Tin Học lớp 3

Âm Nhạc lớp 3

Công nghệ lớp 3

Hoạt động trải nghiệm lớp 3

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 4