Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Công thức mạch dao động LC

Công thức Vật lý 12

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Vật Lý

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Tổng hợp công thức mạch dao động LC

Trong chuyên đề mạch dao động của chương trình Vật lý 12, việc nắm vững hệ thống công thức là yếu tố then chốt giúp học sinh giải nhanh các dạng bài dao động điện từ. Từ tần số dao động riêng, chu kỳ, năng lượng điện – từ cho đến mối quan hệ giữa điện tích, cường độ dòng điện và điện dung… tất cả đều được quy chuẩn bằng các công thức quan trọng. Bài viết này sẽ giúp bạn tổng hợp đầy đủ công thức mạch dao động theo cách dễ nhớ, dễ áp dụng, đồng thời phù hợp cho quá trình ôn thi, đặc biệt là trong các đề kiểm tra và đề thi THPT Quốc gia.

A. Mạch dao động

Hình vẽ minh họa:

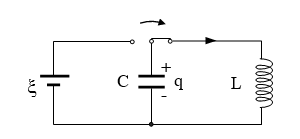
Cuộn cảm có độ tự cảm L mắc nối tiếp với tụ điện C thành mạch điện kín.

B. Dao động điện từ tự do trong mạch dao động

1. Biến thiên điện tích và dòng điện

Công thức tính điện tích

$q = Q_{0}\cos(\omega t + \varphi)(C)$ $q = Q_{0}\cos(\omega t + \varphi)(C)$

Công thức tính cường độ dòng điện

$\left\{ \begin{matrix}i = \omega Q_{0}\cos(\omega t + \varphi + \frac{\pi}{2}) =I_{0}\cos(\omega t + \varphi + \frac{\pi}{2})\ \\I_{0} = \omega Q_{0} = \omega CU_{0} = U_{0}\sqrt{\frac{C}{L}}\end{matrix} \right.$ $\left\{ \begin{matrix}i = \omega Q_{0}\cos(\omega t + \varphi + \frac{\pi}{2}) =I_{0}\cos(\omega t + \varphi + \frac{\pi}{2})\ \\I_{0} = \omega Q_{0} = \omega CU_{0} = U_{0}\sqrt{\frac{C}{L}}\end{matrix} \right.$ với $\omega = \sqrt{\frac{1}{LC}}$ $\omega = \sqrt{\frac{1}{LC}}$

Dòng điện qua L biến thiên điều hòa sớm pha hơn điện tích trên tụ điện C góc $\frac{\pi}{2}$ $\frac{\pi}{2}$

Pha ban đầu $\varphi$ $\varphi$

Tìm $\varphi$ $\varphi$ bằng cách giải hệ phương trình $\left\{ \begin{matrix} q_{0} = Q_{0}\cos\varphi \\ i_{0} = - \omega Q_{0}\sin\varphi \end{matrix} \right.\ \ khi\ t_{0} = 0$ $\left\{ \begin{matrix} q_{0} = Q_{0}\cos\varphi \\ i_{0} = - \omega Q_{0}\sin\varphi \end{matrix} \right.\ \ khi\ t_{0} = 0$

Phương trình độc lập với thời gian: $\left\{ \begin{matrix} q^{2} + \frac{i^{2}}{\omega^{2}} = Q_{0}^{2}\ \\ \frac{u^{2}}{L^{2}\omega^{4}} + \frac{i^{2}}{\omega^{2}} = Q_{0}^{2}\ \\ u^{2}C^{2} + \frac{i^{2}}{\omega^{2}} = Q_{0}^{2} \end{matrix} \right.$ $\left\{ \begin{matrix} q^{2} + \frac{i^{2}}{\omega^{2}} = Q_{0}^{2}\ \\ \frac{u^{2}}{L^{2}\omega^{4}} + \frac{i^{2}}{\omega^{2}} = Q_{0}^{2}\ \\ u^{2}C^{2} + \frac{i^{2}}{\omega^{2}} = Q_{0}^{2} \end{matrix} \right.$

2. Chu kỳ và tần số riêng của mạch dao động

$T = 2\pi\sqrt{LC}$ $T = 2\pi\sqrt{LC}$ và $f = \frac{1}{2\pi\sqrt{LC}}$ $f = \frac{1}{2\pi\sqrt{LC}}$

Máy phát hoặc máy thu sóng điện từ sử dụng mạch dao động LC thì tần số sóng điện từ phát hoặc thu được bằng tần số riêng của mạch.

Bước sóng của sóng điện từ thu được $\lambda = 2\pi.c\sqrt{LC}$ $\lambda = 2\pi.c\sqrt{LC}$

$C_{1}ntC_{2} \rightarrow T = \sqrt{\frac{{T_{1}}^{2}.T_{2}^{2}}{T_{1}^{2} + T_{2}^{2}}} \rightarrow \lambda = \sqrt{\frac{\lambda_{1}^{2}.\lambda_{2}^{2}}{\lambda_{1}^{2} + \lambda_{2}^{2}}} \rightarrow f = \sqrt{f_{1}^{2} + f_{2}^{2}}$ $C_{1}ntC_{2} \rightarrow T = \sqrt{\frac{{T_{1}}^{2}.T_{2}^{2}}{T_{1}^{2} + T_{2}^{2}}} \rightarrow \lambda = \sqrt{\frac{\lambda_{1}^{2}.\lambda_{2}^{2}}{\lambda_{1}^{2} + \lambda_{2}^{2}}} \rightarrow f = \sqrt{f_{1}^{2} + f_{2}^{2}}$

$C_{1}//C_{2} \rightarrow T = \sqrt{T_{1}^{2} + T_{2}^{2}} \rightarrow \lambda = \sqrt{\lambda_{1}^{2} + \lambda_{2}^{2}} \rightarrow f = \sqrt{\frac{f_{1}^{2}.f_{2}^{2}}{f_{1}^{2} + f_{2}^{2}}}$ $C_{1}//C_{2} \rightarrow T = \sqrt{T_{1}^{2} + T_{2}^{2}} \rightarrow \lambda = \sqrt{\lambda_{1}^{2} + \lambda_{2}^{2}} \rightarrow f = \sqrt{\frac{f_{1}^{2}.f_{2}^{2}}{f_{1}^{2} + f_{2}^{2}}}$

C. Năng lượng điện từ

Tổng năng lượng điện trường trên tụ điện và năng lượng tử trường trên cuộn cảm gọi là năng lượng điện từ

Năng lượng điện trường $W_{đ} = \frac{q^{2}}{2C} = \frac{1}{2}Cu^{2}$ $W_{đ} = \frac{q^{2}}{2C} = \frac{1}{2}Cu^{2}$
Năng lượng từ trường $W_{t} = \frac{1}{2}Li^{2}$ $W_{t} = \frac{1}{2}Li^{2}$
Năng lượng điện từ trường $W = W_{đ} + W_{t} = \frac{Q_{0}^{2}}{2C} = \frac{C.U_{0}^{2}}{2} = \frac{LI_{0}^{2}}{2}$ $W = W_{đ} + W_{t} = \frac{Q_{0}^{2}}{2C} = \frac{C.U_{0}^{2}}{2} = \frac{LI_{0}^{2}}{2}$

Lưu ý:

+ Năng lượng điện từ trường không đổi.

+ Năng lượng điện trường và năng lượng từ trường biến thiên tuần hoàn theo thời gian với chu kỳ T/2, tần số 2f.

+ Cứ sau thời gian $\frac{T}{4}$ $\frac{T}{4}$ năng lượng điện lại bằng năng lượng từ.

+ Hệ thức liên hệ $I_{0} = U_{0}\sqrt{\frac{C}{L}}$ $I_{0} = U_{0}\sqrt{\frac{C}{L}}$

+ Dao động của R,L,C là dao động cưỡng bức với “lực cưỡng bức” là hiệu điện thế U_AB. Hiện tượng cộng hưởng xảy ra khi Z_L=Z_C.

+ Công suất cần cung cấp để mạch không bi tắt dần bằng công suất tỏa nhiệt:

$P = I^{2}R = \frac{\omega^{2}C^{2}U_{0}^{2}}{2}R = \frac{U_{0}^{2}RC}{2L}$ $P = I^{2}R = \frac{\omega^{2}C^{2}U_{0}^{2}}{2}R = \frac{U_{0}^{2}RC}{2L}$

---------------------------------------------------

Hy vọng bảng tổng hợp công thức mạch dao động trong bài viết đã giúp bạn có thêm tài liệu học tập ngắn gọn nhưng đầy đủ để ghi nhớ và vận dụng hiệu quả trong quá trình giải bài tập Vật lý 12. Việc nắm chắc các công thức nền tảng sẽ tạo cơ sở vững chắc cho bạn khi làm bài kiểm tra, ôn thi học kỳ hoặc đặc biệt là trong kỳ thi THPT Quốc gia. Đừng quên lưu lại tài liệu, chia sẻ cho bạn bè và luyện tập thường xuyên để phát huy tối đa hiệu quả. Chúc bạn học tốt và ngày càng tự tin với môn Vật lý!

Tải về

Chọn file muốn tải về: