Toàn bộ công thức dòng điện xoay chiều trong đoạn mạch R, L, C

 Công thức Vật lý 12: Dòng điện xoay chiều trong mạch RLC

Bạn đang ôn thi THPT Quốc gia môn Vật lý và muốn tìm một tài liệu tổng hợp toàn bộ công thức dòng điện xoay chiều trong đoạn mạch R, L, C đầy đủ – dễ hiểu – học nhanh? Đây chính là bài viết bạn cần! Trong chương trình Vật lý 12, chuyên đề mạch RLC xoay chiều là một trong những phần có tần suất ra đề cao nhất, đòi hỏi học sinh nắm chắc công thức về điện trở, cảm kháng, dung kháng, công suất, hệ số công suất, độ lệch pha và các dạng bài nâng cao.

A. Đoạn mạch chỉ có điện trở thuần R

u_R cùng pha với i, (ϕ = ϕ_u – ϕ_i = 0) và \(I = \frac{U}{R}\) và \(I_{0} = \frac{U_{0}}{R}\)

Lưu ý: Điện trở R cho dòng điện không đổi đi qua và có \(I = \frac{U}{R}\)

B. Đoạn mạch chỉ có cuộn thuần cảm L

u_L nhanh pha hơn i là π/2, (ϕ = ϕ_u – ϕ_i = π/2)

\(I = \frac{U}{Z_{L}}\) và \(I_{0} = \frac{U_{0}}{Z_{L}}\) với Z_L = ωL là cảm kháng

Lưu ý: Cuộn thuần cảm L cho dòng điện không đổi đi qua hoàn toàn (không cản trở).

C. Đoạn mạch chỉ có tụ điện C

u_C chậm pha hơn i là π/2, (ϕ = ϕ_u – ϕ_i = -π/2)

\(I = \frac{U}{Z_{C}}\) và \(I_{0} = \frac{U_{0}}{Z_{C}}\) với \(Z_{C} = \frac{1}{\omega C}\) là dung kháng

Lưu ý: Tụ điện C không cho dòng điện không đổi đi qua (cản trở hoàn toàn).

D. Đặc điểm đoạn mạch thuần RLC nối tiếp

a. Tổng trở: \(Z = \sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}\)

b. Độ lệch pha (u so với i): \(\tan\varphi = \frac{Z_{L} - Z_{C}}{R} = \frac{U_{L} - U_{C}}{U_{R}}\) \(\Rightarrow \left\{ \begin{matrix} Z_{L} > Z_{C}:\ u\ som\ pha\ hon\ i \\ Z_{L} = Z_{C}:\ u\ cung\ pha\ voi\ i \\ Z_{L} < Z_{C}:\ u\ tre\ pha\ hon\ i\ \ \end{matrix} \right.\)

c. Định luật Ohm: \(I_{0} = \frac{U_{0}}{Z};\ I = \frac{U}{Z}\)

d. Công suất tiêu thụ trên đoạn mạch: \(P = UI\cos\varphi\), hệ số công suất \(\cos\varphi = \frac{R}{Z} = \frac{U_{R}}{U}\)

Chú ý: Với mạch hoặc chỉ chứa L, hoặc chỉ chứa C, hoặc chứa LC không tiêu thụ công suất (\(P = 0\))

Nếu \(i = I_{0}\cos\omega t\ thì\ u = U_{0}cos(\omega t + \varphi)\)

Nếu \(u = U_{0}\cos\omega t\ thì\ i = I_{0}cos(\omega t - \varphi)\)

\(\varphi_{\frac{u}{i}} = \varphi_{u} - \varphi_{i} = - \varphi_{\frac{i}{u}}\)

e. Giản đồ vectơ 

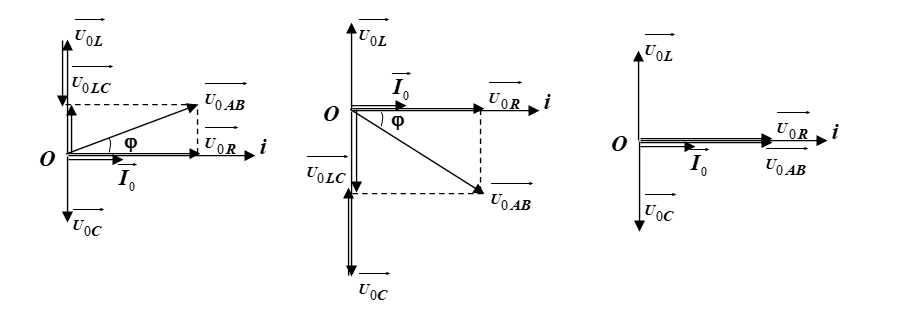
Ta có: \(\left\{ \begin{matrix} u = u_{R} + u_{L} + u_{C} \\ \overrightarrow{U_{0}} = \overrightarrow{U_{0R}} + \overrightarrow{U_{0L}} + \overrightarrow{U_{0C}} \end{matrix} \right.\)

f. Liên hệ giữa các hiệu điện thế hiệu dụng trong đoạn mạch thuần RLC nối tiếp

Từ \(Z = \sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}\)suy ra \(U = \sqrt{U_{R}^{2} + (U_{L} - U_{C})^{2}}\)

Tương tự \(Z_{RL} = \sqrt{R^{2} + Z_{L}^{2}}\) suy ra \(U_{RL} = \sqrt{U_{R}^{2} + U_{L}^{2}}\)

Tương tự \(Z_{RC} = \sqrt{R^{2} + Z_{C}^{2}}\) suy ra \(U_{RC} = \sqrt{U_{R}^{2} + U_{C}^{2}}\)

\(Z_{LC} = \left| Z_{L} - Z_{C} \right|\) suy ra \(U_{LC} = \left| U_{L} - U_{C} \right|\)

g. Công suất toả nhiệt trên đoạn mạch RLC

• Công suất tức thời: P = UIcosϕ + UIcos(2ωt + ϕ)
• Công suất trung bình: P = UIcosϕ = I²R.

Điện áp u = U₁ + U₀cos(ωt + ϕ) được coi gồm một điện áp không đổi U₁ và một điện áp xoay chiều u=U₀cos(ωt + ϕ) đồng thời đặt vào đoạn mạch.

Tần số dòng điện do máy phát điện xoay chiều một pha có P cặp cực, rôto quay với vận tốc n vòng/giây phát ra: f = pn Hz.

• Từ thông gửi qua khung dây của máy phát điện Φ:

\(\Phi = NBScos(\omega t + \varphi) = \Phi_{0}cos(\omega t + \varphi)\ (Wb)\)

• Suất điện động tức thời: \(e = - \frac{d\Phi}{dt} = - \Phi'\); \(e = \omega NBSsin(\omega t + \varphi)\ (V) = E_{0}sin(\omega t + \varphi)\)

\(e = E_{0}sin(\omega t + \varphi) = E_{0}cos(\omega t + \varphi - \frac{\pi}{2})\)= ωNSBcos(ωt + ϕ - \(\frac{\pi}{2}\)); \(\sin\alpha = cos(\alpha - \frac{\pi}{2})\)

• Hiệu điện thế tức thời: \(u = U_{0}cos(\omega t + \varphi_{u})\).
• Nếu máy phát có điện trở rất nhỏ thì: U₀ = E₀.

Với Φ₀ = NBS là từ thông cực đại, N là số vòng dây, B là cảm ứng từ của từ trường, S là diện tích của vòng dây, ω = 2πf, E₀ = ωNSB là suất điện động cực đại.

E. Đoạn mạch RLC có L thay đổi

* Khi \(L = \frac{1}{\omega^{2}C}\) thì I_Max ⇒ U_Rmax; P_Max còn U_LCMin

Lưu ý: L và C mắc liên tiếp nhau

* Khi \({\overrightarrow{U}}_{RC}\bot\overrightarrow{U} \Rightarrow \tan\varphi_{RC}.tan\varphi = - 1\) hay \(Z_{L} = \frac{R^{2} + Z_{C}^{2}}{Z_{C}}\) thì \(U_{LMax} = \frac{U\sqrt{R^{2} + Z_{C}^{2}}}{R}\)

* Với L = L₁ hoặc L = L₂ thì U_L có cùng giá trị thì U_Lmax khi

\(\frac{1}{Z_{L}} = \frac{1}{2}(\frac{1}{Z_{L_{1}}} + \frac{1}{Z_{L_{2}}}) \Rightarrow L = \frac{2L_{1}L_{2}}{L_{1} + L_{2}}\)

* Với L = L₁ hoặc L = L₂ thì I, U_R, P có cùng giá trị thì \(Z_{L1} - Z_{c} = - Z_{L2} + Z_{C} \rightarrow Z_{C} = \frac{Z_{L1} + Z_{L2}}{2}\)

* Khi \(Z_{L} = \frac{Z_{C} + \sqrt{4R^{2} + Z_{C}^{2}}}{2}\) thì \(U_{RLMax} = \frac{2UR}{\sqrt{4R^{2} + Z_{C}^{2}} - Z_{C}}\)

Lưu ý: R và L mắc liên tiếp nhau

Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu!

--------------------------------------------------------

Với bộ tổng hợp công thức dòng điện xoay chiều trong đoạn mạch R, L, C ở trên, bạn hoàn toàn có thể tự tin xử lý mọi dạng bài từ cơ bản đến nâng cao trong đề thi THPT Quốc gia môn Vật lý. Hãy lưu lại bài viết, ghi nhớ các công thức trọng tâm và luyện tập thường xuyên để đạt hiệu quả tối đa. Đừng quên rằng: nắm chắc công thức là bước đầu, nhưng hiểu cách áp dụng mới là chìa khóa giúp bạn “ăn trọn điểm” phần mạch xoay chiều. Chúc bạn học tốt, tối ưu thời gian ôn luyện và đạt kết quả cao trong kỳ thi sắp tới!