Công thức giải bài toán hộp kín (bài toán hộp đen)
Bài toán hộp đen Vật lý 12
Trong chương trình Vật lý 12, dạng bài hộp kín (hay còn gọi là bài toán hộp đen) là một trong những dạng bài tập đặc trưng của phần mạch điện xoay chiều. Đây là dạng toán đòi hỏi khả năng phân tích, suy luận từ các dữ kiện đầu vào như điện áp, cường độ dòng điện, hệ số công suất… để xác định cấu trúc bên trong của hộp kín gồm các phần tử R, L, C. Vì tính tư duy cao, dạng bài này thường xuất hiện trong các đề thi học kỳ và đặc biệt là đề thi THPT Quốc gia.
Cách tìm phần tử trong hộp đen
1. Mạch điện đơn giản

a. Nếu ![]() \(U_{NB}\) cùng pha với
\(U_{NB}\) cùng pha với ![]() \(i\) suy ra
\(i\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(R_{0}\)
\(R_{0}\)
b. Nếu ![]() \(U_{NB}\) sớm pha với
\(U_{NB}\) sớm pha với ![]() \(i\) góc
\(i\) góc ![]() \(\frac{\pi}{2}\) suy ra
\(\frac{\pi}{2}\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(L_{0}\)
\(L_{0}\)
c. Nếu ![]() \(U_{NB}\) trễ pha với
\(U_{NB}\) trễ pha với ![]() \(i\) góc
\(i\) góc ![]() \(\frac{\pi}{2}\) suy ra
\(\frac{\pi}{2}\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(C_{0}\)
\(C_{0}\)
2. Mạch điện phức tạp
a. Mạch 1
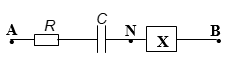
Nếu ![]() \(U_{AB}\) cùng pha với
\(U_{AB}\) cùng pha với ![]() \(i\) suy ra
\(i\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(L_{0}\)
\(L_{0}\)
Nếu ![]() \(U_{AN}\) và
\(U_{AN}\) và ![]() \(U_{NB}\) tạo với nhau góc
\(U_{NB}\) tạo với nhau góc ![]() \(\frac{\pi}{2}\) suy ra
\(\frac{\pi}{2}\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(R_{0}\)
\(R_{0}\)
Vậy ![]() \(\boxed{x}\) chứa
\(\boxed{x}\) chứa ![]() \(\left( R_{0},L_{0} \right)\)
\(\left( R_{0},L_{0} \right)\)
b. Mạch 2
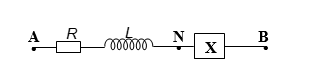
Nếu ![]() \(U_{AB}\) cùng pha với
\(U_{AB}\) cùng pha với ![]() \(i\) suy ra
\(i\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(C_{0}\)
\(C_{0}\)
Nếu ![]() \(U_{AN}\) và
\(U_{AN}\) và ![]() \(U_{NB}\) tạo với nhau góc
\(U_{NB}\) tạo với nhau góc ![]() \(\frac{\pi}{2}\) suy ra
\(\frac{\pi}{2}\) suy ra ![]() \(\boxed{x}\) chỉ chứa
\(\boxed{x}\) chỉ chứa ![]() \(R_{0}\)
\(R_{0}\)
Vậy ![]() \(\boxed{x}\) chứa
\(\boxed{x}\) chứa ![]() \(\left( R_{0},C_{0} \right)\)
\(\left( R_{0},C_{0} \right)\)
------------------------------------------
Dạng bài toán hộp kín (hộp đen) trở nên đơn giản hơn rất nhiều khi bạn nắm chắc công thức, hiểu nguyên lý hoạt động của các phần tử RLC và biết cách phân tích dựa trên số liệu đề bài. Hy vọng bài viết đã cung cấp cho bạn hệ thống kiến thức rõ ràng, dễ hiểu và đầy đủ nhất để tự tin xử lý mọi dạng bài trong chương Vật lý 12.











