VnDoc.com

Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số

Tóm tắt lý thuyết Toán 12 chương 1

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Lý thuyết Sự đồng biến, nghịch biến của hàm số

A. Sự đồng biến, nghịch biến của hàm số
- 1. Tính đơn điệu của hàm số
- 2. Tính đơn điệu và dấu của đạo hàm
B. Các dạng bài tập xét tính đơn điệu của hàm số
- Dạng 1: Xét tính đơn điệu của hàm số lớp 12
- Dạng 2: Tìm điều kiện của tham số để hàm số đơn điệu
C. Bài tập tự rèn luyện xét tính đơn điệu của hàm số

Trong chương trình Toán 12, chương 1 là nền tảng quan trọng của giải tích, với trọng tâm là sự đồng biến và nghịch biến của hàm số. Đây là kiến thức cốt lõi, không chỉ phục vụ việc khảo sát và vẽ đồ thị hàm số mà còn được ứng dụng rộng rãi trong nhiều chuyên đề khác như cực trị, tiệm cận hay ứng dụng tích phân. Việc nắm chắc khái niệm đồng biến – nghịch biến, hiểu rõ cách xét dấu đạo hàm và vận dụng linh hoạt vào bài tập sẽ giúp học sinh học tốt các phần kiến thức tiếp theo.

Trong bài viết “Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số”, chúng ta sẽ cùng hệ thống hóa công thức, trình bày phương pháp giải chi tiết và tóm tắt lý thuyết một cách ngắn gọn, dễ hiểu. Đây là tài liệu hữu ích cho học sinh lớp 12 đang trong quá trình học tập cũng như ôn luyện cho kỳ thi THPT quốc gia môn Toán.

A. Sự đồng biến, nghịch biến của hàm số

1. Tính đơn điệu của hàm số

- Cho K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói

+ Hàm số đồng biến (tăng) trên K nếu mọi cặp x₁,x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x1) nhỏ hơn f(x₂), tức là x₁ < x₂ => f(x₁) < f(x₂)

+ Hàm số nghịch biến (giảm) trên K nếu với mọi cặp x₁,x₂ thuộc K mà x₁ < x₂ thì f(x1) nhỏ hơn f(x₂), tức là x₁ < x₂ => f(x₁₎ > f(x₂)

- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K, K được gọi chung là khoảng đơn điệu của hàm số.

Nhận xét: Hàm số đồng biến trên K thì đồ thị hàm số đi lên từ trái sang phải. Hàm số nghịch biến trên K thì đồ thị hàm số đi xuống từ trái sang phải.

2. Tính đơn điệu và dấu của đạo hàm

- Giả sử hàm số y = f(x) có đạo hàm trên khoảng (a;b). Khi đó:

+ Nếu f'(x) ≥ 0, ∀x ∈ (a; b) và f'(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên (a;b).

+ Nếu f'(x) ≤ 0, ∀x ∈ (a; b) và f'(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên (a;b).

Ghi chú: Dấu bằng xảy ra chỉ tại một số hữu hạn điểm.

B. Các dạng bài tập xét tính đơn điệu của hàm số

Dạng 1: Xét tính đơn điệu của hàm số lớp 12

Bài toán xét tính đơn điệu của hàm số không hề phức tạp. Học sinh chỉ cần hiểu rõ kiến thức là có thể làm được bài. Vì vậy, trước khi đi sâu vào phương pháp, công thức giải nhanh dạng bài tập này, VnDoc sẽ điểm qua một số kiến thức trọng tâm.

Hàm số y = f(x) xác định trên I, I là một khoảng, một đoạn hay một nửa khoảng.

– Hàm số y = f(x) được gọi là đồng biến trên I nếu:

∀ x1, x2 ∈ I: x1 < x2 ⇔ f(x1) < f(x2).

– Hàm số y = f (x) được gọi là nghịch biến trên I nếu:

∀ x1, x2 ∈ I: x1 < x2 ⇔ f(x1) > f(x2).

Hàm số đồng biến, nghịch biến được gọi chung là hàm số đơn điệu trên I.

Phương pháp giải dạng bài xét tính đơn điệu của hàm số lớp 12

Để giải dạng bài tập này, các bạn cần thực hiện đủ các bước sau:

– Tìm tập xác định D.

– Tìm f'(x). Tìm các điểm mà f'(xi)=0 và f'(xi) không xác định.

– Lập bảng biến thiên.

– Kết luật khoảng đồng biến, nghịch biến.

Ví dụ: Xét hàm số y = f(x) = x³ – 3x + 1.

Tập xác định D = R

Ta có f'(x) = 3x² -3. f'(x) = 0 ⇔ x= 1; hoặc x= -1.

Thay x = -2, f'(x) = 9 >0.

Thay x = 0. f'(x) = -3 < 0.

Ta có bảng biến thiên sau:

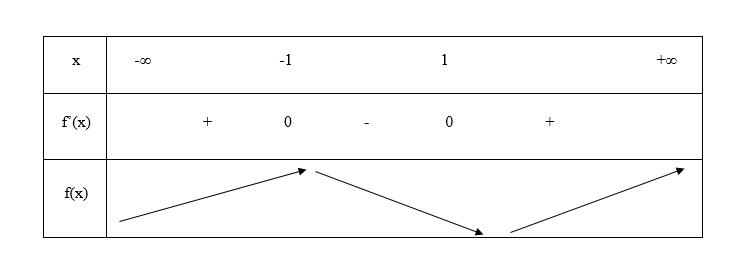Bảng biến thiên của hàm số

Từ bảng biến thiên kết luận:

– Hàm số đồng biến trên khoảng (- ∞; -1) và (1;+∞)

– Hàm số nghịch biến trên khoảng (-1;1).

Giải bài toán xét tính đơn điệu của hàm số bằng máy tính cầm tay:

Ngoài cách sử dụng bảng biến thiên để giải bài tập xét tính đơn điệu của hàm số lớp 12, học sinh cũng có thể dùng chiếc casio của mình để giải.

Ví dụ: Cho hàm số y = x4 -2x2 + 4. Mệnh đề nào dưới đây là đúng?

A. Hàm số đồng biến trên khoảng (- ∞; -1).

B. Hàm số nghịch biến trên khoảng (- ∞; -1) và (1;+∞).

C. Hàm số nghịch biến trên khoảng (- ∞; -1) và ( 0;1).

D. Hàm số đồng biến trên khoảng (-1;1).

Chúng ta có thể dùng máy tính để xét tính đơn điệu như nhau:

Nhập MODE 7, nhập f(x) = x4 -2x2 + 4 Start?-5 → End?5→ Step?1. Khi đó ta nhận được bảng giá trị.

x	F(x)	x	F(x)
-5	579	0	4
-4	228	1	-3
-3	67	2	12
-2	12	3	67
-1	-3	4	228
		5	579

Từ bảng giá trị ta thấy hàm số nghịch biến trên (- ∞; -1) và (0;1).

Trên đây là ví dụ cơ bản nhất về bài tập xét tính đơn điệu của hàm số lớp 12. Từ phương pháp giải dạng bài tập trên, các em có thể vận dụng giải nhiều bài tập khác.

Vi dụ. Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}$ $\mathbb{R}$ và có bảng biến thiên như hình bên dưới

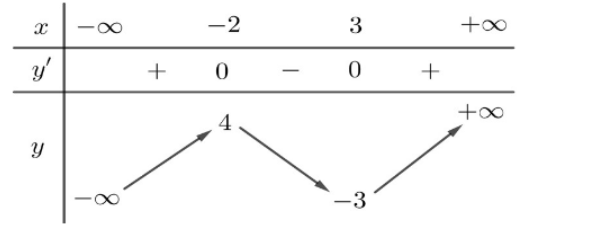
Hàm số $y = f(x)$ đồng biến trên khoảng nào dưới đây?

Hướng dẫn giải:

Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên $(3; + \infty)$ $(3; + \infty)$.

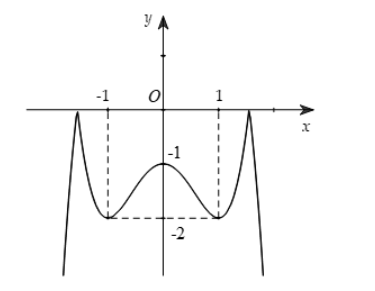
Ví dụ. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

Hướng dẫn giải:

Dựa vào đồ thị ta có hàm số đồng biến trên khoảng $( - 1;\ 0).$ $( - 1;\ 0).$

Ví dụ. Cho hàm số $y = \frac{{2x + 1}}{{ - x + 1}}$ $y = \frac{{2x + 1}}{{ - x + 1}}$. Mệnh đề nào dưới dây là đúng?

A. Hàm số đồng biến trên $\mathbb{R}\backslash \left\{ 1 ight\}$ $\mathbb{R}\backslash \left\{ 1 ight\}$

B. Hàm số nghịch biến trên $\mathbb{R}\backslash \left\{ 1 ight\}$ $\mathbb{R}\backslash \left\{ 1 ight\}$

C. Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)

D. Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)

Hướng dẫn giải:

Tập xác định của hàm số $D = \mathbb{R}\backslash \left\{ 1 ight\}$ $D = \mathbb{R}\backslash \left\{ 1 ight\}$

Ta có: $y' = \frac{3}{{{{\left( { - x + 1} ight)}^2}}} > 0,\forall x e 1$

Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)

Dạng 2: Tìm điều kiện của tham số để hàm số đơn điệu

Điều kiện cần để hàm số đơn điệu:

Giả sử hàm số y = f (x) có đạo hàm trên I. Khi đó:

– Nếu hàm số y = f(x) đồng biến trên I thì f'(x) ≥ 0, ∀ x ∈ I.

– Nếu hàm số y = f(x) nghịch biến trên I thì f'(x) ≤ 0, ∀ x ∈ I.

Điều kiện đủ để hàm số đơn điệu:

– Nếu f'(x) > 0 , ∀ x ∈ I thì hàm số f(x) đồng biến trên I.

– Nếu f'(x) < 0 , ∀ x ∈ I thì hàm số f(x) nghịch biến trên I.

– Nếu f'(x) = 0 , ∀ x ∈ I thì hàm số f(x) không đỏi trên khoảng I.

Phương pháp giải:

Hàm số y = ax³ + bx² + cx + d.

Tập xác định: D= R

y’ = 3ax² + 2bx + c

– Để hàm số đồng biến trên R thì y’ ≥ 0, ∀ x ∈ R.

Khi đó: a > 0; Δ ≤ 0.

– Để hàm số nghịch biến trên R thì y’ ≤ 0, ∀ x ∈ R.

Khi đó: a <0; Δ ≤ 0

Hàm số $y = \frac{{ax + b}}{{cx + d}}$ $y = \frac{{ax + b}}{{cx + d}}$

Tập xác định $D = r\backslash \left\{ {\frac{{ - d}}{c}} \right\};y$ $D = r\backslash \left\{ {\frac{{ - d}}{c}} \right\};y' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}$

Hàm số đồng biến trên các khoảng xác định khi và chỉ khi:

y’ >0, ∀ x ∈ D ⇒ ad-bc > 0

Hàm số nghịch biến trên các khoảng xác định khi và chỉ khi.

y’ < 0, ∀ x ∈ D ⇒ ad-bc < 0.

Ví dụ: Cho hàm số y = mx³ + x + 1.

Tập xác định d = R.

y’ = 3mx² +1.

Để hàm số đồng biến trên R thì:

y’≥ 0, ∀ x ∈ R ⇔ 3mx² +1 ≥ 0; ∀ x ∈ R.

⇔ 3m > 0; Δ= -12m ≤ 0 ⇔ m > 0.

Hàm số nghịch biến trên R thì:

y’ ≤ 0, ∀ x ∈ R ⇔ 3mx² +1 ≤ 0; ∀ x ∈ R.

Khi đó a <0; Δ ≤ 0 ⇔ 3m < 0; -12m ≤ 0 ⇔ m ∈ Ø.

Ví dụ: Số dân số của một thị trấn sau $t$ năm kể từ năm 1970 được ước tính bởi công thức $f(t) = \frac{26t + 10}{t + 5}$ $f(t) = \frac{26t + 10}{t + 5}$ ($f(t)$ được tính bằng nghìn người). Biết rằng đạo hàm của hàm số $f(t)$ biểu thị tốc độ gia tăng dân số của thị trấn ( đơn vị là nghìn người/ năm). Vào năm nào thì tốc độ gia tăng dân số là $\frac{2}{15}$ $\frac{2}{15}$ nghìn người/ năm?

Hướng dẫn giải:

Ta có $f'(t) = \frac{{120}}{{{{\left( {t + 5} ight)}^2}}},t \geqslant 0$

Lại có

$f'(t) = \frac{2}{{15}} \Leftrightarrow \frac{{120}}{{{{\left( {t + 5} ight)}^2}}} = \frac{2}{{15}}$

$\Leftrightarrow (t + 5)^{2} = 900 \Leftrightarrow t = 25\ do\ t \geq 0)$ $\Leftrightarrow (t + 5)^{2} = 900 \Leftrightarrow t = 25\ do\ t \geq 0)$

Vậy dự báo vào năm 1995 thì tốc độ gia tăng dân số là $\frac{2}{15}$ $\frac{2}{15}$ nghìn người/ năm.

Ví dụ: Cho hàm số $y = - x^{3} - mx^{2} + (4m + 9)x + 5$ $y = - x^{3} - mx^{2} + (4m + 9)x + 5$. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số đã cho đồng biến trên $\mathbb{R}$ $\mathbb{R}$?

Hướng dẫn giải:

Ta có: $y' = - 3x^{2} - 2mx + 4m + 9$

Hàm số đã cho nghịch biến trên $\mathbb{R}$ $\mathbb{R}$ khi và chỉ khi $\left\{ \begin{matrix} a < 0 \\ \Delta$ $\left\{ \begin{matrix} a < 0 \\ \Delta' \leq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} - 1 < 0 \\ m^{2} + 3(4m + 9) \leq 0 \\ \end{matrix} ight.$

$\Leftrightarrow m^{2} + 12m + 27 \leq 0 \Leftrightarrow m \in \lbrack - 9; - 3brack$ $\Leftrightarrow m^{2} + 12m + 27 \leq 0 \Leftrightarrow m \in \lbrack - 9; - 3brack$

Mà $m\mathbb{\in Z \Rightarrow}m = \left\{ - 9; - 8;...; - 3 ight\}$ $m\mathbb{\in Z \Rightarrow}m = \left\{ - 9; - 8;...; - 3 ight\}$

Vậy có tất cả 7 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

Ví dụ: Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \frac{x - m}{x + 1}$ $y = \frac{x - m}{x + 1}$ đồng biến trên từng khoảng xác định?

Hướng dẫn giải:

Tập xác định $D\mathbb{= R}\backslash\left\{ - 1 ight\}$ $D\mathbb{= R}\backslash\left\{ - 1 ight\}$

Ta có: $y' = \frac{m + 1}{(x + 1)^{2}};\forall x eq - 1$

Hàm số đã cho đồng biến trên từng khoảng xác định khi và chỉ khi $y' > 0$

$\Leftrightarrow \frac{m + 1}{(x + 1)^{2}} > 0 \Leftrightarrow m + 1 > 0 \Leftrightarrow m > - 1$ $\Leftrightarrow \frac{m + 1}{(x + 1)^{2}} > 0 \Leftrightarrow m + 1 > 0 \Leftrightarrow m > - 1$

Vậy đáp án cần tìm là $m > - 1$.

C. Bài tập tự rèn luyện xét tính đơn điệu của hàm số

Câu 1: Hàm số $y = - x^{3} + 3x^{2} - 4$ $y = - x^{3} + 3x^{2} - 4$ đồng biến trên tập hợp nào trong các tập hợp được cho dưới đây?

A. $(2\ ;\ + \infty)$ $(2\ ;\ + \infty)$ B. $(0\ ;\ 2)$ $(0\ ;\ 2)$ C. $( - \infty\ ;\ 0) \cup (2\ ;\ + \infty)$ $( - \infty\ ;\ 0) \cup (2\ ;\ + \infty)$ D. $( - \infty\ ;\ 0)$ $( - \infty\ ;\ 0)$

Câu 2: Hàm số $y = f(x)$ có đạo hàm $y' = x^{2}$. Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên $\mathbb{R}$ $\mathbb{R}$.

B. Hàm số nghịch biến trên $( - \infty;0)$ $( - \infty;0)$ và đồng biến trên $(0; + \infty)$ $(0; + \infty)$.

C. Hàm số đồng biến trên $\mathbb{R}$ $\mathbb{R}$.

D. Hàm số đồng biến trên $( - \infty;0)$ $( - \infty;0)$ và nghịch biến trên $(0; + \infty)$ $(0; + \infty)$.

Câu 3: Hàm số $y = x^{3} - 3x$ $y = x^{3} - 3x$ nghịch biến trên khoảng nào?

A. $( - \infty; - 1)$ $( - \infty; - 1)$ B. $( - \infty; + \infty)$ $( - \infty; + \infty)$ C. $( - 1;1)$ D. $(0; + \infty)$ $(0; + \infty)$

Câu 4: Cho hàm $y = \sqrt{x^{2} - 6x + 5}$ $y = \sqrt{x^{2} - 6x + 5}$. Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $(5; + \infty).$ $(5; + \infty).$

B. Hàm số đồng biến trên khoảng $(3; + \infty).$ $(3; + \infty).$

C. Hàm số đồng biến trên khoảng $( - \infty;1).$ $( - \infty;1).$

D. Hàm số nghịch biến trên khoảng $( - \infty;3).$ $( - \infty;3).$

Câu 5: Cho hàm số $y = - x^{3} + 3x^{2} - 1$ $y = - x^{3} + 3x^{2} - 1$, kết luận nào sau đây về tính đơn điệu của hàm số là đúng nhất:

A. Hàm số đồng biến trên khoảng $(0;\ 2)$ $(0;\ 2)$ và nghịch biến trên các khoảng $( - \infty;0)$ $( - \infty;0)$; $(2; + \infty)$ $(2; + \infty)$

B. Hàm số đồng biến trên khoảng $(0;2)$;

C. Hàm số nghịch biến trên khoảng $(0;2)$ và đồng biến trên các khoảng $( - \infty;0)$ $( - \infty;0)$; $(2; + \infty)$ $(2; + \infty)$.

D. Hàm số nghịch biến trên các khoảng $( - \infty;0)$ $( - \infty;0)$ và $(2; + \infty)$ $(2; + \infty)$.

Câu 6: Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = x(x - 2)^{3}$, với mọi $x\mathbb{\in R}$ $x\mathbb{\in R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $(1;\ \ 3)$ $(1;\ \ 3)$ B. $( - 1;\ \ 0)$ $( - 1;\ \ 0)$ C. $(0;\ \ 1)$ $(0;\ \ 1)$ D. $( - 2;\ \ 0)$ $( - 2;\ \ 0)$

Câu 7: Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = x + 1$ với mọi $x\mathbb{\in R}$ $x\mathbb{\in R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $( - 1\ ; + \infty)$ $( - 1\ ; + \infty)$ B. $(1\ ; + \infty)$ $(1\ ; + \infty)$ C. $( - \infty\ ; - 1)$ $( - \infty\ ; - 1)$ D. $( - \infty\ ;1)$ $( - \infty\ ;1)$

Câu 8: Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = x + 1$ với mọi $x\mathbb{\in R}$ $x\mathbb{\in R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $( - \infty; - 1)$ $( - \infty; - 1)$ B. $( - \infty;1)$ $( - \infty;1)$ C. $( - 1; + \infty)$ $( - 1; + \infty)$ D. $(1; + \infty)$ $(1; + \infty)$

Câu 9: Hàm số $y = x^{4} - 2x^{2}$ $y = x^{4} - 2x^{2}$ nghịch biến trên khoảng nào dưới đây?

A. $(1\ ;\ + \infty)$ $(1\ ;\ + \infty)$ B. $( - \infty\ ;\ - 1)$ $( - \infty\ ;\ - 1)$ C. $( - 1\ ;\ 0)$ $( - 1\ ;\ 0)$D. $( - \infty\ ;\ 1)$ $( - \infty\ ;\ 1)$

Câu 10: Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = \frac{x + 1}{x + 3m}$ $y = \frac{x + 1}{x + 3m}$ nghịch biến trên khoảng $(6; + \infty)$ $(6; + \infty)$?

A. 0 B. 6 C. 3 D. Vô số

Câu 11: Gọi $S$ là tập hợp tất cả các giá trị của tham số $m$ để hàm số $f(x) = \frac{1}{5}m^{2}x^{5} - \frac{1}{3}mx^{3} + 10x^{2} - \left( m^{2} - m - 20 \right)x$ $f(x) = \frac{1}{5}m^{2}x^{5} - \frac{1}{3}mx^{3} + 10x^{2} - \left( m^{2} - m - 20 \right)x$ đồng biến trên $\mathbb{R}$ $\mathbb{R}$. Tổng giá trị của tất cả các phần tử thuộc $S$ bằng:

A. $\frac{5}{2}$ $\frac{5}{2}$ B. $- 2$ C. $\frac{1}{2}$ $\frac{1}{2}$ D. $\frac{3}{2}$ $\frac{3}{2}$

Câu 12: Tìm tất cả các giá trị thực của tham số để hàm số $y = \frac{\cos\ x - 3}{cos\ x - m}$ $y = \frac{\cos\ x - 3}{cos\ x - m}$ nghịch biến trên khoảng $\left( \frac{\pi}{2};\pi \right)$ $\left( \frac{\pi}{2};\pi \right)$?

A. $\left\lbrack \begin{matrix} 0 \leq m < 3 \\ m \leq - 1 \end{matrix} \right.$ $\left\lbrack \begin{matrix} 0 \leq m < 3 \\ m \leq - 1 \end{matrix} \right.$ B. $\left\lbrack \begin{matrix} 0 < m < 3 \\ m < - 1 \end{matrix} \right.$ $\left\lbrack \begin{matrix} 0 < m < 3 \\ m < - 1 \end{matrix} \right.$ C. $m \leq 3$ $m \leq 3$ D. $m < 3$

Câu 13: Cho hàm số $y = \frac{(4 - m)\sqrt{6 - x} + 3}{\sqrt{6 - x} + m}$ $y = \frac{(4 - m)\sqrt{6 - x} + 3}{\sqrt{6 - x} + m}$. Có bao nhiêu giá trị nguyên của m trong khoảng $( - 10;10)$ sao cho hàm số đồng biến trên $( - 8;5)$?

A. 14 B. 13 C. 12 D. 15

Câu 14: Cho hàm số $y = \frac{\ln x - 4}{\ln x - 2m}$ $y = \frac{\ln x - 4}{\ln x - 2m}$ với $m$ là tham số. Gọi $S$ là tập hợp các giá trị nguyên dương của $m$ để hàm số đồng biến trên khoảng $(1;e)$. Tìm số phần tử của $S$.

A. 3 B. 2 C. 1 D. 4

--------------------------

Tóm lại, Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số là nội dung nền tảng, đóng vai trò quan trọng trong toàn bộ chương trình giải tích lớp 12. Việc thành thạo phần này không chỉ giúp học sinh tự tin khi giải các dạng bài toán khảo sát và vẽ đồ thị mà còn hỗ trợ giải quyết nhanh nhiều dạng toán phức tạp hơn trong đề thi THPT quốc gia môn Toán.

Hy vọng với bản tóm tắt lý thuyết Toán 12 chương 1, học sinh có thể nắm vững kiến thức cốt lõi, đồng thời biết cách áp dụng công thức vào các dạng bài tập điển hình. Để đạt hiệu quả cao, bạn nên kết hợp học lý thuyết song song với luyện tập nhiều dạng bài, đặc biệt là đề minh họa và đề thi chính thức qua các năm. Việc rèn luyện thường xuyên sẽ giúp bạn nâng cao tốc độ, tăng độ chính xác và tự tin chinh phục điểm số cao trong kỳ thi quan trọng.

Tải về

Chọn file muốn tải về: