Trắc nghiệm Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
Chắc chắn rằng việc chuẩn bị tốt cho kỳ thi THPT Quốc gia là ưu tiên hàng đầu của học sinh lớp 12, đặc biệt trong môn Toán. Một trong những chủ đề quan trọng và cần nắm vững trong chương trình Toán 12 là Sự đồng biến, nghịch biến của hàm số. Để giúp các em học sinh ôn tập hiệu quả và hiểu rõ kiến thức, bài viết này sẽ cung cấp một trắc nghiệm Toán 12 chương 1 với các câu hỏi đa dạng, kèm theo đáp án chi tiết, giúp các em tự kiểm tra và củng cố kiến thức về sự đồng biến và nghịch biến của hàm số.
Các câu hỏi trắc nghiệm được thiết kế dựa trên các dạng bài thường gặp trong kỳ thi THPT Quốc gia, giúp học sinh làm quen với cấu trúc đề thi và nâng cao khả năng giải quyết vấn đề một cách nhanh chóng và chính xác. Bài tập này là tài liệu ôn thi hữu ích, hỗ trợ các bạn học sinh hệ thống hóa kiến thức và phát triển kỹ năng làm bài hiệu quả.
Trắc nghiệm Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
Câu 1: Cho đồ thị hàm số với x ∈ [- π/2 ; 3π/2] như hình vẽ.
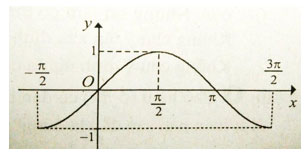
Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- π/2 ; 3π/2]
A. 
\(\left(-\frac{\pi}{2};\frac{\pi}{2}\right)\) B. \(\left(-\frac{\pi}{2};\pi\right)\) C. (-1;1) D. \(\left(0;\pi\right)\)
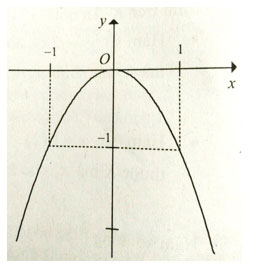
Câu 2: Cho đồ thị hàm số y = -x3 như hình vẽ. Hàm số y = -x3 nghịch biến trên khoảng:
A. (-1;0) B. (-oo;0) C. (0;+oo) D. (-1;1)
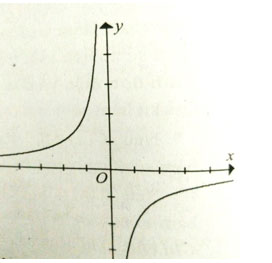
Câu 3: Cho đồ thị hàm số y = -2/x như hình vẽ. Hàm số y = -2/x đồng biến trên
A. (-∞;0) B. (-∞;0) ∪ (0;+∞) C. R D. (-∞;0) và (0;+∞)
Câu 4: Cho hàm số f(x) có đạo hàm f'(x) = √x(x-1)(x+2)2
Kết luận nào sau đây là đúng?
A. Hàm số f(x) nghịch biến trên khoảng (-oo;1).
B. Hàm số f(x) đồng biến trên các khoảng (-oo;0) và (1;+oo).
C. Hàm số f(x) đồng biến trên các khoảng và (1;+oo).
D. Hàm số f(x) đồng biến trên các khoảng (1;+oo).
Câu 5: Khoảng nghịch biến của hàm số y = x3/3 - 2x2 + 3x + 5 là:
A. (1;3) B.(-∞; 1) ∪ (3; +∞) C. (-∞; 1) và (3; +∞) D. (1;+∞)
Câu 6: Cho hàm số y = x4 - 2x2 + 3 . Kết luận nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)
B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)
C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)
D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)
Câu 7: Cho hàm số y = sin2x - 2x. Hàm số này?
A. Luôn đồng biến trên R B. Chỉ đồng biến trên khoảng (0; +∞)
C. Chỉ nghịch biến trên (-∞; -1) D. Luôn nghịch biến trên R
Câu 8: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1)?
A. \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) B. \(y = \frac{{ - 2x + 1}}{{x - 1}}\)
C. \(y = \frac{{x + 1}}{{\sqrt {{x^2} + 1} }}\) D. \(y = \sqrt {x - 1}\)
Câu 9: Tìm m để hàm số \(y = \frac{{ - mx + 2}}{{2x - m}}\) luôn nghịch biến trên khoảng xác định.
A.-2 < m ≤ 2 B. m < -2 hoặc m > 2
C. -2 < m < 2 D. m ≠ ±2
Câu 10: Cho hàm số y = -x3 + 3x2 + 3mx - 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1 B. m ≥ 1 C. m ≤ -1 D. m ≥ -1
Câu 11: Cho đồ thị hàm số có dạng như hình vẽ.
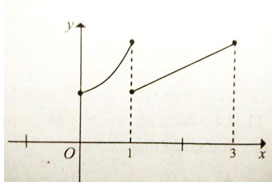
Hàm số đồng biến trên:
A. (0;1) B. (1;3) C. (0; 1) ∪ (1; 3) D. (0;1) và (1;3).
Câu 12: Hỏi hàm số \(y\ =\frac{3x-1}{x+5}\) đồng biến trên các khoảng nào?
A. (-∞ ; +∞) B. (-∞; -5) C. (-5; +∞) ∪ (1; 3) D. (0; 1) và (1; 3)
Câu 13: Tìm khoảng đồng biến của hàm số y = 2x3 - 9x2 + 12x + 3
A.(-∞; 1) ∪ (2; +∞) B. (-∞ 1] và [2; +∞)
C. (-∞; 1) và (2; +∞) D. (1;2)
Câu 14: Khoảng nghịch biến của hàm số y = x4 - 2x2 - 1 là:
A. (-∞; -1) và (0; 1) B. (-∞; 0) và (1; +∞)
C. (-∞; -1) ∪ (0; 1) D. (0;1)
Câu 15: Cho hàm số \(y=\frac{x+1}{x-1}\left(1\right)\). Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số (1) nghịch biến trên R\{1}
B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Câu 16: Tìm khoảng đồng biến của hàm số f(x)= x + cos2x
A. R\{0} B. (-∞; +∞) C. (-1; 1) D. (0; π)
Câu 17: Hàm số: \(y=x-\sqrt{x^2+1}\) đồng biến trên khoảng nào?
A. R B. (-∞; 0) C. (-1; 0) D. (0; +∞)
Câu 18: Cho hàm số y = x3 - x2 + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R?
A. m ≤ 2 B. m > 2 C. m ≥ 2 D. m <2
Câu 19: Cho hàm số \(y=-\frac{x^3}{3}-\frac{mx^2}{2}-2x+1\). Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
A. m < 2√2 B. m ≥ -2√2 C. m = 2√2 D. -2√2 ≤ m 2√2
Câu 20: Tìm tất cả các giá trị của tham số m sao cho hàm số \(y=\frac{\tan x+m}{\tan x+5}\) nghịch biến trên \(\left(-\frac{\pi}{4};\frac{\pi}{4}\right)\)
A. 1 < m < 5 B. m ≥ 5 C. m < -1 hoặc m > 5 D. m > 5
Câu 21. Cho hàm số y = x3 + 3x2 + mx + 1 - 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
A. m =0 B. m = 1/4 C. 9/4 D. Không tồn tại
Câu 22. Cho hàm số \(y = f(x)\) xác định và liên tục trên khoảng \(( - \infty; +
\infty)\), có bảng biến thiên như hình sau:
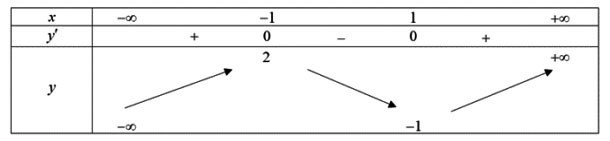Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng \(( -
\infty;1)\).
B. Hàm số đồng biến trên khoảng \(( - 1; +
\infty)\).
C. Hàm số nghịch biến trên khoảng \((1; +
\infty)\).
D. Hàm số đồng biến trên khoảng \(( -
\infty; - 2)\).
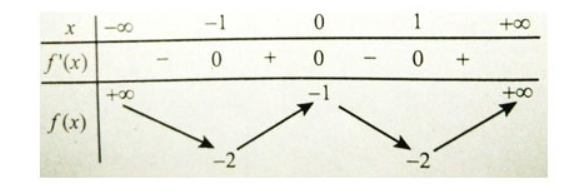
Câu 23. Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
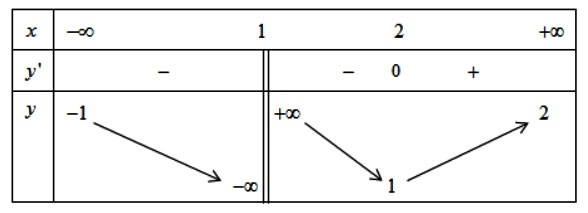
Có bao nhiêu khẳng định sai trong các khẳng định dưới đây?
(i) Đồ thị hàm số có ba đường tiệm cận.
(ii) Hàm số có cực tiểu tại \(x =
2\).
(iii) Hàm số nghịch biến trên mỗi khoảng \(( - \infty; - 1);(1; + \infty)\).
(iv) Hàm số xác định trên \(\mathbb{R}\).
A. 1 B. 2 C. 3 D. 4
Câu 24. Hàm số \(f(x) = \frac{2x + 3}{x -
1}\) nghịch biến trên khoảng nào?
A. \(( - \infty; + \infty)\) B. \(( - \infty;1)\) C. \((1; + \infty)\) D. \(( - \infty;1)\) và \((1; + \infty)\)
Câu 25. Cho hàm số \(y = \frac{2x + 2}{x -
1}\). Khẳng định nào sau đây đúng?
A. Hàm số \(y = f(x)\) nghịch biến trên khoảng \((0; + \infty)\).
B. Hàm số \(y = f(x)\) đồng biến trên khoảng \(( - \infty;2)\).
C. Hàm số \(y = f(x)\) nghịch biến trên khoảng \((2; + \infty)\).
D. Hàm số \(y = f(x)\) đồng biến trên khoảng \((0; + \infty)\).
Hướng dẫn giải và đáp án trắc nghiệm Toán 12 chương 1
| 1-A | 2-C | 3-D | 4-D | 5-A |
| 6-D | 7-D | 8-C | 9-C | 10-C |
| 11-D | 12-D | 13-C | 14-A | 15-B |
| 16-B | 17-A | 18-C | 19-C | 20-D |
| 21-D | 22-D | 23-B | 24-D | 25-C |
Câu 1:
Trên khoảng (-π/2; π/2) đồ thị hàm số đi lên từ trái sang phải.
Trên khoảng (π/2 ; 3π/2) đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số đồng biến trên khoảng (-π/2; π/2)
Chọn đáp án A.
Câu 2:
Trên khoảng (-∞;0) đồ thị hàm số đi lên từ trái sang phải.
Do đó hàm số nghịch biến trên khoảng (0;+∞)
Chọn đáp án C.
Câu 3:
Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)
Chọn đáp án D.
Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:
- Không chú ý tập xác định nên chọn đáp án C.
- Không chú ý định nghĩa của hàm đồng biến nên chọn đáp án B.
Câu 4:
Bảng xét dấu:
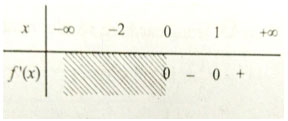
Vậy f(x) đồng biến trên khoảng (1;+∞) và nghịch biến trên khoảng (0;1).
Chọn đáp án D.
Câu 5:
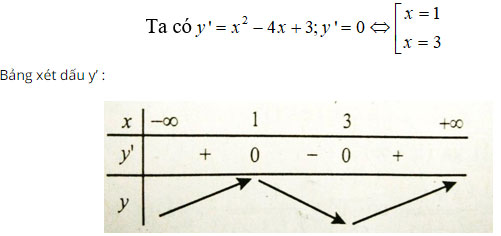
Vậy hàm số nghịch biến trên khoảng (1;3).
Chọn đáp án A.
Câu 6:
Ta có: \(y' = 4{x^3} - 4x \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 1 \hfill \\
x = - 1 \hfill \\
\end{gathered} \right.\)
Bảng xét dấu y':
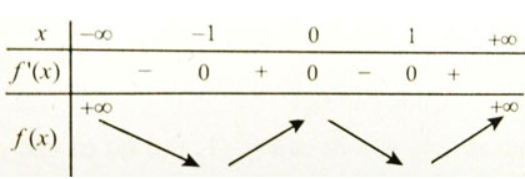
Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞) , nghịch biến trên các khoảng (-∞; -1) và (0; 1) .
Chọn đáp án D.
Câu 7:
Tập xác định D = R Vậy hàm số luôn nghịch biến trên R
Chọn đáp án D.
Câu 8:
Hàm số y = x3/3 - 2x2 + 3x - 1 có y'= x2 - 4x + 3 .
Hàm số đồng biến trên các khoảng (-∞; 1) và (3; +∞) .
Hàm số \(y = \frac{{ - 2x + 1}}{{x - 1}}\) có \(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}};x \ne 1\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right),\left( {1; + \infty } \right)\)
Hàm số \(y = \frac{{x + 1}}{{\sqrt {{x^2} + 1} }}\) có \(y' = \frac{{1 - x}}{{{{\left( {\sqrt {{x^2} + 1} } \right)}^3}}}\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)
Hàm số \(y = \sqrt {x - 1}\)
Hàm số đồng biến trên khoảng (1; +∞) .
Chọn đáp án C.
Câu 9:
Tập xác định \(D=R\left(\frac{m}{2}\right)\)
Hàm số nghịch biến trên từng khoảng (-oo;m/2) và (m/2;+oo)
khi và chỉ khi \(y'=\frac{m^2-4}{\left(2x-m\right)^2}\)< 0 trên D
Suy ra -2 < m < 2.
Chọn đáp án C.
Câu 10:
Ta có y' = -3x2 + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình -3x2 + 6x + 3m. Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1. Hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
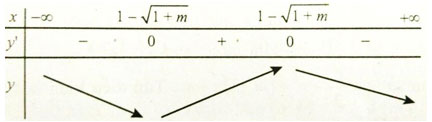
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y' = -3x2 + 6x + 3m ≤ 0, ∀x > 0 <=> 3m ≤ 3x2 - 6x, ∀x > 0
Từ đó suy ra 3m ≤ min(3x2 - 6x) với x > 0 Do đó m ≤ -1.
Chọn đáp án C.
Câu 11:
Trên khoảng (0; 1) đồ thị hàm số đi lên từ trái qua phải
Trên khoảng (1; 3) đồ thị hàm số đi lên từ trái qua phải
Đồ thị hàm số bị gián đoạn tại x = 1. Do đó hàm số đồng biến trên từng khoảng (0; 1) và (1; 3)
Câu 12:
Hàm số xác định ∀x ≠ -5 . Ta có: \(y'=\frac{16}{\left(x+5\right)^2}\)
y' xác định ∀x ≠ -5 . Bảng xét dấu y’:
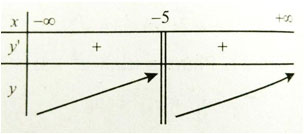
Vậy hàm số đồng biến trên các khoảng (-∞; -5) và (-5; +∞)
Câu 13:
Ta có: \(y'=6x^2-18x+12\) ⇒ \(y'=0;\ x=1,\ x=2\)
Bảng xét dấu đạo hàm:
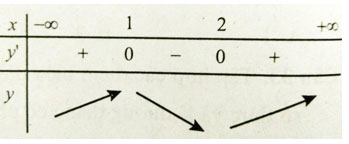
Hàm số đồng biến trên các khoảng (-∞; 1) và (2; +∞)
Câu 14:
Ta có: \(y' = 4{x^3} - 4x \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 1 \hfill \\
x = - 1 \hfill \\
\end{gathered} \right.\)
Bảng xét dấu đạo hàm
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Câu 15:
Hàm số \(y=\frac{x+1}{x-1}\) xác định ∀x ≠ 1
Ta có: \(y'=\ \frac{-2}{\left(x-1\right)^2};\ y'\) xác định ∀x ≠ 1
Bảng xét dấu đạo hàm
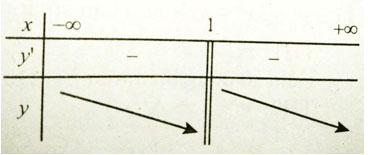
Hàm số nghịch biến trên các khoảng (-∞ 1) và (1; +∞)
Câu 16:
f'(x) = 1 - 2sinxcosx = (sinx - cosx)2 ≥ 0 ∀x ∈ R
Hàm số đồng biến trên khoảng (-∞; +∞)
Câu 17:
Ta có: \(y = 1 - \frac{x}{{\sqrt {{x^2} + 1} }} > 0\); ∀x∈R
Hàm số đồng biến trên R
Câu 18:
y' = x2 - 2x + (m -1). Hàm số đồng biến trên R
<=> y' > 0 ∀x ∈ R <=> Δ' ≥ 0; Δ' = -m + 2 ≥ 0 <=> m > 2
Câu 19:
Ta có y' = -x2 - mx - 2 . Hàm số nghịch biến trên khoảng (-∞; - 1) nếu y' = x2 - mx - 2 ≤ 0 trên khoảng (-∞; -1)
Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có Δ = m2 - 8
TH1: -2√2 ≤ m ≤ 2√2 => Δ ≤ 0. Hàm số nghịch biến trên R
TH2: \(\left[ \begin{gathered}
m < - 2\sqrt 2 \hfill \\
m > 2\sqrt 2 \hfill \\
\end{gathered} \right. \Rightarrow \Delta > 0\)
y' = 0 có hai nghiệm phân biệt là: \(x = \frac{{ - m \pm \sqrt {{m^2} - 8} }}{2}\)
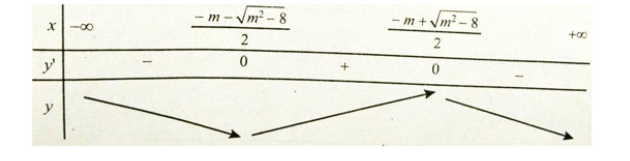
Từ TH1 và TH2, ta có m ≤ 2√2
Cách 2. Dùng phương pháp biến thiên hàm số
Ta có:
\(mx \geqslant - {x^2} - 2;\forall x < - 1\)
\(\Leftrightarrow m \leqslant \frac{{ - {x^2} - 2}}{x};\forall x < - 1\)
Từ đó suy ra: \(\Leftrightarrow m \leqslant \frac{{ - {x^2} - 2}}{x};\forall x < - 1\)
Do đó m ≤ 2√2
Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là m = 2√2
Câu 20:
Ta có:\(y' = \frac{{5 - m}}{{{{\cos }^2}x{{\left( {\tan x + 5} \right)}^2}}} < 0 \Leftrightarrow m > 5\)
Câu 21:
y' = 3x2 + 6x + m. Hàm số đồng biến nếu y' ≥ 0. Ta có Δ' = 9 - 3m
TH1: m ≥ 3 => Δ' ≤ 0 .
Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài
TH2: m < 3 => Δ' > 0 . y’ có hai nghiệm phân biệt là
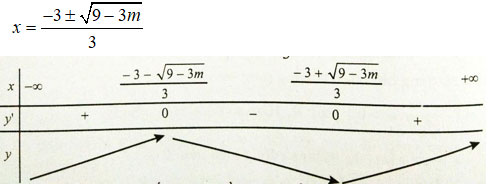
Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.
Câu 22:
Dựa vào bảng biến thiên ta thấy:
Hàm số nghịch biến trên khoảng \(( -
1;1)\)
Hàm số đồng biến trên khoảng \(( - \infty;
- 1) \cup (1; + \infty)\)
Vậy đáp án cần tìm là: “Hàm số đồng biến trên khoảng \(( - \infty; - 2)\)”.
Câu 23:
Do \(\lim_{x \rightarrow - \infty}f(x) = -
1;\lim_{x \rightarrow + \infty}f(x) = 2\) nên đồ thị hàm số có hai đường tiệm cận ngang; \(\lim_{x
\rightarrow 1^{\pm}}f(x) = \pm \infty\) nên đồ thị hàm số có một tiệm cận đứng. Do đó đồ thị hàm số có ba đường tiệm cận nên (i) đúng.
Hàm số có cực tiểu tại \(x = 2\) đúng nên (ii) đúng.
Hàm số nghịch biến trên \(( - \infty; -
1);(1;2)\) nên (iii) sai.
Hàm số không xác định tại \(x = 1\) nên (iv) sai.
Vậy có 2 khẳng định sai.
Câu 24:
Tập xác định \(D\mathbb{=
R}\backslash\left\{ 1 \right\}\)
\(f'(x) = \frac{- 5}{(x - 1)^{2}} <
0;\forall x \in D\) suy ra hàm số nghịch biến trên \(( - \infty;1)\) và \((1; + \infty)\).
Câu 25:
Ta có: \(y' = \frac{- 4}{(x - 1)^{2}}
< 0;\forall x \neq 1\)
Suy ra hàm số nghịch biến trên khoảng \(( -
\infty;1),(1; + \infty)\)
Mà \((2; + \infty) \subset (1; +
\infty)\) nên hàm số cũng nghịch biến trên khoảng \((2; + \infty)\).
--------------------------------------------------------------------------
Hy vọng rằng bộ trắc nghiệm Toán 12 chương 1 về sự đồng biến, nghịch biến của hàm số sẽ là công cụ hữu ích giúp các em ôn luyện và đạt kết quả cao trong kỳ thi THPT Quốc gia. Việc làm quen với các câu hỏi trắc nghiệm, nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp các em tự tin hơn trong ngày thi. Đừng quên tham khảo thêm các bài tập khác trong các chương tiếp theo của chương trình Toán 12 để hoàn thiện kỹ năng và nâng cao điểm số.
Nếu bạn thấy bài viết hữu ích, hãy chia sẻ với bạn bè và học sinh khác để cùng nhau ôn luyện và tiến bộ. Để theo dõi thêm nhiều bài viết và bài tập ôn thi Toán 12, đừng quên truy cập thường xuyên vào trang web của chúng tôi. Chúc các em học sinh ôn thi hiệu quả và đạt kết quả như mong muốn trong kỳ thi THPT Quốc gia sắp tới!
