Khoảng cách giữa 2 đường thẳng trong không gian Oxyz
Toán 12: Khoảng cách giữa 2 đường thẳng trong không gian Oxyz
Trong chương trình Toán học lớp 12, đặc biệt khi ôn thi THPT Quốc gia, chuyên đề hình học không gian luôn chiếm một vị trí quan trọng. Một trong những kiến thức trọng tâm mà học sinh cần nắm vững là khoảng cách giữa hai đường thẳng trong không gian Oxyz. Bài viết dưới đây sẽ giúp bạn hệ thống lại lý thuyết, công thức tính và phương pháp giải nhanh các dạng bài thường gặp, từ đó tự tin chinh phục điểm số cao trong kỳ thi sắp tới.
KHOẢNG CÁCH GIỮA 2 ĐƯỜNG THẲNG TRONG KHÔNG GIAN
Trong không gian hai đường thẳng có 4 vị trí tương đối là: Trùng nhau; Cắt nhau; Song song; Chéo nhau.
Trường hợp hai đường thẳng trùng nhau hay cắt nhau thì ta có thể coi khoảng cách giữa chúng bằng 0.
Nếu hai đường thẳng song song thì khoảng cách giữa chúng là khoảng cách từ điểm bất kỳ trên đường thẳng này đến đường thẳng kia.
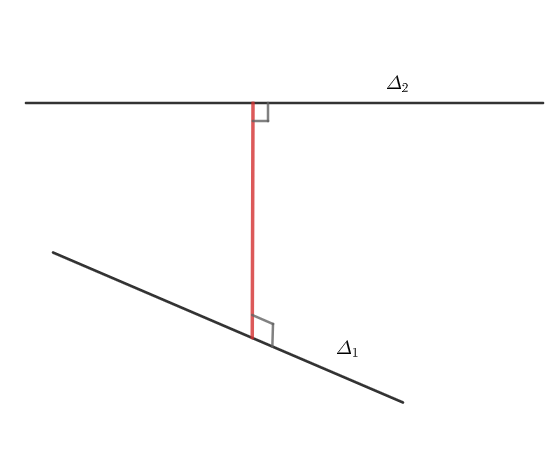
Còn trong trường hợp hai đường thẳng chéo nhau thì khoảng cách giữa chúng là độ dài đoạn vuông góc chung. Trong đó đoạn vuông góc chung là đoạn thẳng nối hai điểm trên hai đường thẳng chéo nhau đồng thời vuông góc với cả hai đường thẳng đó. Đoạn vuông góc chung của hai đường thẳng chéo nhau là tồn tại và duy nhất.
TÍNH KHOẢNG CÁCH GIỮA 2 ĐƯỜNG THẲNG TRONG KHÔNG GIAN OXYZ
1. Khoảng cách giữa 2 đường thẳng song song trong Oxyz
Trong không gian Oxyz, giả sử cho 2 đường thẳng song song có phương trình:
\({\Delta _1}:\left\{ \begin{gathered}
x = {x_1} + a{t_1} \hfill \\
y = {y_1} + b{t_1} \hfill \\
z = {z_1} + c{t_1} \hfill \\
\end{gathered} \right.;\left( {{t_1} \in \mathbb{R}} \right)\) và \({\Delta _2}:\left\{ \begin{gathered}
x = {x_2} + a{t_2} \hfill \\
y = {y_2} + b{t_2} \hfill \\
z = {z_2} + c{t_2} \hfill \\
\end{gathered} \right.;\left( {{t_2} \in \mathbb{R}} \right)\)
Để tính khoảng cách giữa hai đường thẳng trên ta sử dụng công thức:
\(d\left( {{\Delta _1};{\Delta _2}} \right) = \frac{{\left| {\overrightarrow {{M_1}{M_2}} \wedge \overrightarrow u } \right|}}{{\left| {\overrightarrow u } \right|}}\)
Trong đó \({{M_1}{M_2}}\) là điểm bất kỳ lần lượt trên hai đường thẳng \({{\Delta _1};{\Delta _2}}\)
Để thuận tiện ta thường lấy \({M_1} = \left( {{x_1};{y_1};{z_1}} \right)\) và \({M_2} = \left( {{x_2};{y_2};{z_2}} \right)\)
Còn \({\overrightarrow u }\) là một vectơ chỉ phương bất kì của một trong hai đường thẳng \({{\Delta _1};{\Delta _2}}\) .
Ta thường lấy \(\overrightarrow u = \left( {a;b;c} \right)\)
Ví dụ minh họa: Trong không gian Oxyz cho hai đường thẳng có phương trình lần lượt là
\({\Delta _1}:\left\{ \begin{gathered}
x = 1 + 2{t_1} \hfill \\
y = 2 + 2{t_1} \hfill \\
z = 3 - 3{t_1} \hfill \\
\end{gathered} \right.;\left( {{t_1} \in \mathbb{R}} \right)\) và \({\Delta _2}:\left\{ \begin{gathered}
x = 3 + 4{t_2} \hfill \\
y = 2 + 4{t_2} \hfill \\
z = 5 - 6{t_2} \hfill \\
\end{gathered} \right.;\left( {{t_2} \in \mathbb{R}} \right)\)
Tính khoảng cách giữa hai đường thẳng đó.
Hướng dẫn giải
Lưu ý: Nhìn vào hệ số của tham số ở hai phương trình ta dễ nhận thấy hai đường thẳng song song hoặc trùng nhau. Chúng ta sẽ không kiểm tra nó song song hay trùng nhau mà áp dụng ngay công thức tính khoảng cách bên trên. Nếu ra kết quả bằng 0 thì hai đường thẳng trùng nhau. Nếu ra kết quả khác 0 thì hai đường thẳng đó song song.
Ta có: \({M_1} = \left( {1;2;3} \right)\), \({M_2} = \left( {3;2;5} \right)\) suy ra \(\overrightarrow {{M_1}{M_2}} = \left( {2;0;2} \right)\)
\(\overrightarrow u = \left( {2;2; - 3} \right)\) là một vectơ chỉ phương của hai đường thẳng \({{\Delta _1};{\Delta _2}}\)
Khi đó khoảng cách giữa hai đường thẳng \({{\Delta _1};{\Delta _2}}\) là:
\(d\left( {{\Delta _1};{\Delta _2}} \right) = \frac{{\left| {\overrightarrow {{M_1}{M_2}} \wedge \overrightarrow u } \right|}}{{\left| {\overrightarrow u } \right|}} = \frac{{2\sqrt {561} }}{{17}}\)
2. Khoảng cách giữa 2 đường thẳng chéo nhau trong Oxyz
Trong không gian Oxyz, giả sử cho 2 đường thẳng chéo nhau có phương trình:
\({\Delta _1}:\left\{ \begin{gathered}
x = {x_1} + a{t_1} \hfill \\
y = {y_1} + b{t_1} \hfill \\
z = {z_1} + c{t_1} \hfill \\
\end{gathered} \right.;\left( {{t_1} \in \mathbb{R}} \right)\) và \({\Delta _2}:\left\{ \begin{gathered}
x = {x_2} + a{t_2} \hfill \\
y = {y_2} + b{t_2} \hfill \\
z = {z_2} + c{t_2} \hfill \\
\end{gathered} \right.;\left( {{t_2} \in \mathbb{R}} \right)\)
Để tính khoảng cách giữa hai đường thẳng trên ta sử dụng công thức:
\(d\left( {{\Delta _1};{\Delta _2}} \right) = \frac{{\left| {\left( {{{\overrightarrow u }_1} \wedge \overrightarrow {{u_2}} } \right)\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {{{\overrightarrow u }_1} \wedge \overrightarrow {{u_2}} } \right|}}\)
Trong đó \({{M_1}{M_2}}\) là điểm bất kỳ lần lượt trên hai đường thẳng \({{\Delta _1};{\Delta _2}}\)
Để thuận tiện ta thường lấy \({M_1} = \left( {{x_1};{y_1};{z_1}} \right)\) và \({M_2} = \left( {{x_2};{y_2};{z_2}} \right)\)
Còn \({\overrightarrow u _1};\overrightarrow {{u_2}}\) lần lượt là một vectơ chỉ phương bất kì của một trong hai đường thẳng \({{\Delta _1};{\Delta _2}}\) .
Ta thường lấy \({\overrightarrow u _1} = \left( {{a_1};{b_1};{c_1}} \right)\) và \(\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\)
Ví dụ minh họa: Trong không gian Oxyz cho hai đường thẳng có phương trình lần lượt là
\({\Delta _1}:\left\{ \begin{gathered}
x = 1 + 2{t_1} \hfill \\
y = 2 + 2{t_1} \hfill \\
z = 1 - 1{t_1} \hfill \\
\end{gathered} \right.;\left( {{t_1} \in \mathbb{R}} \right)\) và \({\Delta _2}:\left\{ \begin{gathered}
x = 1 + 2{t_2} \hfill \\
y = 2 + 2{t_2} \hfill \\
z = 1 - 1{t_2} \hfill \\
\end{gathered} \right.;\left( {{t_2} \in \mathbb{R}} \right)\)
Tính khoảng cách giữa hai đường thẳng đó.
Hướng dẫn giải
Lưu ý: Trong công thức tính khoảng cách 2 đường thẳng chéo nhau ở trên. Nếu chúng ta áp dụng cho 2 đường thẳng song song hoặc trùng nhau thì mẫu số sẽ bằng 0 và phép tính không tính được. Còn nếu áp dụng cho hai đường thẳng cắt nhau ta được kết quả bằng 0. Áp dụng cho hai đường thẳng chéo nhau thì kết quả khác 0. Vì vậy khi làm bài ta sẽ nhận xét nhanh hai đường thẳng có rơi vào trường hợp song song hay trùng nhau không. Sau đó ta áp dụng công thức.
Ta có: \({M_1} = \left( {1;2;1} \right)\), \({M_2} = \left( {1;3;2} \right)\) suy ra \(\overrightarrow {{M_1}{M_2}} = \left( {0;1;1} \right)\)
\(\overrightarrow u_1 = \left( {2;2; - 1} \right)\) là một vectơ chỉ phương của hai đường thẳng \({{\Delta _1}}\)
\(\overrightarrow u_2 = \left( {2;-1; - 2} \right)\) là một vectơ chỉ phương của hai đường thẳng \({\Delta _2}\)
Khi đó khoảng cách giữa hai đường thẳng \({{\Delta _1};{\Delta _2}}\) là:
\(d\left( {{\Delta _1};{\Delta _2}} \right) = \frac{{\left| {\left( {{{\overrightarrow u }_1} \wedge \overrightarrow {{u_2}} } \right)\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {{{\overrightarrow u }_1} \wedge \overrightarrow {{u_2}} } \right|}} = \frac{{4\sqrt {65} }}{{65}}\)
3. Bài tập minh họa có hướng dẫn chi tiết tính khoảng cách trong không gian
Bài 1: Để tính khoảng cách từ điểm \(M\left( x_{1},y_{1},z_{1} \right)\) đến đường thẳng \((D):\frac{x - x_{0}}{a_{1}} =
\frac{y - y_{0}}{a_{2}} = \frac{z - z_{0}}{a_{3}}\ \ \left( a_{1},\
a_{2},\ a_{3} \neq \ 0 \right)\), một học sinh lý luận qua các giai đoạn sau:
I. Vẽ MH vuông góc với (D) tại H. Ta có: \(A\left( x_{0},\ y_{0},\ z_{0} \right) \in
(D);\) vectơ chỉ phương của (D) là: \(\overrightarrow{a} = \left( a_{1},\ a_{2},\ a_{3}
\right).\)
\(\overrightarrow{AM} = \left(
b_{1},b_{2},b_{3} \right) = \left( x_{1} - x_{0},y_{1} - y_{0};z_{1} -
z_{0} \right)\)
II. \(\overrightarrow{AH}\) cùng phương với \(\overrightarrow{a}\), ta có: \(\overrightarrow{AH} =
k\overrightarrow{a}\)
Diện tích tam giác AMH: \(S =
\frac{1}{2}AH.MH = \frac{|k|.\left| \overrightarrow{a}
\right|.MH}{2}\) \((1)\)
III. Dùng tích hữu hướng, ta có diện tính tam giác AMH:
\(S = \frac{1}{2}\left| \left\lbrack
\overrightarrow{AH},\overrightarrow{AM} \right\rbrack \right| =
\frac{|k|}{2}.\left| \left\lbrack \overrightarrow{a},\overrightarrow{AM}
\right\rbrack \right|\) \((2)\)
Từ \((1)\) và \((2)\), ta có: \(\left| \overrightarrow{a} \right|.MH = \left|
\left\lbrack \overrightarrow{a},\overrightarrow{AM} \right\rbrack
\right|\)
Vậy \(d(M,D) = \frac{\left| \left\lbrack
\overrightarrow{a},\overrightarrow{AM} \right\rbrack \right|}{\left|
\overrightarrow{a} \right|}\)
Lý luận trên đúng hay sai, nếu sai thì sai ở đoạn nào?
A. Chỉ I B. Chỉ II C. Chỉ III D. Chỉ II và III
Hướng dẫn giải
Sai ở giai đoạn II, vì \(\overrightarrow{AH} = k\overrightarrow{a}\) thì\(k \in R\backslash\left\{ 0
\right\}\)
Chọn đáp án C
Bài 2: Cho hai đường thẳng chéo nhau \(\left( D_{1} \right):\ \frac{x\ - \ x_{1}}{a_{1}}
= \frac{y\ - \ y_{1}}{a_{2}} = \frac{z\ - \ z_{1}}{a_{3}}\) và \(\left( D_{2} \right):\ \frac{x\ - \
x_{2}}{b_{1}} = \frac{y\ - \ y_{2}}{b_{2}} = \frac{z\ - \
z_{2}}{b_{3}}\) \(\left(
a_{1},a_{2},a_{3},b_{1},b_{2},b_{3} \neq \ \ 0 \right);\) với \(\overrightarrow{a} = \left(
a_{1},a_{2},a_{3} \right)\); \(\overrightarrow{b} = \left( b_{1},b_{2},b_{3}
\right)\) và \(\overrightarrow{AB} =
\left( x_{2} - x_{1},y_{2} - y_{1},z_{2} - z_{1} \right).\) Khoảng cách hay đoạn vuông góc chung giữa \(\left( D_{1} \right)\) và \(\left( D_{2} \right)\) tính bởi công thức nào sau đây?
A. \(d\left( D_{1},D_{2} \right) =
\frac{\left| \left\lbrack
\overrightarrow{a},\overrightarrow{b},\overrightarrow{AB} \right\rbrack
\right|}{\left| \left\lbrack \overrightarrow{a},\overrightarrow{b}
\right\rbrack \right|}\) B. \(d\left(
D_{1},D_{2} \right) = \frac{\left| \left\lbrack
\overrightarrow{a},\overrightarrow{b} \right\rbrack \right|}{\left|
\left\lbrack \overrightarrow{a},\overrightarrow{b},\overrightarrow{AB}
\right\rbrack \right|}\)
C. \(d\left( D_{1},D_{2} \right) =
\frac{\left| \left\lbrack \overrightarrow{a},\overrightarrow{b}
\right\rbrack.\overrightarrow{AB} \right|}{\left| \left\lbrack
\overrightarrow{a},\overrightarrow{b} \right\rbrack \right|}\) D. \(d\left( D_{1},D_{2} \right) = \frac{\left|
\left\lbrack \overrightarrow{a},\overrightarrow{b}.\overrightarrow{AB}
\right\rbrack \right|}{\left| \left\lbrack
\overrightarrow{a},\overrightarrow{b} \right\rbrack
\right|}\)
Hướng dẫn giải
Công thức đúng là: \(d\left( D_{1},D_{2}
\right) = \frac{\left| \left\lbrack
\overrightarrow{a},\overrightarrow{b} \right\rbrack.\overrightarrow{AB}
\right|}{\left| \left\lbrack \overrightarrow{a},\overrightarrow{b}
\right\rbrack \right|}\)
Chọn đáp án C
Bài 3: Cho ba điểm \(A( -
4,4,0),B(2,0,4),C(1,2, - 1)\) .Khoảng cách từ C đến đường thẳng AB bằng bao nhiêu?
Hướng dẫn giải
Ta có:
\(\overrightarrow{CA} = ( - 5,2,1)\) ;\(\overrightarrow{CB} = (1, - 2,5)\) ;\(\overrightarrow{AB} = (6, - 4,4)\) .
Khoảng cách cần tìm bằng: \(\frac{\left|
\left\lbrack \overrightarrow{CA},\overrightarrow{CB} \right\rbrack
\right|}{\overrightarrow{AB}} = \frac{2\sqrt{36 + 169 + 16}}{2\sqrt{9 +
4 + 4}} = \sqrt{13}.\)
Vậy chọn A.
Bài 4: Cho hình hộp chữ nhật \(ABCD.EFGH\) có \(AB = a;\ \ AD = b;\ \ AE = c\) trong hệ trục \(Oxyz\) sao cho \(A\) trùng với \(O;\ \
\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE}\) lần lượt trùng với \(Ox,Oy,Oz\). Gọi \(M,N,P\) lần lượt là trung điểm \(BC,EF,DH\). Tính khoảng cách giữa \(NP\) và \(CG\).
A. \(\frac{2ab\sqrt{a^{2} + 4b^{2}}}{a^{2}
+ 4b^{2}}\) B. \(abc\) C. \(\frac{\sqrt{a^{2} + 4b^{2}}}{2ab}\) D. \(\frac{c}{a}\sqrt{a^{2} +
4b^{2}}\)
Hướng dẫn giải
Ta có:
\(N\left( \frac{a}{2},0,c \right);P\left(
0,b,\frac{c}{2} \right);C(a,b,0);G(a,b,c)\)
\(= > \overrightarrow{NP} = \left( -
\frac{a}{2},b, - \frac{c}{2} \right);\overrightarrow{CG} =
(0,0,c);\overrightarrow{PC} = \left( a,0, - \frac{c}{2}
\right)\)
\(= > \left\lbrack
\overrightarrow{CG},\overrightarrow{NP} \right\rbrack = \left( - bc, -
\frac{ac}{2},0 \right) = > \left| \left\lbrack
\overrightarrow{CG},\overrightarrow{NP} \right\rbrack \right| =
\frac{c}{2}\sqrt{a^{2} + 4b^{2}}\)
\(\left\lbrack\overrightarrow{CG},\overrightarrow{NP}\right\rbrack.\overrightarrow{PC} = - abc\)
Vậy khoảng cách giữa hai đường thẳng NP và CG là:
\(d(NP,CG) =\frac{2ab\sqrt{a^{2} + 4b^{2}}}{a^{2} + 4b^{2}}\).
4. Bài tập tự rèn luyện tính khoảng cách giữa hai đường thẳng trong không gian Oxyz
Bài 1. Trong không gian \(Oxyz\),cho hai đường thẳng \(d:\left\{ \begin{matrix}
x = 1 - t \\
y = t \\
z = - t \\
\end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)\) và \(d':\left\{ \begin{matrix}
x = 2t' \\
y = - 1 + t' \\
z = t' \\
\end{matrix} \right.\ ;\left( t'\mathbb{\in R} \right)\). Khoảng cách giữa hai đường thẳng \(d\) và \(d'\) bằng bao nhiêu?
Bài 2. Trong không gian với hệ tọa độ \(Oxyz\), tính khoảng cách giữa đường thẳng \(d:\frac{x - 1}{2} = \frac{y + 2}{- 4} =
\frac{z - 4}{3}\) và trục \(Ox\).
Bài 3. Trong không gian \(Oxyz\), cho hai đường thẳng \(d_{1}:\frac{x - 1}{2} =
\frac{y}{1} = \frac{z}{3},d_{2}:\left\{ \begin{matrix}
x = 1 + t \\
y = 2 + t \\
z = m \\
\end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)\). Gọi \(S\) là tập hợp tất cả các số \(m\) sao cho \(d_{1},d_{2}\) chéo nhau và khoảng cách giữa chúng bằng \(\frac{5}{\sqrt{19}}\). Tính tổng tất cả các phần tử của \(S\).
--------------------------------------------------------------
Việc thành thạo cách tính khoảng cách giữa hai đường thẳng trong không gian Oxyz không chỉ giúp bạn giải nhanh các bài toán trong đề thi THPT Quốc gia mà còn rèn luyện tư duy hình học không gian sắc bén. Hãy luyện tập thật nhiều, kết hợp ghi nhớ công thức và phương pháp suy luận để làm chủ chuyên đề này. Nếu bạn cần thêm tài liệu ôn luyện, đề thi thử hoặc bài giảng chi tiết các chuyên đề Hình học không gian 12. Đây là nội dung thường xuất hiện trong các bài kiểm tra môn Toán lớp 12, cũng như bài thi THPT Quốc gia môn Toán, vì vậy các em học sinh cần ôn tập kỹ phần kiến thức này để có thể đạt điểm cao trong các bài thi của mình. Đừng ngần ngại theo dõi các bài viết tiếp theo trên VnDoc.com hoặc truy cập chuyên mục Ôn thi THPT Quốc gia môn Toán để cập nhật kiến thức mới nhất. Chúc các bạn học tốt và đạt kết quả cao trong kỳ thi sắp tới!
