Trắc nghiệm Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số

Trắc nghiệm Toán 12 chương 1 có lời giải

Khảo sát sự biến thiên và vẽ đồ thị hàm số

Để giúp các bạn học sinh lớp 12 học tập hiệu quả hơn môn Toán, VnDoc.com đã tổng hợp bộ câu hỏi trắc nghiệm kèm theo đáp án và lời giải chi tiết sẽ giúp các bạn học sinh giải bài tập Toán 12 một cách dễ dàng. Mời các bạn học sinh và thầy cô tham khảo.

VnDoc.com xin gửi tới bạn đọc bài viết Trắc nghiệm Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số để bạn đọc cùng tham khảo. Bài viết gồm có 19 bài tập về việc khảo sát sự biến thiên và vẽ đồ thị hàm số. Bài tập có đáp án kèm theo. Mời các bạn cùng tham khảo chi tiết và tải về tại đây.

Trắc nghiệm Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số

Câu 1: Đường cong trong hình dưới đây là đồ thị của một hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

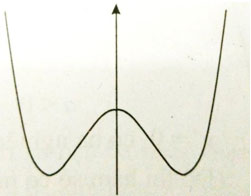
Khảo sát sự biến thiên và vẽ đồ thị hàm số

A. y = x⁴ + 3x² - 2

B. y = x³ - 2x² + 1

C. y = -4x⁴ + x² + 4

D. y = x⁴ - 2x² + 3

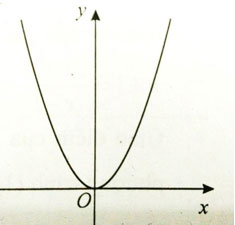
Câu 2: Đồ thị trong hình dưới đây là đồ thị của đồ thị hàm số nào?

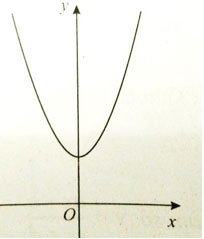
A. y = x² - 2x + 1

B. y = x³ + 4x² - 2x + 5

C. y = x⁴ + x² + 1

D. y = x⁴ - 3x² + 5

Câu 3: Tâm đối xứng của đồ thị hàm số y = -x³ - 3x² + 1 là?

A. (-1; -1)

B. (-2; -3)

C. (0; 1)

D. Không có đáp án

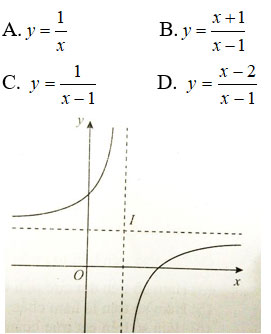
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?

A. I(1; 0) là tâm đối xứng của $y\ =\ \frac{x+1}{x-1}$ $y\ =\ \frac{x+1}{x-1}$

B. I(1; 0) là tâm đối xứng của y = -x³ + 3x² - 2

C. I(1; 0) là điểm thuộc đồ thị $y=\frac{x+1}{x-1}$ $y=\frac{x+1}{x-1}$

D. I(1; 0) là giao điểm của y = x³ - 3x² - 2 với trục hoành.

Câu 5: Tìm m để bất phương trình x⁴ + 2x² ≥ m luôn đúng.

A. m = 0

B. m < 0

C. m ≤ 0

D. Không có đáp án

Câu 6: Cho hàm số $y\ =\frac{1}{3}x^3+x^2-2$ $y\ =\frac{1}{3}x^3+x^2-2$. Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là?

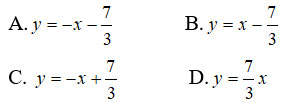
Câu 7: Cho hàm số $y\ =\ \frac{1}{3}x^3-2x^2+3x+1\ \left(c\right)$ $y\ =\ \frac{1}{3}x^3-2x^2+3x+1\ \left(c\right)$. Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x -1

A. y = 3x + 1

B. y = 3x - 29/3

C. 3x + 20

D. Cả A và B đúng

Câu 8: Gọi M, N là giao điểm của $y\ =\ x+1$ $y\ =\ x+1$ và $y\ =\ \frac{2x+4}{x-1}$ $y\ =\ \frac{2x+4}{x-1}$ . Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng

A. 2

B.1

C. 0

D. -1

Câu 9: Tìm m để phương trình x³ + 3x² = m có ba nghiệm phân biệt

A. m > 4

B. m < 0

C. 0 ≤ m ≤ 4

D. 0 < m < 4

Câu 10: Cho hàm số 2x³ - 3(m+1)x² + 6(m + 1)2x + 1. Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?

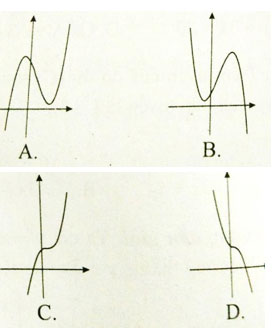
Câu 11: Cho hàm số y = x⁴ + (m² + 1)x² + 1. Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?

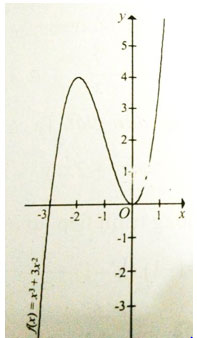
Câu 12: Cho đồ thị hàm số f(x) như hình bên. Hàm số nào dưới đây tương ứng với đồ thị đó?

Câu 13: Đồ thị hàm số y = x³ - 3x cắt

A. Đường thẳng y = 3 tại hai điểm.

B. Đường thẳng y = -4 tại hai điểm.

C. Đường thẳng y = 5/3 tại ba điểm.

D. Trục hoành tại một điểm.

Câu 14: Đường thẳng y = 3x + m là tiếp tuyến của đường cong y = x³ + 2 khi m bằng?

A. 1 hoặc -1

B. 3 hoặc -3

C. 4 hoặc 0

D. 2 hoặc -2

Câu 15: Tiếp tuyến của parabol y = 4 - x² tại điểm (1; 3) tạo với hai trục tọa độ một tam giác vuông. Diện tích tam giác vuông đó là?

A. 25/2

B. 25/4

C. 5/2

D. 5/4

Câu 16: Cho hàm số y = 3x - 4x³. Có nhiều nhất mấy tiếp tuyến với đồ thị hàm số đi qua điểm M(1; 3)?

A. 1

B. 2

C. 3

D.4

Câu 17: Tìm m để phương trình x⁴ - 2x² + 3 - m² + 2m = 0 có đúng ba nghiệm phân biệt

A. m = -1

B. m = 3

C. -1 < m < 3

D. Cả A và B

Câu 18: Với m > 0 phương trình

có ít nhất mấy nghiệm?

A. 0

B. 1

C. 2

D.3

Câu 19: Với mọi m ∈ (-1; 1) phương trình sin² + cosx = m có mấy nghiệm trên đoạn [0; π]?

A. 0

B. 1

C. 2

D.3

Hướng dẫn giải và đáp án trắc nghiệm Toán 12 chương 1

1-D	2-C	3-A	4-B	5-C
6-A	7-D	8 - B	9 - D	10-C
11-C	12-D	13-C	14-C	15-B
16-B	17-D	18-A	19-C

Câu 1:

Theo Chú ý ở mục 2, đồ thị ứng với hàm bậc bốn trùng phương có a > 0 và a, b, trái dấu.

Chọn đáp án D.

Câu 2:

Theo Chú ý ở mục 2, đồ thị ứng với hàm bậc bốn trùng phương có a > 0 và a, b, cùng dấu hoặc hàm số bậc hai với a > 0. Tuy nhiên đỉnh của parabol của đồ thị hàm số y = -x³ - 3x² + 1 là I(1; 0) nằm trên trục hoành.

Chọn đáp án C.

Câu 3:

y' = -3x² - 6x; y'' = -6x - 6; y'' = 0 => x = -1

Vậy điểm U(-1; -1) là tâm đối xứng của đồ thị (theo chú ý ở mục 1).

Chọn đáp án A.

Câu 4:

A. Tâm đối xứng của $y=\ \frac{x+1}{x-1}$ $y=\ \frac{x+1}{x-1}$ là E (1;1)

C. Điểm I(1; 0) không thuộc đồ thị $y\ =\ \frac{x+1}{x-1}$ $y\ =\ \frac{x+1}{x-1}$

D. Điểm I(1; 0) không thuộc đồ thị y = x³ - 3x² - 2 nên không phải là giao điểm của y = x³ - 3x²- 2 với trục hoành.

Chọn đáp án B.

Câu 5:

Xét hàm y = x⁴ + 2x² ≤ m có a = 1 > 0; b = 2 > 0 => a, b cùng dấu.

Đồ thị có dạng như hình bên.

Từ đồ thị hàm số ta suy ra m ≤ 0 .

Chọn đáp án C.

Khảo sát sự biến thiên và vẽ đồ thị hàm số

Câu 6:

Ta có

y' = x² + 2x; y'' = 2x + 2 => y'' = 0 <=> x = -1 => -4/3, y'(-1) = -1

Phương trình tiếp tuyến của đồ thị hàm số tại điểm x = -1 là: $y\ =\ \left(-1\right).\left(x+1\right)-\frac{4}{3}=\ -x-\frac{7}{3}$ $y\ =\ \left(-1\right).\left(x+1\right)-\frac{4}{3}=\ -x-\frac{7}{3}$

Chọn đáp án A.

Câu 7:

Ta có y' = x² - 4x + 3. Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.

Xét y' = 3 <=> x² - 4x = 0

x = 0 ⇒ y = 1

x = 4 ⇒ y = 7/3

Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1

Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là y = 3x - 29/3 .

Chọn đáp án D.

Câu 8:

Xét phương trình hoành độ giao điểm $x+1=\frac{2x+4}{x-1}$ $x+1=\frac{2x+4}{x-1}$ ⇒ x² - 2x - 5 = 0

Giao điểm của hai đồ thị hàm số là M(x₁; y₁), N(x₂; y₂) với x₁, x₂ là nghiệm phương trình (1). Do đó

$x_i=\frac{x_1+x_2}{2}=\ \frac{2}{2}=1$ $x_i=\frac{x_1+x_2}{2}=\ \frac{2}{2}=1$

Chọn đáp án B.

Câu 9:

Xét hàm số

y = f(x) = x³ + 3x² (C)

Đồ thị hàm số có dạng như hình bên.

Khảo sát sự biến thiên và vẽ đồ thị hàm số

x³ + 3x² = m có ba nghiệm phân biệt

<=> Đường thẳng y = m cắt đồ thị (C) tại ba điểm phân biệt <=> 0 < m < 4

Chọn đáp án D.

Câu 10:

Ta có: a = 2 > 0; y' = 6x² - 6(m + 1)x + 6(m + 1)² = 6[x² - (m + 1)x + (m + 1)²]

Δ = -3(m + 1)² ≤ 0 ∀x ∈ R => y' = 0 vô nghiệm hoặc nghiệm kép

Câu 11:

Ta có a = 1 > 0; => y’= 0 có một nghiệm x = 0.

Câu 13:

Đồ thị hàm số cắt đường thẳng y= 3, y=-4 tại một điểm ; cắt trục hoành và đường thẳng y = 5/3 tại 3 điểm.

Câu 14:

y' = 3x² . Đường thẳng y = 3x + m là tiếp tuyến của đường cong y = x³ + 2

Nếu y' = 3 ⇒ x = 1 ⇒ y = 3; x = -1 ⇒ y = 1

Tiếp tuyến của đường cong tại A(1;3) là y=3x.

Tiếp tuyến của đường cong tại B(-1;1) là y=3x+4.

Do đó m ∈ {0; 4}

Câu 15:

Ta có y’=-2x; y’(1)=-2. Phương trình tiếp tuyến của y = 4 - x² tại điểm y(1,3) là:

(d):y= -2(x-1)+3=-2x+5.

Đường thẳng (d) cắt trục hoành tại điểm A(5/2; 0) và cắt trục tung tại B(0;5).

Diện tích tam giác OAB vuông tại O là $S\ =\ \frac{1}{2}.\frac{5}{2}.5=\frac{25}{4}$ $S\ =\ \frac{1}{2}.\frac{5}{2}.5=\frac{25}{4}$

Câu 16:

Đường thẳng (d) có hệ số góc là k đi qua M(1;3) y=k(x-1)+3 .(d) tiếp xúc với đồ thì hàm số <=> hệ phương trình có nghiệm

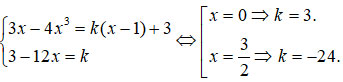
Khảo sát sự biến thiên và vẽ đồ thị hàm số

Do đó có tối đa hai tiếp tuyến đi qua điểm M(1;3).

Câu 17:

Xét hàm số y = x⁴ - 2x² + 3 ( C )

Đồ thị có dạng như hình (1)

x⁴ - 2x² + 3 -m² + 2m = 0 có đúng ba nghiệm phân biệt <=> Đường thẳng y = m² + 2m cắt đồ thị C tại ba điểm phân biệt

⇔ m² = 2m = 3 ⇔ m = -3; m = 1

Khảo sát sự biến thiên và vẽ đồ thị hàm số

Câu 18:

Đồ thị hàm số y = |x|³ - 2x² + |x| + 1 có dạng như hình (2)

Dựa vào đồ thị với m > 0 phương trình có tối thiểu 0 nghiệm.

Câu 19:

sin²x + cosx = m <=> -cosx²x + cosx + 1 = 0

Đặt t= cos x =>

=>f’(t)=-2t+1.

Do x ∈ [0; π] => t ∈ [-1; 1]

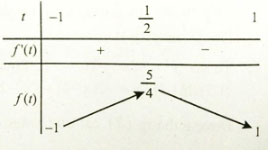
Khảo sát sự biến thiên và vẽ đồ thị hàm số

Từ bảng biến thiên ta có m ∈ (-1; 1) thì f(t)=m có một nghiệm

Trên đây VnDoc.com vừa giới thiệu tới các bạn Trắc nghiệm Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số, mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 12. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...

Mời bạn đọc cùng tham gia nhóm Tài liệu học tập lớp 12 để có thêm tài liệu học tập nhé

Mời các bạn cùng tham khảo thêm tài liệu về việc khảo sát sự biến thiên và vẽ đồ thị hàm số:

Chia sẻ, đánh giá bài viết

2

2.196

Bài trước

Bài sau