Giải bài tập trang 9, 10 SGK Giải tích lớp 12: Sự đồng biến, nghịch biến của hàm số

Giải bài tập trang 9, 10 SGK Giải tích lớp 12: Sự đồng biến, nghịch biến của hàm số là tài liệu tham khảo hay dành cho các em học sinh tham khảo, hướng dẫn giải chi tiết bài 1 trang 9; bài 2, 3, 4 trang 10 SGK giải tích lớp 12. Chúc các em học tốt môn Toán lớp 12. Mời các bạn cùng tham khảo chi tiết tại đây nhé.

• Bài tập trắc nghiệm khảo sát hàm số (Có đáp án)
• Bài tập trắc nghiệm tính đơn điệu của hàm số

Giải bài 1, 2, 3, 4 trang 9, 10 SGK giải tích lớp 12 (Sự đồng biến, nghịch biến của hàm số)

Bài 1 trang 9 SGK Giải tích lớp 12

Xét sự đồng biến, nghịch biến của các hàm số:

a) y = 4 + 3x – x²; b) y = 1/3x³ + 3x² – 7x – 2;

c) y = x⁴ – 2x² + 3; d) y = -x³ + x² – 5.

Đáp án và Hướng dẫn giải bài 1:

1. a) Tập xác định: D = R;

y' = 3 – 2x => y' = 0 ⇔ x = 3/2

Ta có Bảng biến thiên:

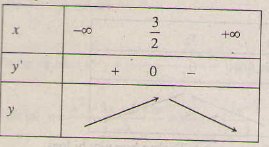
Hàm số đồng biến trên khoảng (-∞; 3/2); nghịch biến trên khoảng (3/2; +∞).

b) Tập xác định: D = R;

y' = x² + 6x – 7 => y' = 0 ⇔ x = 1, x = -7.

Bảng biến thiên:

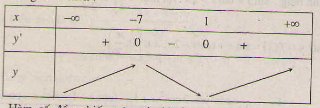
Hàm số đồng biến trên các khoảng (-∞; -7), (1; +∞); nghịch biến trên các khoảng (-7; 1).

c) Tập xác định: D = R.

y' = 4x³ – 4x = 4x(x² – 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.

Bảng biến thiên: (Học sinh tự vẽ)

Hàm số đồng biến trên các khoảng (-1; 0), (; +∞); nghịch biến trên các khoảng (-∞; -1), (0; 1).

d) Tập xác định: D = R.

y' = -3x² + 2x => y' = 0 ⇔ x = 0, x = 2/3.

Bảng biến thiên:

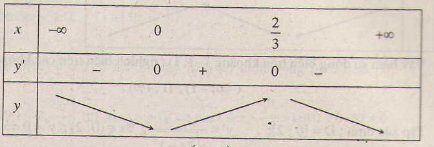
Hàm số đồng biến trên khoảng (0; 2/3); nghịch biến trên các khoảng (-∞; 0), (2/3; +∞).

Bài 2 trang 10 SGK Giải tích lớp 12

Tìm các khoảng đơn điệu của các hàm số:

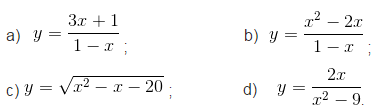
Đáp án và Hướng dẫn giải bài 2:

a) Tập xác định: D = R\{ 1 }.

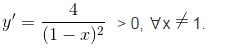
Hàm số đồng biến trên các khoảng: (-∞; 1), (1; +∞).

b) Tập xác định: D = R\{1}.

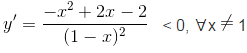
Hàm số nghịch biến trên các khoảng: (-∞; 1), (1; +∞).

c) Tập xác định: D = (-∞; -4] ∪ [5; +∞).

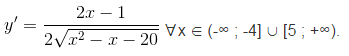
Với x ∈ (-∞; -4) thì y' < 0; với x ∈ (5; +∞) thì y' > 0. Vậy hàm số nghịch biến trên khoảng (-∞; -4) và đồng biến trên khoảng (5; +∞).

d) Tập xác định: D = R\{-3; 3}.

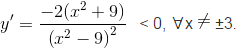
Hàm số nghịch biến trên các khoảng: (-∞; -3), (-3; 3), (3; +∞).

Bài 3 trang 10 SGK Giải tích lớp 12

Chứng minh rằng hàm số y = đồng biến trên khoảng (-1; 1) và nghịch biến trên các khoảng (-∞ ; -1) và (1; +∞).

Đáp án và Hướng dẫn giải bài 3:

Tập xác định: D = R. y' = 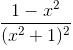⇒ y' = 0 ⇔ x = -1 hoặc x = 1.

Bảng biến thiên:

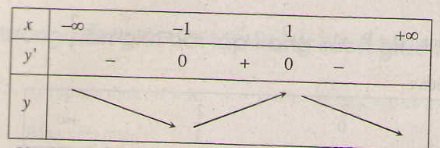
Vậy hàm số đồng biến trên khoảng (-1; 1); nghịch biến trên các khoảng (-∞; -1), (1; +∞).

Bài 4 trang 10 SGK Giải tích lớp 12

Chứng minh rằng hàm số y = đồng biến trên khoảng (0; 1) và nghịch biến trên các khoảng (1; 2).

Đáp án và Hướng dẫn giải bài 4:

Tập xác định: D = [0; 2]; y' = , ∀x ∈ (0; 2); y' = 0 ⇔ x = 1.

Bảng biến thiên:

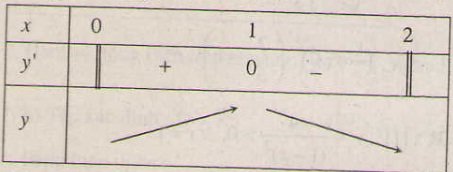
Vậy hàm số đồng biến trên khoảng (0; 1) và nghịch biến trên khoảng (1; 2).

Bài 5 trang 10 SGK Giải tích lớp 12

Chứng minh các bất đẳng thức sau:

a) tanx > x (0 < x < π/2);

b) tanx > x + x³/3 (0 < x <π/2).

Đáp án và Hướng dẫn giải bài 5:

a) Xét hàm số y = f(x) = tanx – x với x ∈ [0; π/2).

Ta có: y' = – 1 ≥ 0, x ∈ [0;π/2); y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0; π/2).

Từ đó ∀x ∈ (0; π/2) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.

b) Xét hàm số y = g(x) = tanx – x – x³/3. với x ∈ [0; π/2).

Ta có: y' = – 1 – x² = 1 + tan²x – 1 – x2 = tan²x – x²

= (tanx – x)(tanx + x), ∀x ∈ [0;π/2 ).

Vì ∀x ∈ [0; π/2) nên tanx + x ≥ 0 và tanx – x > 0 (theo câu a). Do đó y' ≥ 0, ∀x ∈ [0; π/2). Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0; π/2). Từ đó: ∀x ∈ [0; π/2) thì g(x) > g(0) ⇔ tanx – x – x³/3 > tan0 – 0 – 0 = 0 hay tanx > x + x³/3.

----------------------------------------

Bài tiếp theo: Giải bài tập trang 18 SGK Giải tích lớp 12: Cực trị của hàm số

Trên đây VnDoc.com vừa giới thiệu tới các bạn Giải bài tập trang 9, 10 SGK Giải tích lớp 12: Sự đồng biến, nghịch biến của hàm số, mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 12. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...