Cực trị của hàm số: Lý thuyết cực trị hàm số Toán 12 chương 1
Toán 12 chương 1: Cực trị của hàm số
Để giúp các bạn học sinh lớp 12 học tập hiệu quả hơn môn Toán, VnDoc.com đã tổng hợp chi tiết lý thuyết chương 1 cực trị của đạo hàm, qua bộ tài liệu sẽ giúp các bạn học sinh vận dụng giải bài tập Toán 12 chương 1 nhanh và chính xác nhất. Mời các bạn học sinh và thầy cô tham khảo.
- Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
- Trắc nghiệm Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
- Giải bài tập trang 18 SGK Giải tích lớp 12: Cực trị của hàm số
- Trắc nghiệm Toán 12 chương 1: Cực trị của hàm số
VnDoc.com xin gửi tới bạn đọc bài viết Cực trị của hàm số: Lý thuyết cực trị hàm số Toán 12 chương 1 để bạn đọc cùng tham khảo. Bài viết nêu tóm tắt lại nội cung lý thuyết của cực trị hàm số, các định lý của cực trị hàm số... Mời các bạn cùng tham khảo chi tiết và tải về tại đây.
Lý thuyết Toán 12 chương 1: Cực trị của hàm số
Cho hàm số xác định và liên tục trên khoảng (a;b) và x0 ∈ (a; b)
• Nếu tồn tại h > 0 sao cho f(x) < f(x0) và ∀x ∈(x0 - h; x0 + h) và x ≠ x0 thì ta nói f đạt cực đại tại x0.
• Nếu tồn tại h > 0 sao cho f(x) > f(x0) và ∀x ∈(x0 - h; x0 + h) và x ≠ x0 thì ta nói f đạt cực tiểu tại x0.
Khi đó:
+ x0 là điểm cực trị của hàm số.
+ f(x0) là giá trị cực trị của hàm số.
+ M(x0, f(x0)) là điểm cực trị của đồ thị hàm số.
Điều kiện cần và đủ để hàm số đạt cực trị
Điều kiện cần. Nếu hàm số f(x) đạt cực trị tại x0 và hàm số f(x) có đạo hàm tại điểm x0 thì f'(x0)= 0 .
Ghi chú: Hàm số f(x) có thể đạt cực trị tại một điểm mà tại đó nó không có đạo hàm.
Điều kiện đủ. Giả sử hàm số f(x) xác định trên (a; b) và x0 ∈ (a; b)
Định lí 1: Nếu f(x) có đạo hàm trên (a; b)\{x0} và với h > 0 sao cho (x0 - h; x0 + h) ⊂ (a; b) ta có
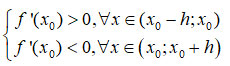
=> x0 là điểm cực đại của hàm số.
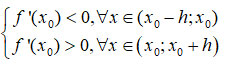
=> x0 là điểm cực tiểu của hàm số.
Định lí 2: Giả sử hàm số f(x) có đạo hàm cấp hai trên (a;b)
=> x0 là điểm cực tiểu của hàm số.
Trên đây VnDoc.com vừa giới thiệu tới các bạn Cực trị của hàm số: Lý thuyết cực trị hàm số Toán 12 chương 1, mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 12. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...
Mời bạn đọc cùng tham gia nhóm Tài liệu học tập lớp 12 để có thêm tài liệu học tập nhé
Mời bạn đọc cùng tham khảo thêm các tài liệu về cực trị của hàm số:
