VnDoc.com

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số

Bài tập trắc nghiệm môn Toán lớp 12 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại File: PDF

Phân loại: Tài liệu Tính phí

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số

HÀM BẬC BA
HÀM BẬC BỐN TRÙNG PHƯƠNG
HÀM PHÂN THỨC
HÀM BẬC HAI, HÀM CHỨA CĂN, HÀM LƯỢNG GIÁC, LOGARIT

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số tổng hợp các bài tập trắc nghiệm về tính đơn điệu của các dạng hàm số: hàm bậc ba, hàm bậc bốn, hàm phân thức, hàm chứa căn, hàm lượng giác... Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.

SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

HÀM BẬC BA

* Tìm các khoảng đơn điệu của hàm số

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số

Câu 19. Cho hàm số $y = \frac{1}{3}{x^3} - \frac{{m{x^2}}}{2} + 2x + 2016$ (với m là tham số). Với giá trị nào của tham số m, hàm số luôn đồng biến trên tập xác định?

A. $m = 2\sqrt 2$ B. $\left| m \right| \leqslant 2\sqrt 2$

C. $\left[ \begin{gathered} m \leqslant - 2\sqrt 2 \hfill \\ m \geqslant 2\sqrt 2 \hfill \\ \end{gathered} \right.$ D. Một kết quả khác

Câu 20. Cho hàm số $y = {x^3} + \left( {m + 2} \right){x^2} - \left( {m - 1} \right)x - 2$ (với m là tham số). Với giá trị nào của m thì hàm số đồng biến trên tập xác định:

A. $\frac{{ - 7 - \sqrt {45} }}{2} \leqslant m \leqslant \frac{{ - 7 + \sqrt {45} }}{2}$

B. $\frac{{ - 7 - \sqrt {45} }}{2} < m < \frac{{7 + \sqrt {45} }}{2}$

C. $\frac{{ - 7 - \sqrt {45} }}{2} < m < \frac{{ - 7 + \sqrt {45} }}{2}$

D. $\frac{{ - 7 - \sqrt {45} }}{2} \leqslant m \leqslant \frac{{7 + \sqrt {45} }}{2}$

Câu 21. Định tham số m để hàm số $y = \frac{{1 - m}}{3}{x^3} - 2\left( {2 - x} \right){x^2} + 2\left( {2 - m} \right)x + 5$ luôn nghịch biến khi:

A. B.

C. D. $2 \leqslant m \leqslant 3$

Câu 22. Với điều kiện nào của tham số m thì hàm số $y = m{x^3} - \left( {2m - 1} \right){x^2} + \left( {m - 2} \right)x - 2$ luôn đồng biến trên tập xác định của nó?

A. B. $m \geqslant 0$ C. $m \leqslant 0$ D.

Câu 23. Cho hàm số $y = m{x^3} - \left( {2m - 1} \right){x^2} + mx - 7$ (với m là tham số). Có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho nghịch biến trên ?

A. Không có giá trị B. 2 C. 0 D. Vô số giá trị

Tìm điều kiện để hàm số đơn điệu trên khoảng K cho trước

Câu 24. Hàm số $y = {x^3} - 3mx + 5$ nghịch biến trên khoảng (-1; 1) thì giá trị tham số m bằng:

A. 1 B. 2 C. 3 D. -1

Câu 25. Với giá trị nào của hàm số $y = {x^3} + 3{x^2} + \left( {m + 1} \right)x + 4m$ nghịch biến trên khoảng (-1; 1)?

A. B. C. $m \leqslant - 10$ D.

Câu 26. Tìm m để hàm số $y = - \frac{1}{3}{x^3} + \left( {m - 1} \right){x^2} + \left( {m + 3} \right)x - 10$ đồng biến trên khoảng (0; 3)?

A. $m \geqslant \frac{{12}}{7}$ B. $m < \frac{{12}}{7}$ C. $m \in \mathbb{R}$ D. $m > \frac{7}{{12}}$

Câu 27. Hàm số $y = {x^3} - 3{x^2} + mx + 1$ đồng biến trên khoảng $\left( {0; + \infty } \right)$ khi:

A. $m \leqslant 0$ B. $m \leqslant 3$ C. $m \geqslant 3$ D. $m \geqslant 0$

Câu 28. Hàm số $y = 2{x^3} - 3\left( {2m + 1} \right){x^2} + 6m\left( {m + 1} \right)x + 1$ đồng biến trên khoảng $\left( {2; + \infty } \right)$ khi:

A. B. $m \geqslant 1$ C. D. $m \leqslant 1$

Câu 29. Cho hàm số $y = {x^3} + 3{x^2} - mx - 4{\text{ }}\left( 1 \right)$ (với m là tham số). Tìm tất cả các giá trị của tham số m để hàm số (1) đã cho đồng biến trên khoảng $\left( { - \infty ;0} \right)$ ?

A. $m \leqslant 1$ B. $m \leqslant - 3$ C. D. $m \leqslant 3$

Câu 30. Tìm tất cả các giá trị thực của tham số m để hàm số $y = {x^3} - 2m{x^2} + m$ đồng biến trên khoảng $\left( { - \infty ;0} \right)$ ?

A. $m \geqslant 0$ B. $m \leqslant 0$ C. Không có m D. Mọi $m \in \mathbb{R}$

HÀM BẬC BỐN TRÙNG PHƯƠNG

* Tìm các khoảng đơn điệu của hàm số

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số

HÀM PHÂN THỨC

* Tìm các khoảng đơn điệu của hàm số

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số

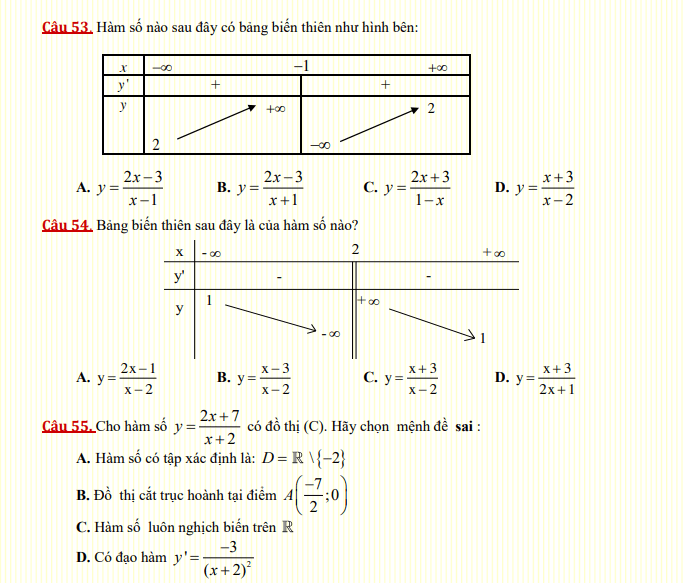
Câu 56. Cho hàm số $y = f(x) = \frac{ax + b}{cx + d}\ (ac \neq 0,ad - bc \neq 0)$ và là tập xác định của hàm số. Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên từng khoảng xác định, khi $y' > 0\forall x \in D$

B. Hàm số đồng biến trên từng khoảng xác định, khi $y' \geq 0\forall x \in D$

C. Hàm số nghịch biến trên từng khoảng của tập xác định, khi $y' < 0\forall x \in \mathbb{R}$

D. Hàm số nghịch biến trên từng khoảng của tập xác định, khi $y' \leq 0\forall x \in \mathbb{R}$

Câu 57. Cho hàm số $y = \frac{x + 1}{x - 1}$ . Chọn khẳng định đúng.

A. Hàm số nghịch biến trên các khoảng $( - \infty; - 1)$ và $( - 1; + \infty)$

B. Hàm số đồng biến trên các khoảng $( - \infty; - 1)$ và $( - 1; + \infty)$

C. Hàm số nghịch biến trên các khoảng $( - \infty;1)$ và $(1; + \infty)$

D. Hàm số đồng biến trên các khoảng $( - \infty;1)$ và $(1; + \infty)$

Câu 58. Cho hàm số $y = \frac{4}{x - 2}$ . Khẳng định đúng là:

A. Nghịch biến trên $\mathbb{R}$ .

B. Nghịch biến trên $D = \mathbb{R} \smallsetminus \{ 2\}$

C. Nghịch biến trên các khoảng $( - \infty;2);(2; + \infty)$ .

D. Đồng biến trên các $( - \infty;2);(2; + \infty)$ .

Câu 59. Kết luận nào sau đây về tính đơn điệu của hàm số $y = \frac{2x + 1}{x + 1}$ là đúng?

A. Hàm số đồng biến trên các khoảng $( - \infty; - 1)$ và $( - 1; + \infty)$ .

B. Hàm số luôn luôn đồng biến trên $\mathbb{R} \smallsetminus \{ - 1\}$ .

C. Hàm số nghịch biến trên các khoảng $( - \infty; - 1)$ và $( - 1; + \infty)$ .

D. Hàm số luôn luôn nghịch biến trên $\mathbb{R} \smallsetminus \{ - 1\}$ .

Câu 60. Cho hàm số $y = \frac{2x + 1}{x - 1}$ . Khẳng định nào sau đây là khẳng định sai?

A. Đồ thị hàm số có tiệm cận đứng là .

B. Hàm số không xác định tại điểm .

C. Hàm số nghịch biến trên $\mathbb{R}$ .

D. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng $- \frac{1}{2}$ .

Câu61. Các khoảng đơn điệu của hàm số $y = \frac{x^{2} + x - 1}{x - 1}$ là:

A. Đồng biến trên các khoảng $( - \infty;0)$ và $(2; + \infty)$ . Nghịch biến trên các khoảng và .

B. Đồng biến trên khoảng $( - \infty;1)$ . Nghịch biến trên khoảng .

C. Đồng biến trên khoảng $(2; + \infty)$ . Nghịch biến trên khoảng .

D. Đồng biến trên khoảng $(2; + \infty)$ . Nghịch biến trên khoảng .

Câu 62. Cho hàm số $y = \frac{x^{2} + 2x - 3}{x + 1}$ . Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $( - \infty; - 1)$ và nghịch biến trên khoảng $( - 1; + \infty)$ .

B. Hàm số nghịch biến trên $\mathbb{R}$ .

C. Hàm số đồng biến trên khoảng .

D. Hàm số nghịch biến trên các khoảng $( - \infty; - 1)$ và $( - 1; + \infty)$ .

Câu 63. Giá trị nào của m thì hàm số $y = \frac{x + m}{x - 2}$ nghịch biến trên từng khoảng xác định:

A. . B. $m \leq - 2$ . C. . D. $m \geq - 2$ .

Câu 64. Hàm số $y = \frac{mx + 7m - 8}{x - m}$ . luôn đồng biến trên từng khoảng xác định với m?

A. B. $- 8 \leq m \leq 1$ C. D. $- 4 \leq m \leq 1$

Câu 65. Tìm các giá trị thực của tham số m để hàm số $y = \frac{{{x^2} - mx + 2}}{{x - 1}}$ đồng biến trên từng khoảng xác định của nó?

A. $m \geqslant 3$ B.

C. $- 2\sqrt 2 \leqslant m \leqslant 2\sqrt 2$ D. $m < - 2\sqrt 2$ và $m > 2\sqrt 2$

Câu 66. Tìm tất cả cả các giá trị thực của tham số m để hàm số $y = \frac{{x + m}}{{x + 1}}$ đồng biến trên từng khoảng xác định của nó?

A. B. $m \leqslant 1$ C. D.

Câu 67. Hàm số $y = \frac{x}{{x - m}}$ đồng biến trên $\left( {2; + \infty } \right)$ khi và chỉ khi:

A. B. $m \leqslant 0$ C. D. $m \leqslant 2$

Câu 68. Các giá trị của tham số m để hàm số $y = \frac{{mx + 25}}{{x + m}}$ nghịch biến trên khoảng $\left( { - \infty ;1} \right)$ là:

A. $- 5 \leqslant m \leqslant 5$ B. $- 5 < m \leqslant - 1$

C. D. $m \geqslant - 1$

Câu 69. Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{{2 + mx}}{{2x + m}}$ nghịch biến trên từng khoảng xác định của nó?

A. $m \leqslant - 2$ và $m \geqslant 2$ B.

C. $- 2 \leqslant m \leqslant 2$ D. hoặc

HÀM BẬC HAI, HÀM CHỨA CĂN, HÀM LƯỢNG GIÁC, LOGARIT

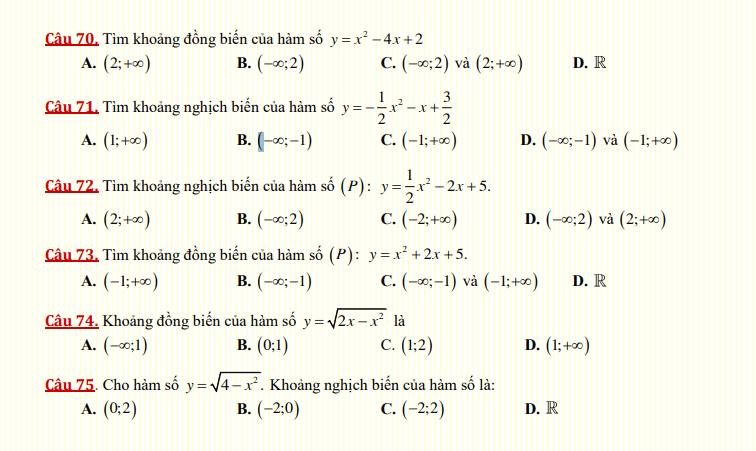
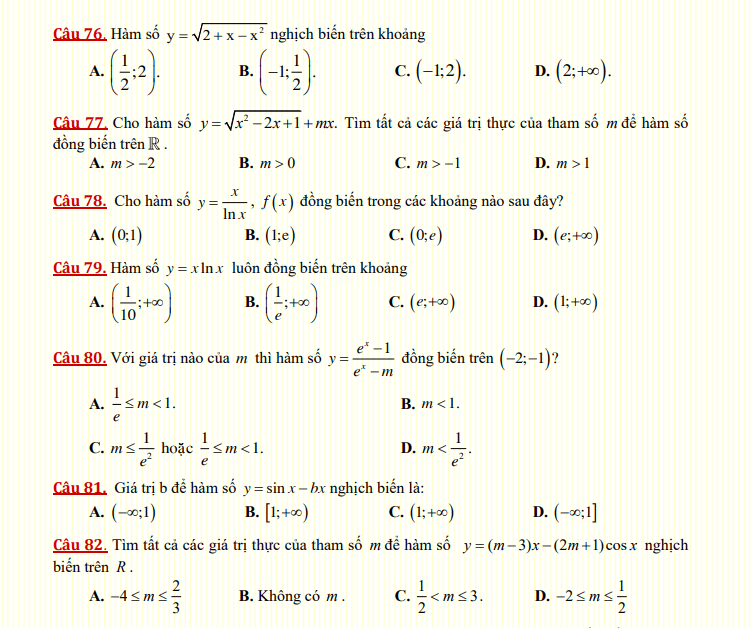
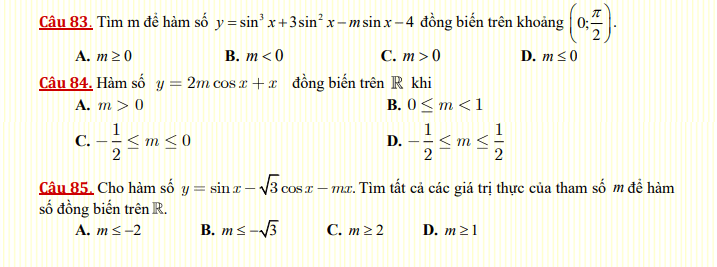
Đáp án bài tập trắc nghiệm

1 - C	2 - D	3 - C	4 - A	5 - C	6 - B	7 - A	8 - B	9 - D	10 - C
11 - D	12 - A	13 - D	14 - A	15 - B	16 - D	17 - C	18 - D	19 - B	20 - D
21 - D	22 - A	23 - A	24 - A	25 - C	26 - A	27 - C	28 - D	29 - B	30 - A
31 - B	32 - D	33 - A	34 - C	35 - D	36 - A	37 - A	38 - C	39 - D	40 - A
41 - A	42 - D	43 - D	44 - A	45 - B	46 - D	47 - A	48 - A	49 - A	50 - D
51 - D	52 - D	53 - B	54 - C	55 - C	56 - A	57 - C	58 - C	59 - A	60 - C
61 - A	62 - C	62 - C	64 - A	65 - A	66 - A	67 - A	68 - B	69 - B	70 - A
71 - C	72 - B	73 - A	74 - B	75 - A	76 - A	77 - D	78 - D	79 - B	80 - C
81 - B	82 - A	83 - C	84 - D	85 - A	86 - C	87 - B	88 - A	89 - A	90 - A
91 - B	92 - A	93 - D

Mời các bạn tải file đầy đủ về tham khảo.

Trên đây VnDoc.com vừa giới thiệu tới các bạn Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số. Bài viết cho chúng ta thấy được những câu hỏi trắc nghiệm môn Toán lớp 12 về sự đồng biến, nghịch biến của hàm số. Mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 12. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, Tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...

Tải về

Chọn file muốn tải về:

Câu hỏi trắc nghiệm môn Toán lớp 12: Sự đồng biến, nghịch biến của hàm số

928,7 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Đen2017

30

56.955

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!