Toán 12 Bài 4: Đường tiệm cận của đồ thị Hàm số
Đường tiệm cận của đồ thị hàm số Toán lớp 12
Trong Toán 12, việc nghiên cứu đường tiệm cận của đồ thị hàm số là một trong những nội dung quan trọng, giúp học sinh hiểu rõ hơn về hình dạng và sự biến thiên của đồ thị. Đường tiệm cận không chỉ là kiến thức cơ bản của giải tích mà còn thường xuyên xuất hiện trong các đề thi THPT quốc gia môn Toán.
Ở bài học Toán 12 Bài 4: Đường tiệm cận của đồ thị hàm số, học sinh sẽ được tìm hiểu khái niệm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên; công thức xác định và phương pháp nhận dạng trong từng trường hợp cụ thể. Bên cạnh đó, việc nắm chắc cách vẽ đường tiệm cận của đồ thị hàm số sẽ giúp học sinh dễ dàng phác thảo đồ thị, phân tích tính chất hàm số và xử lý các dạng toán liên quan một cách nhanh chóng, chính xác. Đây chính là nền tảng để học tốt các chuyên đề nâng cao và tự tin trong các kỳ thi quan trọng.
- Giải bài tập trang 30 SGK Giải tích lớp 12: Đường tiệm cận
- Bài tập trắc nghiệm đường tiệm cận
- Câu hỏi trắc nghiệm môn Toán lớp 12: Đường tiện cận
A. Lý thuyết Đường tiệm cận của đồ thị hàm số
1. Cách tìm đường tiệm cận
a. Để tìm đường tiệm cận của hàm số y = f(x) ta dựa vào tập xác định D để biết số giới hạn phải tìm. Nếu tập xác định D có đầu mút là khoảng thì phải tìm giới hạn của hàm số khi x tiến đến đầu mút đó.
Ví dụ: 
\(D=[a,b)\) thì phải tính \(\lim_{x\rightarrow \infty} f(x)\) hay \(D=(-\infty,a]\cup(b,+\infty)\) thì ta phải tìm bốn giới hạn là \(\lim_{x\rightarrow -\infty} f(x),\lim_{x\rightarrow +\infty} f(x),\lim_{x\rightarrow b^+} f(x),\lim_{x\rightarrow a^-} f(x)\)
b. Để tìm đường tiệm cận ngang ta phải có giới hạn của hàm số ở vô tận
Nếu \(\lim_{x\rightarrow \infty} f(x)=y_0\) thì \((\delta):y=y_0\) là tiệm cận ngang của đồ thị hàm số \((C):y=f(x)\)
- Để tìm đường tiệm cận đứng thì hàm số phải ra vô tận khi x tiến đến một giá trị x:
nếu \(\lim_{x\rightarrow x_0^+} f(x)=\pm \infty\) hay \(\lim_{x\rightarrow x_0^-} f(x)=\pm \infty\) thì \(\delta:x=x_0\) là tiệm cận đứng của \((C):y=f(x)\).
c. Để tìm đường tiệm cận xiên của (C): y = f(x), trước hết ta phải có điều kiện:
- Điều kiện tìm đường tiệm cận xiên: \(\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=\pm \infty\) hoặc \(\underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)=\pm \infty\)
Tìm tiệm cận xiên có 2 cách:
Cách 1: Phân tích \(y=f\left( x \right)\) thành dạng \(y=ax+b+g\left( x \right)\) với \(\underset{x\to \pm \infty }{\mathop{\lim }}\,g\left( x \right)=0\) thì \(y=ax+b,\left( a\ne 0 \right)\) là đường tiệm cận xiên của đồ thị hàm số \(y=f\left( x \right)\).
Cách 2: Giả sử tiệm cận xiên của đồ thị hàm số là \(y=ax+b\), ta sẽ tìm a, b theo công thức:
\(\left\{ \begin{matrix}
a=\underset{x\to \pm \infty }{\mathop{\lim }}\,\dfrac{f\left( x \right)}{x} \\
b=\underset{x\to \pm \infty }{\mathop{\lim }}\,\left[ f\left( x \right)-ax \right] \\
\end{matrix} \right.\)
Khi đó đường thẳng \(y=ax+b,\left( a\ne 0 \right)\) là phương trình đường tiệm cận xiên của đồ thị hàm số.
2. Đường tiệm cận của một số hàm số thông dụng
- Hàm số \(y=\dfrac{ax+b}{cx+d}\) có hai đường tiệm cận đứng và ngang lần lượt có phương trình là: \(x=-\dfrac{c}{d}\) và \(y=\dfrac{a}{c}\)
- Với hàm số \(y=\dfrac{a^2+bx+c}{px+q}\)(không chia hết và a.p ≠ 0), ta chia đa thức để có:
\(y=\frac{a^2+bx+c}{px+q}=Ax+B+\frac{R}{px+q}\) thì hàm số có hai đường tiệm cận đứng và xiên lần lượt có phương trình là: \(x=\dfrac{-p}{q}\) và \(y=Ax+B\)
- Hàm hữu tỉ \(y=\dfrac{P(x)}{Q(x)}\) (không chia hết) có đường tiệm cận xiên khi bậc của tử lớn hơn bậc của mẫu một bậc.
- Hàm số \(y=\sqrt{ax^2+bx+c},\left(a>0\right)\) có thể viết dưới dạng:
\(y=\sqrt{a}\left | x+\dfrac{1}{2a} \right | +\xi (x)\) với \(\lim_{x\rightarrow \pm \infty} \xi (x)=0\)
Vậy hàm số có hai đường tiệm cận xiên \(y=\pm \sqrt{a}(x+\dfrac{b}{2a})\).
3. Ví dụ minh họa cách xác định đường tiệm cận của đồ thị hàm số
Ví dụ: Đồ thị hàm số: \(y=f(x)=\frac{x^2-4x+3}{x^2-9}\)có các đường tiệm cận với phương trình là kết quả nào sau đây?
| (A) x = 3, y = 1 | (B) x= 3, x = -3, y = 1 |
| (C) x = -3, y = 1 | (D) x = 3, y = 2x - 4 |
Hướng dẫn giải
Hàm số có tập xác định \(D=\mathbb{R} \setminus\left \{ -3,3 \right \}\), \(\lim_{x\rightarrow \pm \infty} f(x)=1\Rightarrow y=1\)
là đường tiệm cận ngang của đồ thị hàm số .
\(\lim_{x\rightarrow 3} \dfrac{x^2-4x+3}{x^2-9}=\lim_{x\rightarrow 3} \dfrac{(x-1)(x-3)}{(x-3)(x+3)}=\dfrac{1}{3}\) nên x = 3 không là tiệm cận đứng.
\(\lim_{x\rightarrow-3}f(x)=\infty\) vậy x = -3 là phương trình tiệm cận đứng
Chọn đáp án C.
Ví dụ: Cho hàm số \(y = f(x)\) có \(\lim_{x \rightarrow + \infty}f(x) = 0\) và \(\lim_{x \rightarrow - \infty}f(x) = +
\infty\). Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số nằm phía trên trục hoành.
C. Đồ thị hàm số có một tiệm cận ngang là trục hoành.
D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng \(y = 0.\)
Hướng dẫn giải
Ta có \(\lim_{x \rightarrow + \infty}f(x) =
0\overset{}{\rightarrow}y = 0\) là tiệm cận ngang.
Đáp án “Đồ thị hàm số nằm phía trên trục hoành.“ sai vì chọn hàm \(y = \left\{ \begin{matrix}
\left( \frac{1}{2} \right)^{x} & ;x \leq - 1 \\
- \left( \frac{1}{2} \right)^{x} & ;x \geq 1 \\
\end{matrix} \right.\).
Vậy ta chỉ có đáp án “Đồ thị hàm số có một tiệm cận ngang là trục hoành” đúng.
Ví dụ: Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\backslash\left\{ -
1 \right\}\), có bảng biến thiên như sau:
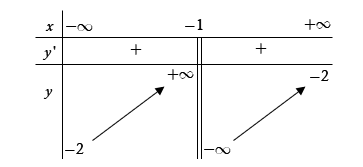
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số có tiệm cận đứng \(y = -
1\) và tiệm cận ngang \(x = -
2.\)
B. Đồ thị hàm số có duy nhất một tiệm cận.
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng \(x = -
1\) và tiệm cận ngang \(y = -
2.\)
Hướng dẫn giải
Từ bảng biến thiên, ta có:
\(\left\{ \begin{matrix}
\lim_{x \rightarrow ( - 1)^{-}}f(x) = + \infty \\
\lim_{x \rightarrow ( - 1)^{+}}f(x) = - \infty \\
\end{matrix} \right.\ \rightarrow x = - 1\) là TCĐ.
\(\left\{ \begin{matrix}
\lim_{x \rightarrow - \infty}y = - 2 \\
\lim_{x \rightarrow + \infty}y = - 2 \\
\end{matrix} \right.\ \rightarrow y = - 2\) là TCN.
Vậy đồ thị hàm số có tiệm cận đứng \(x = -
1\) và tiệm cận ngang \(y = -
2.\).
Ví dụ: Tìm giá trị thực của tham số \(m\) để đồ thị hàm sô \(y = \frac{mx - 1}{2x +
m}\) có đường tiệm cận đứng đi qua điểm \(M\left( - 1;\sqrt{2} \right).\)
A. \(m = 2\). B. \(m = 0\). C. \(m = \frac{1}{2}.\) D. \(m = \frac{\sqrt{2}}{2}\).
Hướng dẫn giải
TXĐ: \(D\mathbb{= R}\backslash\left\{ -
\frac{m}{2} \right\}\).
Ta có \(\left\{ \begin{matrix}
\lim_{x \rightarrow \left( - \frac{m}{2} \right)^{-}}y = \lim_{x
\rightarrow \left( - \frac{m}{2} \right)^{-}}\frac{mx - 1}{2x + m} = +
\infty \\
\lim_{x \rightarrow \left( - \frac{m}{2} \right)^{+}}y = \lim_{x
\rightarrow \left( - \frac{m}{2} \right)^{+}}\frac{mx - 1}{2x + m} = -
\infty \\
\end{matrix} \right.\ \rightarrow x = - \frac{m}{2}\) là TCĐ.
Do đó yêu cầu bài toán \(\Leftrightarrow -
\frac{m}{2} = - 1 \Leftrightarrow m = 2\).
Ví dụ: Tìm tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = \frac{x + 2}{x^{2} - 4x + m}\) có tiệm cận ngang mà không có tiệm cận đứng.
A. \(m = - 12.\) B. \(m > 4.\) C. \(m = - 12,m > 4.\) D. \(m \neq 4.\)
Hướng dẫn giải
Ta có \(\lim_{x \rightarrow \pm
\infty}\frac{x + 2}{x^{2} - 4x + m} = 0y = 0\) là tiệm cận ngang với mọi \(m\).
Do đó để đồ thị hàm số có tiệm cận ngang mà không có tiệm cận đứng thì phương trình \(x^{2} - 4x + m = 0\) vô nghiệm \(\Leftrightarrow \ \ \Delta'
< 0\ \ \Leftrightarrow \ \ m > 4\).
Nhận xét. Bạn đọc dễ nhầm lẫn mà xét thêm trường hợp mẫu thức \(x^{2} - 4x + m = 0\) có nghiệm \(x = - 2 \rightarrow m = - 12\). Điều này là sai, vì với \(m = - 12\) thì hàm số trở thành \(y = \frac{1}{x - 6}\). Đồ thị này vẫn còn tiệm cận đứng là \(x =
6\).
B. Giải SGK Toán 12 Bài 4
Trong Sách giáo khoa Toán lớp 12, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 12. Mời các bạn học sinh tham khảo:
C. Giải SBT Toán 12 Bài 4
Sách bài tập Toán 12 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:
D. Bài tập trắc nghiệm Tiệm cận của đồ thị hàm số
Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của bài Hàm số này, VnDoc xin gửi tới các bạn học sinh Tài liệu Tiệm cận của hàm số do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:
------------------------------------
Tóm lại, Toán 12 Bài 4: Đường tiệm cận của đồ thị hàm số không chỉ mang đến kiến thức lý thuyết về các loại tiệm cận mà còn trang bị cho học sinh kỹ năng nhận dạng và vẽ đồ thị một cách trực quan, khoa học. Đây là nội dung quan trọng, gắn liền với nhiều chuyên đề khác trong chương trình giải tích 12 và đặc biệt hữu ích trong việc giải quyết các dạng bài tập khảo sát hàm số, biện luận phương trình hay bất phương trình.
Hy vọng bài viết đã cung cấp cho bạn cái nhìn hệ thống về cách vẽ đường tiệm cận của đồ thị hàm số, từ lý thuyết đến bài tập ứng dụng. Để học tốt phần này, học sinh nên kết hợp học công thức, luyện vẽ đồ thị và giải nhiều dạng bài tập trong sách giáo khoa, sách nâng cao cũng như đề thi minh họa. Việc rèn luyện thường xuyên sẽ giúp bạn thành thạo kỹ năng, tăng tốc độ làm bài và tự tin chinh phục điểm cao trong kỳ thi THPT quốc gia môn Toán.
