Giải bài tập trang 18 SGK Giải tích lớp 12: Cực trị của hàm số
Giải bài tập trang 18 SGK Toán 12 bài 2 Đại số và Giải tích là bộ tài liệu hay đã được VnDoc.com tổng hợp dành cho các bạn học sinh lớp 12 tham khảo để rèn luyện giải nhanh các bài tập trong SGK một cách chính xác nhất. Mời các bạn và thầy cô tham khảo.
Giải bài tập trang 18 sgk Toán 12 bài 2
- Bài 1 trang 18 sách sgk Toán 12 Đại số và Giải tích
- Bài 2 trang 18 sách sgk Toán 12 Đại số và Giải tích
- Bài 3 trang 18 sách sgk Toán 12 Đại số và Giải tích
- Bài 4 trang 18 sách sgk Toán 12 Đại số và Giải tích
- Bài 5 trang 18 sách sgk Toán 12 Đại số và Giải tích
- Bài 6 trang 18 sách sgk Toán 12 Đại số và Giải tích
Bài 1 trang 18 sách sgk Toán 12 Đại số và Giải tích
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :
a) 
\(y{\rm{ }} = {\rm{ }}2{x^{3}} + {\rm{ }}3{x^2}-{\rm{ }}36x{\rm{ }}-{\rm{ }}10\)
b) \(y{\rm{ }} = {\rm{ }}x{^4} + {\rm{ }}2{x^2}-{\rm{ }}3\)
c) \(y = x + {1 \over x}\)
d) \(y{\rm{ }} = {\rm{ }}{x^3}{\left( {1{\rm{ }}-{\rm{ }}x} \right)^{2}}\)
e) \(y = \sqrt {{x^2} - x + 1}\)
Giải:
a) Tập xác định: \(D = \mathbb R\)
\(\eqalign{
& y' = 6{{\rm{x}}^2} + 6{\rm{x}} - 36;y' = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 2\left( {y = - 54} \right) \hfill \cr
x = - 3\left( {y = 71} \right) \hfill \cr} \right. \cr}\)
Bảng biến thiên:
Hàm số đạt cực trị tại x = -3\) và \(yCĐ = 71\)
Hàm số đạt cực tiểu tại x = 2 và yCT = -54
b) Tập xác định: \(D =\mathbb R\)
\(y' = 4{{\rm{x}}^3} + 4{\rm{x}} = 4{\rm{x}}\left( {{x^2} + 1} \right)\)
\(y' = 0 \Leftrightarrow x = 0\left( {y = - 3} \right)\)
Bảng biến thiên:
Hàm số có điểm cực tiểu tại x = 0 và yCT = -3
c) Tập xác định: D = R\0
\(\eqalign{
& y' = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}};y' = 0 \cr
& \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \matrix{
x = 1\left( {y = 2} \right) \hfill \cr
x = - 1\left( {y = - 2} \right) \hfill \cr} \right. \cr}\)
Bảng biến thiên
Hàm số đạt cực đại tại x = -1, yCĐ = -2
Hàm số đạt cực tiểu tại x = 1, yCT = 2
d) Tập xác định \(D = \mathbb R\)
\(y' = 3{{\rm{x}}^2}{\left( {1 - x} \right)^2} - 2{{\rm{x}}^3}\left( {1 - x} \right)
= {x^2}\left( {1 - x} \right)\left( {3 - 5{\rm{x}}} \right)\eqalign{
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 1\left( {y = 0} \right) \hfill \cr
x = {3 \over 5}\left( {y = {{108} \over {3125}}} \right) \hfill \cr
x = 0 \hfill \cr} \right. \cr}\)
Bảng biến thiên:
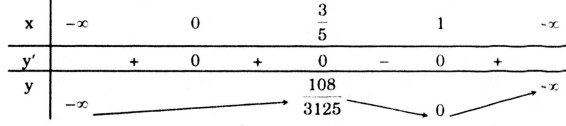
Hàm số đạt cực đại tại \(x = {3 \over 5};y = {{108} \over {3125}}\)
Hàm số đạt cực tiểu tại x = 1, yCT = 0
e) Vì \(x^2 – x + 1 > 0,\) ∀ ∈ \(\mathbb R\) nên tập xác định : \(D = \mathbb R\)
\(y' = {{2{\rm{x}} - 1} \over {2\sqrt {{x^2} - x + 1} }};y = 0 \Leftrightarrow x = {1 \over 2}\left( {y = {{\sqrt 3 } \over 2}} \right)\)
Bảng biến thiên:
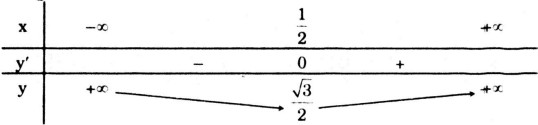
Hàm số đạt cực tiểu tại \(x = {1 \over 2};{y_{CT}} = {{\sqrt 3 } \over 2}\)
Bài 2 trang 18 sách sgk Toán 12 Đại số và Giải tích
. Áp dụng quy tắc II, hãy tìm các điểm cực trị của hàm số sau:
a) \(y{\rm{ }} = {\rm{ }}{x^4} - {\rm{ }}2{x^2} + {\rm{ }}1\)
b) \(y = sin2x – x\)
c) \(y = sinx + cosx\)
d) \(y{\rm{ }} = {\rm{ }}{x^5}-{\rm{ }}{x^3}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1\)
Giải:
a) \(y'{\rm{ }} = 4{x^3}-{\rm{ }}4x{\rm{ }} = {\rm{ }}4x({x^2} - {\rm{ }}1) ;
y' = 0⇔ 4xx^2 - 1) = 0 ⇔ x = 0, x = \pm 1\)
\(y'' = 12x^2-4\)
\(y''(0) = -4 < 0\) nên hàm số đạt cực đại tại x = 0
\(ycđ = y(0) = 1\)
\(y''(\pm 1) = 8 > 0\) nên hàm số đạt cực tiểu tại \(x = \pm1\)
\(yct = y(\pm1) = 0\)
b)\(y' = 2cos2x - 1y'=0\Leftrightarrow cos2x=\frac{1}{2}\Leftrightarrow 2x=\pm \frac{\pi }{3}+k2\pi\Leftrightarrow x=\pm \frac{\pi }{6}+k\pi .y'' = -4sin2x\)
\(y''\left ( \frac{\pi }{6} +k\pi \right )=-4sin\left ( \frac{\pi }{3} +k2\pi \right )=-2\sqrt{3}<0\) nên hàm số đạt cực đại tại các điểm \(x = \frac{\pi }{6}+ kπ\)
\(ycđ = sin(\frac{\pi }{3}+ k2π) - \frac{\pi }{6} - kπ = \frac{\sqrt{3}}{2}-\frac{\pi }{6}- kπ , k ∈\mathbb Z.\)
\(y''\left ( -\frac{\pi }{6} +k\pi \right )=-4sin\left (- \frac{\pi }{3} +k2\pi \right )=2\sqrt{3}>0\) nên hàm số đạt cực tiểu tại các điểm\(x =-\frac{\pi }{6}+ kπ\)
\(yct = sin(-\frac{\pi }{3}+ k2π) + \frac{\pi }{6} - kπ =-\frac{\sqrt{3}}{2}+\frac{\pi }{6} - kπ , k ∈\mathbb Z.\)
c) \(y = sinx + cosx = \sqrt{2}sin\left (x+\frac{\pi }{4} \right )\)
\(y' =\sqrt{2}cos\left (x+\frac{\pi }{4} \right )\)
\(y'=0\Leftrightarrow cos\left (x+\frac{\pi }{4} \right )=0\Leftrightarrow(x+\frac{\pi }{4} =\frac{\pi }{2}+k\pi \Leftrightarrow x=\frac{\pi }{4}+k\pi .\)
\(y''=-\sqrt{2}sin\left ( x+\frac{\pi }{4} \right ).\)
\(y''\left ( \frac{\pi }{4} +k\pi \right )=-\sqrt{2}sin\left ( \frac{\pi }{4}+k\pi +\frac{\pi }{4} \right )=-\sqrt{2}sin\left ( \frac{\pi }{2} +k\pi \right )=\left\{ \matrix{
- \sqrt 2 \text{ nếu k chẵn} \hfill \cr
\sqrt 2 \text{ nếu k lẻ} \hfill \cr} \right.\)
Do đó hàm số đạt cực đại tại các điểm \(x=\frac{\pi }{4}+k2\pi\)
đạt cực tiểu tại các điểm \(x=\frac{\pi }{4}+(2k+1)\pi (k\in \mathbb{Z}).\)
d)\(y'{\rm{ }} = {\rm{ }}5{x^4} - {\rm{ }}3{x^2} - {\rm{ }}2{\rm{ }} = {\rm{ }}({x^2} - {\rm{ }}1)(5{x^2} + {\rm{ }}2); y'{\rm{ }} = {\rm{ }}0 \Leftrightarrow {x^{2}} - {\rm{ }}1{\rm{ }} = {\rm{ }}0 \Leftrightarrow {\rm{ }}x{\rm{ }} = \pm 1\)
\(y''{\rm{ }} = {\rm{ }}20{x^{3}} - {\rm{ }}6x.
y''(1) = 14 > 0\) nên hàm số đạt cực tiểu tại x = 1,
\(yct = y(1) = -1\)
\(y''(-1) = -14 < 0\) hàm số đạt cực đại tại x = -1,
\(ycđ = y(-1) = 3\)
Bài 3 trang 18 sách sgk Toán 12 Đại số và Giải tích
Chứng minh rằng hàm số \(y=\sqrt{\left | x \right |}\) không có đạo hàm tại x = 0 nhưng vẫn đạt cực tiểu tại điểm đó.
Giải:
Đặt \(y=f(x)=\sqrt{\left | x \right |}\). Giả sử x > 0, ta có:
\(\underset{x\rightarrow 0^{+}}{lim}\frac{\sqrt{x}}{x}=\underset{x\rightarrow 0^{+}}{lim}\frac{1}{\sqrt{x}}=+\infty .\)
Do đó hàm số không có đạo hàm tại x = 0. Tuy nhiên hàm số đạt cực tiểu tại x = 0 vì\(f(x)=\sqrt{\left | x \right |}\geq 0=f(0),\forall x\in\mathbb R\)
Bài 4 trang 18 sách sgk Toán 12 Đại số và Giải tích
Chứng minh rằng với mọi giá trị của tham số m, hàm số \(y{\rm{ }} = {\rm{ }}{x^3}-{\rm{ }}m{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1\) luôn luôn có một điểm cực đại và một điểm cực tiểu.
Giải:
\(y{\rm{ }} = {\rm{ }}3{x^2}-{\rm{ }}2mx{\rm{ }}-{\rm{ }}2{\rm{ }},\Delta ' = {\rm{ }}{m^{2}} + {\rm{ }}6{\rm{ }} > {\rm{ }}0 nên y’ = 0\) có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.
Bài 5 trang 18 sách sgk Toán 12 Đại số và Giải tích
Tìm a và b để các cực trị của hàm số \(y=\frac{5}{3}a^{2}x^{3}+2ax^{2}-9x+b\) đều là những số dương và \(x_{0}=-\frac{5}{9}\)là điểm cực đại.
Giải:
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét \(a \ne 0\). Ta có :\(y{\rm{ }} = {\rm{ }}5{a^2}{x^2} + {\rm{ }}4ax{\rm{ }}-{\rm{ }}9; y’= 0 ⇔ x=-\frac{1}{a} hoặc x=-\frac{9}{5a}\)
- Xét a < 0 ta có bảng biến thiên :
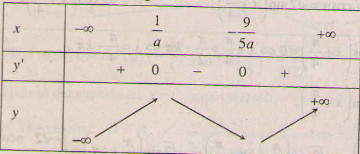
Theo giả thiết \(x_{0}=-\frac{5}{9}\) là điểm cực đại nên \(\frac{1}{a}=-\frac{5}{9}\Leftrightarrow a=\frac{9}{5}\). Theo yêu cầu bài toán thì
\(y_{(CT)}=y\left ( -\frac{9}{5a} \right )=y(1)>0
\Leftrightarrow \frac{5}{3}\cdot \left ( -\frac{9}{5} \right )^{2}+2\cdot \left ( -\frac{9}{5} \right )-9+b>0\Leftrightarrow b>\frac{36}{5}.\)
- Xét a > 0 ta có bảng biến thiên :
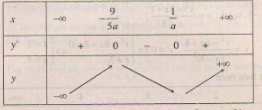
Vì \(x_{0}=-\frac{5}{9}\) là điểm cực đại nên \(-\frac{9}{5a}=-\frac{5}{9}\Leftrightarrow a=\frac{81}{25}\). Theo yêu cầu bài toán thì: \(y_{(ct)}=y\left ( \frac{1}{a} \right )=y\left ( \frac{25}{81} \right )>0\)
\(\Leftrightarrow \frac{5}{3}\cdot \left ( \frac{81}{25} \right )^{2}\left ( \frac{25}{81} \right )^{3}+2.\frac{81}{25}\cdot \left ( \frac{25}{81} \right )^{2}-9\cdot \frac{25}{81}+b>0\Leftrightarrow b>\frac{400}{243}.\)
Vậy các giá trị a, b cần tìm là:
\(\left\{\begin{matrix} a=-\frac{9}{5} & \\ b>\frac{36}{5} & \end{matrix}\right. hoặc \left\{\begin{matrix} a=\frac{81}{25} & \\ b>\frac{400}{243} & \end{matrix}\right.\)
Bài 6 trang 18 sách sgk Toán 12 Đại số và Giải tích
Xác định giá trị của tham số m để hàm số \(y=\frac{x^{2}+mx+1}{x+m}\) đạt cực đại tại x = 2
Giải:
Tập xác định : \(D=\mathbb{R}\setminus \left \{ -m \right \}\)
\(y'=\frac{2x^{2}+2mx+m^{2}-1}{(x+m)^{2}}.\)
Nếu hàm số đạt cực đại tại x = 2 thì:
\(y'(2) = 0⇔ {m^{2}} + {\rm{ }}4m{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0 ⇔ m=-1 hoặc m=-3\)
- Với m = -1, ta có : \(y=\frac{x^{2}-x+1}{x-1};\)
\(y'=\frac{x^{2}-2x}{(x-1)^{2}}; y'=0\Leftrightarrow \left\{\begin{matrix} x^{2} -2x=0& \\ x\neq 1 & \end{matrix}\right.\Leftrightarrow x=0 hoặc x=2\)
Ta có bảng biến thiên :
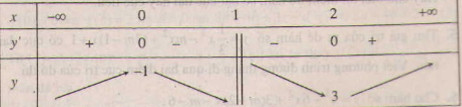
Trường hợp này ta thấy hàm số không đạt cực đại tại x = 2.
- Với m = -3, ta có: \(y=\frac{x^{2}3x+1}{x-3};\)
\(y'=\frac{x^{2}-6x+8}{(x-3)^{2}};y'=0\Leftrightarrow \left\{\begin{matrix} x^{2-6x+8=0} & \\ x\neq 3 & \end{matrix}\right.\Leftrightarrow x=2 hoặc x=4\)
Ta có bảng biến thiên :
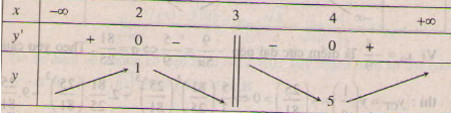
Trường hợp này ta thấy hàm số đạt cực đại tại x = 2.
Vậy m = -3 là giá trị cần tìm.
Tài liệu hướng dẫn các em giải các bài tập trong sách giáo khoa Toán 12 phần Cực trị của hàm số, giúp các em ôn luyện trong quá trình làm bài và củng cố kiến thức đã được học. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt kết quả cao trong học tập, tự tin bước vào các kì thi quan trọng.
VnDoc xin giới thiệu tới các em Giải bài tập trang 18 sgk Toán 12 Đại số và Giải tích để các em tham khảo. Tài liệu được trình bày ngắn gọn và dễ hiểu và bám sát kiến thức lí thuyết chương trình sgk Toán 12. Các em có thể tham khảo thêm các tài liệu khác tại mục Tài liệu học tập lớp 12 do VnDoc tổng hợp và đăng tải như: Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Hóa học 12, Trắc nghiệm Sinh học 12,...
