Bài tập trắc nghiệm sự tương giao giữa hai đồ thị (Có đáp án)
Trắc nghiệm Toán 12: Sự tương giao giữa hai đồ thị
Bài tập trắc nghiệm sự tương giao giữa hai đồ thị (Có đáp án) tổng hợp một số câu hỏi trắc nghiệm về giao điểm của các đồ thị hàm số. Tài liệu trắc nghiệm Toán 12 này có đáp án đi kèm, giúp các bạn luyện thi trắc nghiệm môn Toán hiệu quả, chuẩn bị sẵn sàng cho kỳ thi THPT Quốc gia.
Bài tập trắc nghiệm phương trình tiếp tuyến của đồ thị hàm số (Có đáp án)
Bài tập trắc nghiệm tính đơn điệu của hàm số
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 12, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 12 sau: Nhóm Tài liệu học tập lớp 12. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Câu 1: Cho hàm số y = x3 - 4x. Số giao điểm của đồ thị hàm số và trục Ox bằng
| A. 0 | B. 2 | C. 3 | D. 4 |
Câu 2: Số giao điểm của đường cong y = x3 - 2x2 + 2x + 1 và đường thẳng y = 1 - x bằng
| A. 0 | B. 2 | C. 3 | D. 1 |
Câu 3: Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong ![]() . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
. Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
| A. -5/2 | B. 1 | C. 2 | D. 5/2 |
Câu 4: Cho hàm số y = x3 - 3x2 + 2. Đồ thị hàm số cắt đường thẳng y = m tại 3 điểm phân biệt
| A. -3 < m < 1 | B. -3 ≦ m ≦ 1 | C. m > 1 | D. m < 3 |
Câu 5: Đường thẳng y = m cắt đồ thị hàm số y = x3 - 3x + 2 tại 3 điểm phân biệt khi
| A. m > 4 | B. 0 ≦ m < 4 | C. 0 < m ≦ 4 | D. 0 < m < 4 |
Câu 6: Đường thẳng y = m không cắt đồ thị hàm số y = -2x4 + 4x2 + 2 khi
| A. 0 < m < 4 | B. m > 4 | C. m < 0 | D. m = 0; m = 4 |
Câu 7: Cho hàm số ![]() có đồ thị (C). Tìm các giá trị của m để đường thẳng d: y = x + m - 1 cắt đồ thị hàm số (C) tại hai điểm phân biệt A, B sao cho AB = 2√3
có đồ thị (C). Tìm các giá trị của m để đường thẳng d: y = x + m - 1 cắt đồ thị hàm số (C) tại hai điểm phân biệt A, B sao cho AB = 2√3
| A. m = 4 ± √10 | B. m = 2 ± √10 | C. m = 4 ± √3 | D. m = 2 ± √3 |
Câu 8: Với giá trị nào của m được liệt kê bên dưới thì đồ thị hàm số y = x4 - 8x2 + 3 cắt đường thẳng y = 4m tại 4 điểm phân biệt:
| A. -13/4 < m < 3/4 | B. -13/4 ≤ m ≤ 3/4 |
| C. m ≤ 3/4 | D. m ≥ -13/4 |
Câu 9: Cho hàm số ![]() có đồ thị (C) và đường thẳng d: y = x + m với giá trị nào của m thì d cắt (C) tại hai điểm phân biệt
có đồ thị (C) và đường thẳng d: y = x + m với giá trị nào của m thì d cắt (C) tại hai điểm phân biệt
| A. m < 2 | B. m > 6 |
| C. 2 < m < 6 | D. m < 2 hoặc m > 6 |
Câu 10: Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
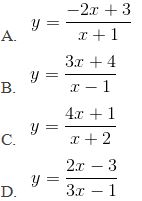
Câu 11: Hoành độ giao điểm của parabol ![]() \((P):y=\frac{1}{4}x^2-2x\) và đường thẳng
\((P):y=\frac{1}{4}x^2-2x\) và đường thẳng ![]() là:
là:
| A. 2 và 6 | B. 1 và 7 | C. 3 và 8 | D. 4 và 5 |
Câu 12: Cho hàm số y = x3 - 6x2 + 9x - 1 có đồ thị (C). Đường thẳng y = 3 cắt (C) tại mấy điểm?
| A. 3 | B. 2 | C. 1 | D. 0 |
Câu 13: Cho hàm số y = (x - 2)(x2 + mx + m2 - 3) có đồ thị (Cm). Với giá trị nào c
ủa m thì (Cm) cắt Ox tại 3 điểm phân biệt?
| A. – 2 < m < 2 | B. – 2 < m < – 1 |
| C. – 1 < m < 2 | D. -2 < m < 2 và m ≠ -1 |
Câu 14: Cho hàm số y = x4 - 5x2 + 4. Với các giá trị nào của m thì đồ thị hàm số cắt đường thẳng d: y = m tại bốn điểm phân biệt
| A. m > -9/4 | B. m < -9/4 |
| C. -9/4 < m < 4 | D. -4 < m < -9/4 |
Câu 15: Đồ thị hàm số 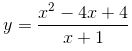 có mấy điểm chung với trục Ox
có mấy điểm chung với trục Ox
| A. 0 | B. 1 | C. 2 | D. 3 |
Câu 16: Đường thẳng d: y = -x + m cắt đồ thị ![]() tại hai điểm phân biệt thì tất cả các giá trị của m là:
tại hai điểm phân biệt thì tất cả các giá trị của m là:
| A. -1 < m < -1/2 | B. -√3 < m < √3 |
| C. m < -√3 hoặc m > √3 | D. m tùy ý |
Câu 17: Với giá trị nào của m thì đồ thị hàm số y = x3 + (m - 1)x + 5 cắt trục hoành tại điểm có hoành độ -2
| A. 1/2 | B. -1/2 |
| C. 15/2 | D. -15/2 |
Câu 18: Xét phương trình x3 + 3x2 = m
A. Với m = 5 thì phương trình có 3 nghiệm
B. Với m = -1 thì phương trình có 2 nghiệm
C. Với m = 4 thì phương trình có 3 nghiệm phân biệt
D. Với m = 2 thì phương trình có 3 nghiệm phân biệt
Câu 19: Số giao điểm của hai đường cong y = x3 - x2 - 2x + 3 và y = x2 - x + 1 là:
| A. 0 | B. 1 | C. 3 | D. 2 |
Câu 20: Các đồ thị của hai hàm số y = 3 - 1/x và y = 4x2 tiếp xúc với nhau tại điểm M có hoành độ là:
| A. x = -1 | B. x = 1 |
| C. x = 2 | D. x = 1/2 |
Câu 21: Đường thẳng d đi qua điểm (1; 3) và có hệ số góc k cắt trục hoành tại điểm A và trục tung tại điểm B (Hoành độ của A và tung độ của B là những số dương). Diện tích tam giác OAB nhỏ nhất khi k bằng
| A. – 11 | B. – 2 | C. – 3 | D. – 4 |
Câu 22: Tìm m để phương trình x3 + 3x2 - 2 = m có 3 nghiệm phân biệt
| A. m < -2 | B. m > 2 |
| C. -2 < m < 2 | D. m = -2 |
Câu 23: Tìm m để phương trình ![]() có nghiệm trên (-∞; 1]
có nghiệm trên (-∞; 1]
| A. m ≥ -2 | B. m > 2 |
| C. m ≤ -2 | D. m < 2 |
Câu 24: Cho hàm số ![]() \(y={{x}^{3}}-3{{x}^{2}}+4\) có đồ thị (C). Gọi d là đường thẳng đi qua
\(y={{x}^{3}}-3{{x}^{2}}+4\) có đồ thị (C). Gọi d là đường thẳng đi qua ![]() \(I\left( 1,2 \right)\) với hệ số góc là k. Tập tất cả các giá trị k để d cắt (C) tại 3 điểm phân biệt I, A, B sao cho I là trung điểm của đoạn AB
\(I\left( 1,2 \right)\) với hệ số góc là k. Tập tất cả các giá trị k để d cắt (C) tại 3 điểm phân biệt I, A, B sao cho I là trung điểm của đoạn AB
Câu 25: Với những giá trị nào của tham số m thì ![]() \(\left( {{C}_{m}} \right):y={{x}^{3}}-3\left( m+1 \right){{x}^{2}}+2\left( {{m}^{2}}+4m+1 \right)x-4m\left( m+1 \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
\(\left( {{C}_{m}} \right):y={{x}^{3}}-3\left( m+1 \right){{x}^{2}}+2\left( {{m}^{2}}+4m+1 \right)x-4m\left( m+1 \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
![]() \(A. \frac{-1}{2}< m,m\ne 1\)
\(A. \frac{-1}{2}< m,m\ne 1\)![]() \(B. m>\frac{1}{2}\)
\(B. m>\frac{1}{2}\)![]() \(C. m\ge \frac{1}{2}\)
\(C. m\ge \frac{1}{2}\)![]() \(D. m\ne 1\)
\(D. m\ne 1\)
Câu 26: Cho đồ thị ![]() \(\left( C \right):y=4{{x}^{3}}-3x+1\) và đường thẳng
\(\left( C \right):y=4{{x}^{3}}-3x+1\) và đường thẳng ![]() \(d:y=m\left( x-1 \right)+2\). Tất cả giá trị tham số m để (C) cắt d tại một điểm?
\(d:y=m\left( x-1 \right)+2\). Tất cả giá trị tham số m để (C) cắt d tại một điểm?
Câu 27: Cho hàm số ![]() \(y=\frac{2x+1}{x+1}\) có đồ thị (C) và đường thẳng
\(y=\frac{2x+1}{x+1}\) có đồ thị (C) và đường thẳng ![]() \(d:y=x+m\). Giá trị nào của tham số m để d cắt (C) tại 2 điểm phân biệt A, B sao cho
\(d:y=x+m\). Giá trị nào của tham số m để d cắt (C) tại 2 điểm phân biệt A, B sao cho ![]() \(AB=\sqrt{10}\) là:
\(AB=\sqrt{10}\) là:
A. m = 6 hoặc m = 0
B. m = 0
C. m = 6![]() \(D. 0\le m\le 6\)
\(D. 0\le m\le 6\)
Câu 28: Cho hàm số ![]() \(y=\frac{2x+1}{x+1}\) có đồ thị (C) và đường thẳng
\(y=\frac{2x+1}{x+1}\) có đồ thị (C) và đường thẳng ![]() \(d:y=x+m\). Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho tiếp tuyến tại A và B song song với nhau
\(d:y=x+m\). Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho tiếp tuyến tại A và B song song với nhau
Câu 29: Cho ![]() \((P):y={{x}^{2}}-2x-{{m}^{2}}\) và
\((P):y={{x}^{2}}-2x-{{m}^{2}}\) và ![]() \(d:y=x+m\). Giả sử (P) cắt d tại hai điểm phân biệt A, B thì tọa độ trung điểm I của đoạn thẳng AB là:
\(d:y=x+m\). Giả sử (P) cắt d tại hai điểm phân biệt A, B thì tọa độ trung điểm I của đoạn thẳng AB là:
Câu 30: Giá trị nào của tham số m để đồ thị hàm số ![]() \(\left( {{C}_{m}} \right):y=\left( m-1 \right){{x}^{3}}+{{x}^{2}}-m\) chỉ có một điểm chung với trục hoành?
\(\left( {{C}_{m}} \right):y=\left( m-1 \right){{x}^{3}}+{{x}^{2}}-m\) chỉ có một điểm chung với trục hoành?
![]() \(A. m=1\)
\(A. m=1\)![]() \(B. m<0\) hoặc
\(B. m<0\) hoặc ![]() \(m>\frac{4}{3}\)
\(m>\frac{4}{3}\)![]() \(C. m<0\)
\(C. m<0\)![]() \(D. m>\frac{4}{3}\)
\(D. m>\frac{4}{3}\)
Câu 31: Cho hàm số ![]() \(y=\frac{2x+1}{x-1}\) có đồ thị (C) và đường thẳng
\(y=\frac{2x+1}{x-1}\) có đồ thị (C) và đường thẳng ![]() \(d:y=x+m\). Đường thẳng (d) cắt đồ thị hàm số (C) tại hai điểm A và B. Với
\(d:y=x+m\). Đường thẳng (d) cắt đồ thị hàm số (C) tại hai điểm A và B. Với ![]() \(C\left( -2,5 \right)\), giá trị của tham số m để tam giác ABC đều là:
\(C\left( -2,5 \right)\), giá trị của tham số m để tam giác ABC đều là:
![]() \(A. m=1\)
\(A. m=1\)![]() \(B. m=1\) hoặc
\(B. m=1\) hoặc ![]() \(m=5\)
\(m=5\)![]() \(C. m=5\)
\(C. m=5\)![]() \(D. m=-5\)
\(D. m=-5\)
Câu 32: Cho hàm số ![]() \(y={{x}^{4}}-\left( 2m-1 \right){{x}^{2}}+2m\) có đồ thị (C). Tất cả các giá trị của tham số m để đường thẳng
\(y={{x}^{4}}-\left( 2m-1 \right){{x}^{2}}+2m\) có đồ thị (C). Tất cả các giá trị của tham số m để đường thẳng ![]() \(d:y=2\) cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là:
\(d:y=2\) cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là:
 \(C. \left\{ \begin{matrix}
m\ne \dfrac{3}{2} \\
1< m<2 \\
\end{matrix} \right.\) \(C. \left\{ \begin{matrix}
m\ne \dfrac{3}{2} \\
1< m<2 \\
\end{matrix} \right.\) |
 \(D. \left\{ \begin{matrix}
m\ne \dfrac{3}{2} \\
1< m<\dfrac{11}{2} \\
\end{matrix} \right.\) \(D. \left\{ \begin{matrix}
m\ne \dfrac{3}{2} \\
1< m<\dfrac{11}{2} \\
\end{matrix} \right.\) |
Đáp án bài tập trắc nghiệm sự tương giao giữa hai đồ thị
| 1.C | 2.D | 3.C | 4.A | 5.D | 6.B | 7.A | 8.A |
| 9.D | 10.B | 11.C | 12.B | 13.D | 14.C | 15.B | 16.D |
| 17.B | 18.D | 19.C | 20.D | 21.C | 22.C | 23.A | 24.D |
| 25.A | 26.D | 27.A | 28.A | 29.D | 30.B | 31.C | 32.B |



