Đề khảo sát Toán 12 năm 2025 trường THPT Tĩnh Gia 1, Thanh Hóa
Khảo sát chất lượng Toán 12
Lớp:
Lớp 12
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Mã đề 1201 Trang 1/4
SỞ GD&ĐT THANH HÓA
TRƯỜNG THPT TĨNH GIA 1
--------------------
(Đề thi có 04 trang)
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12
NĂM HỌC 2024 - 2025
MÔN: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên: ............................................................................
Số báo danh: .......
Mã đề 1201
PHẦN I. Trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
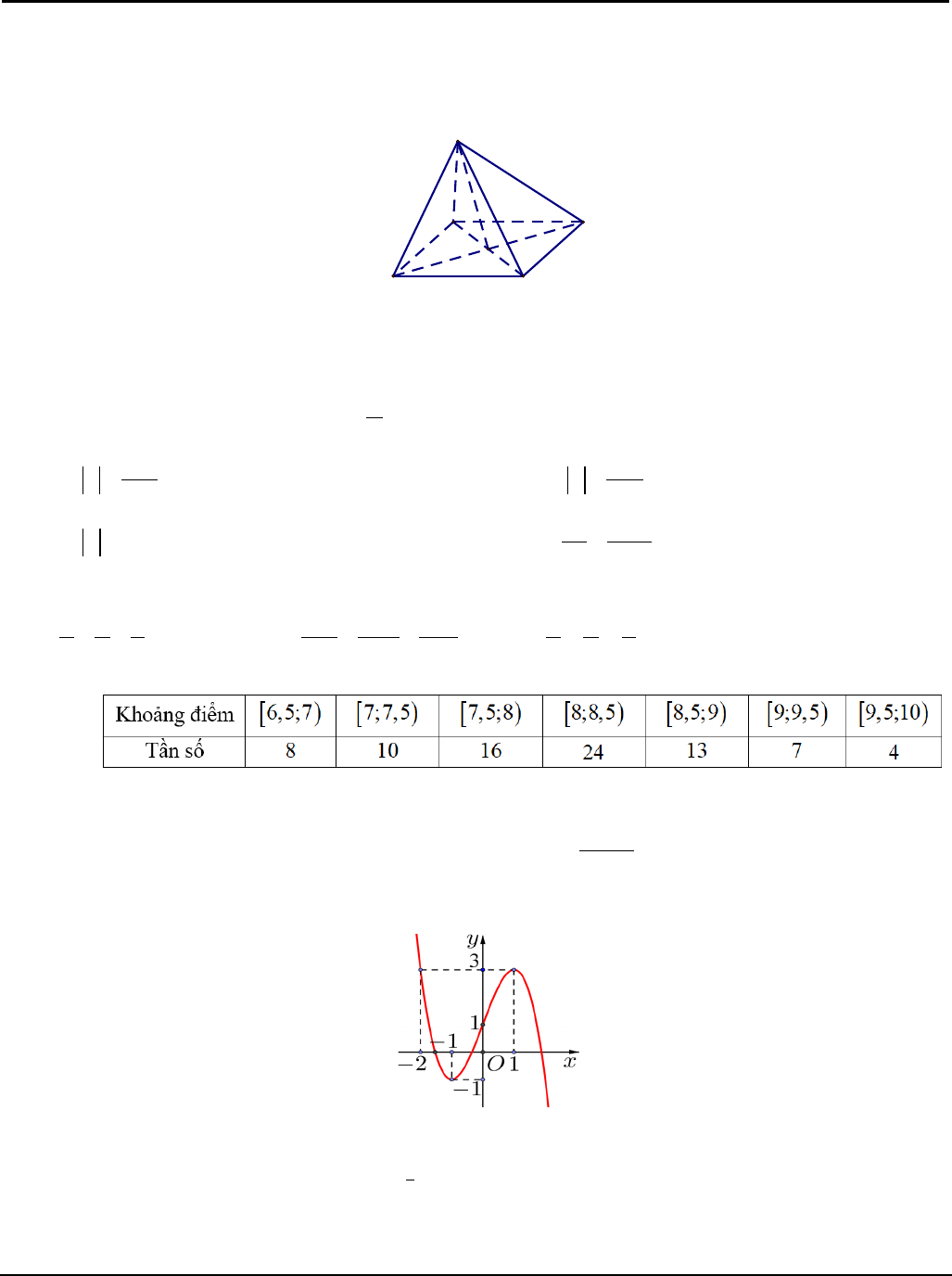
Câu 1. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
(hình vẽ bên).
Phát biểu nào sau đây là đúng?
A.
SA SB SC SD−=−
. B.
SA SB SC SD+=+
.
C.
SA SC SB SD−=−
. D.
SA SC SB SD+=+
.
Câu 2. Nguyên hàm của hàm số
=+−
1
( ) 2 3sin
x
fx x
x
là
A.
++ +
2
ln 3cos
ln 2
x
x xC
. B.
+− +
2
ln 3cos
ln 2
x
x xC
.
C.
+−+ln 2 ln 2 3cos
x
x xC
. D.
+
−+ − +
+
1
2
12
3cos
1
x
xC
xx
.
Câu 3. Trong không gian tọa độ
Oxyz
cho điểm
( )
1; 2; 3M
, phương trình đường thẳng
OM
là
A.
1
123
xyz
++=
. B.
123
149
xy z−−−
= =
. C.
123
xyz
= =
. D.
23xyz= =
.
Câu 4. Thống kê điểm trung bình môn Toán của một số học sinh lớp 12 được mẫu số liệu sau:
Phương sai của mẫu số liệu về điểm trung bình môn Toán của các học sinh đó là
A. 0,785. B. 0,78. C. 0,609. D. 0,616.
Câu 5. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
23
1
x
y
x
−
=
+
lần lượt có phương trình là
A.
1, 2xy= =
. B.
1, 3xy=−=−
. C.
1, 2xy=−=
. D.
2, 1xy= = −
.
Câu 6. Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
( )
1; +∞
B.
( )
1;1−
. C.
( )
;1−∞ −
. D.
( )
;1−∞
.
Câu 7. Tập nghiệm của bất phương trình
( )
1
2
log 3 1 1
x
− >−
là:
A.
( )
1; +∞
. B.
( )
0; 2
. C.
( )
0;1
. D.
( )
;1−∞
.
O
D
S
A
B
C
Mã đề 1201 Trang 2/4
Câu 8. Trong không gian tọa độ
Oxyz
, mặt phẳng
(
)
P
đi qua
( )
1; 2; 3M
và song song với mặt phẳng
(
)
Oxy
có phương trình là
A.
2y =
. B.
2 50xy+ −=
. C.
3z =
. D.
1x =
.
Câu 9. Cho cấp số nhân
( )
n
u
có
1
2u =
và
2
1u =
. Số hạng
10
u
là:
A.
1
512
. B.
1
256
. C.
1024
. D.
512
.
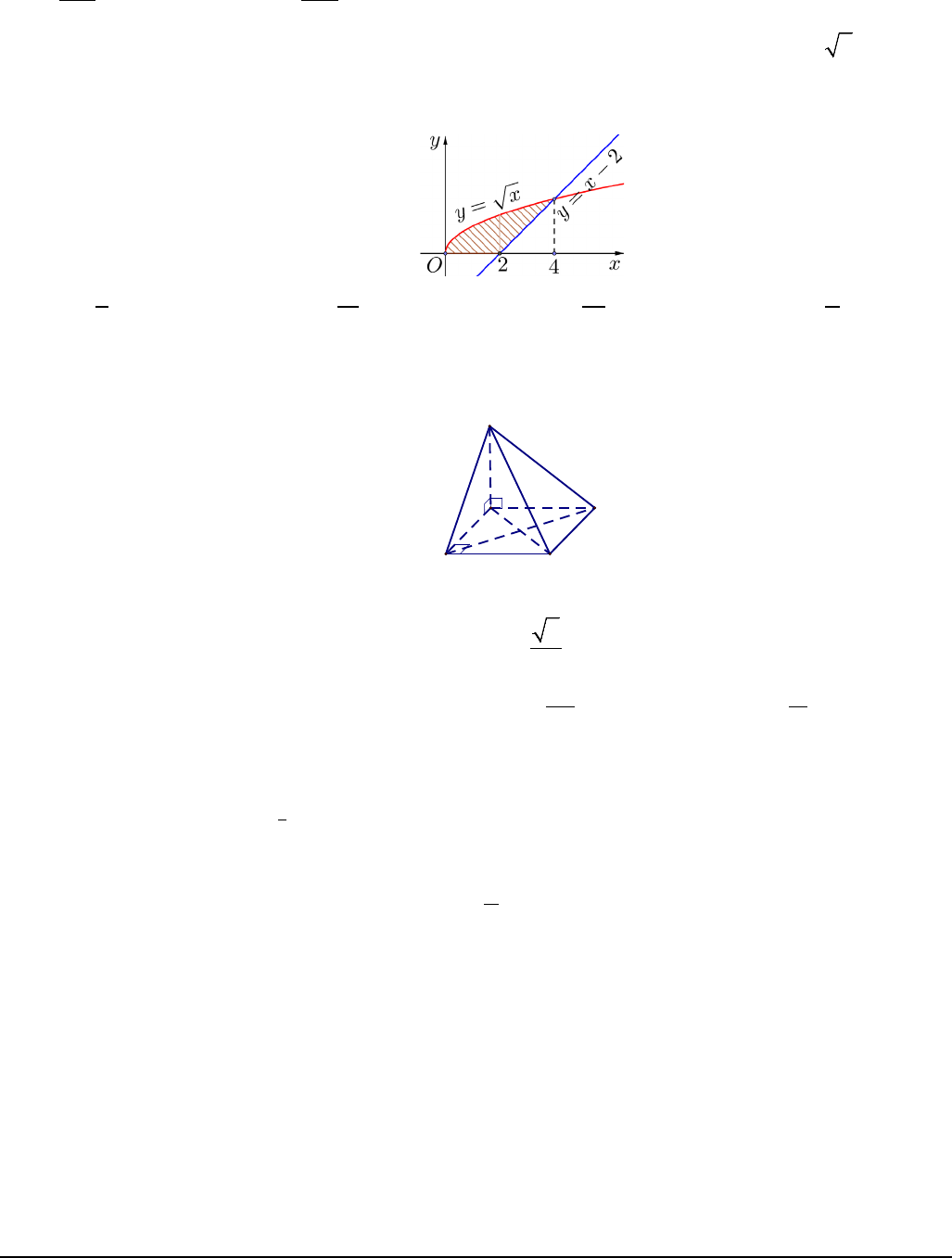
Câu 10. Trong mặt phẳng tọa độ
,Oxy
cho hình phẳng
( )
H
giới hạn bởi đồ thị hàm số
yx=
, trục
hoành và đường thẳng
2yx
= −
được minh họa là phần gạch sọc như hình vẽ. Diện tích
S
của hình
phẳng
( )
H
là
A.
8
3
S =
B.
11
3
S =
C.
10
3
S =
D.
7
3
S =
Câu 11. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông,
( )
SA ABCD
⊥
(hình vẽ bên). Khẳng
định nào sau đây là sai.
A.
(
) ( )
SAC SBD
⊥
. B.
( ) ( )
SAC ABCD⊥
. C.
(
) ( )
SBC SAB⊥
. D.
( ) ( )
SBC SCD⊥
.
Câu 12. Tổng tất cả các nghiệm của phương trình
2
sin 2
2
x =
trên
[ ]
0; 2
π
là:
A.
2
π
. B.
3
π
. C.
5
2
π
. D.
4
π
.
PHẦN II. Trắc nghiệm đúng – sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý (a), (b), (c), (d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
( )
( )
1
2
log 3 4fx x= +
.
a) Giá trị lớn nhất của
( )
fx
trên nửa khoảng
[
)
2; +∞
bằng
2
1 log 5−−
.
b) Tập nghiệm của bất phương trình
( )
2
7
2
2
fx x x<− + −
là
( )
0; 4
.
c) Tập xác định của hàm số là
( )
0;D = +∞
.
d) Hàm số
(
)
fx
nghịch biến trên khoảng
( )
0; +∞
Câu 2. Cây đậu Hà Lan khi trồng có chiều cao 3 centimet. Gọi
( )
ht
là độ cao tính bằng centimet của cây
đậu Hà Lan tại thời điểm
t
kể từ khi được trồng, với
t
tính theo tuần. Khảo sát cho thấy tốc độ tăng chiều
cao của cây đậu Hà Lan sau khi trồng là
( )
32
0, 02 0,3ht t t
′
=−+
(centimet/tuần).
a) Vào thời điểm cây đậu Hà Lan đó phát triển nhanh nhất thì chiều cao của cây là 53 centimet.
b) Hàm số
( )
ht
có công thức
( )
43
0, 005 0,1ht t t=−+
.
c) Chiều cao tối đa của cây đậu Hà Lan đó là 88 centimet.
d) Giai đoạn tăng trưởng của cây đậu Hà Lan đó kéo dài 15 tuần.
D
S
A
B
C
Mã đề 1201 Trang 3/4
Câu 3. Một nhà mạng viễn thông đang triển khai hệ thống phát hiện và chặn các số điện thoại thực hiện
cuộc gọi lừa đảo. Tuy nhiên, do hệ thống chưa hoàn hảo, nó có thể chặn nhầm một số điện thoại hợp lệ
hoặc bỏ sót một số điện thoại lừa đảo. Hệ thống hoạt động với các thông số sau:
+ Tỷ lệ số điện thoại lừa đảo trong hệ thống là
5%
(tức là
5%
tổng số thuê bao là số lừa đảo).
+ Xác suất hệ thống phát hiện đúng và chặn một số điện thoại lừa đảo là
94%
.
+ Xác suất hệ thống chặn nhầm một số điện thoại hợp lệ (tức là số điện thoại không lừa đảo) là
3%
.
Chọn ngẫu nhiên một số điện thoại đã được thử nghiệm hệ thống.
a) Biết rằng một số điện thoại không bị chặn, xác suất để số điện thoại đó là số hợp lệ bằng
1813
1849
.
b) Biết rằng một số điện thoại bị chặn, xác suất để số điện thoại đó là số lừa đảo bằng
90
151
.
c) Biết rằng số điện thoại đó là số lừa đảo, xác suất để số điện thoại đó bị chặn là 0.94.
d) Xác suất để một số điện thoại bất kỳ bị chặn là
151
2000
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho
( )
( ) ( )
0;1;1 , 1; 0; 3 , 1; 2; 3AB C− −−−
và mặt cầu
( )
S
có
phương trình
2 22
2 2 20xyz xz+ + − + −=
. Xét tính đúng sai của các khẳng định sau:
a) Mặt phẳng
( )
ABC
cắt mặt cầu
( )
S
theo một đường tròn có bán kính bằng
42
3
.
b) Mặt phẳng
( )
ABC
có phương trình
2 2 10x yz− + −=
.
c) Điểm
( )
;;D abc
thuộc mặt cầu
( )
S
sao cho thể tích tứ diện
ABCD
lớn nhất. Khi đó
2
3
abc++=
.
d) Mặt cầu
( )
S
có bán kính
2R =
.
PHẦN III. Trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
1, 2AB cm AC cm= =
;
90SBA SCA= = °
, góc giữa
BC
và mặt phẳng
( )
SAB
bằng
45°
. Tính khoảng cách giữa hai đường thẳng
SA
và
BC
, với đơn vị là
cm
(centimet) và kết quả làm tròn đến hàng phần trăm.
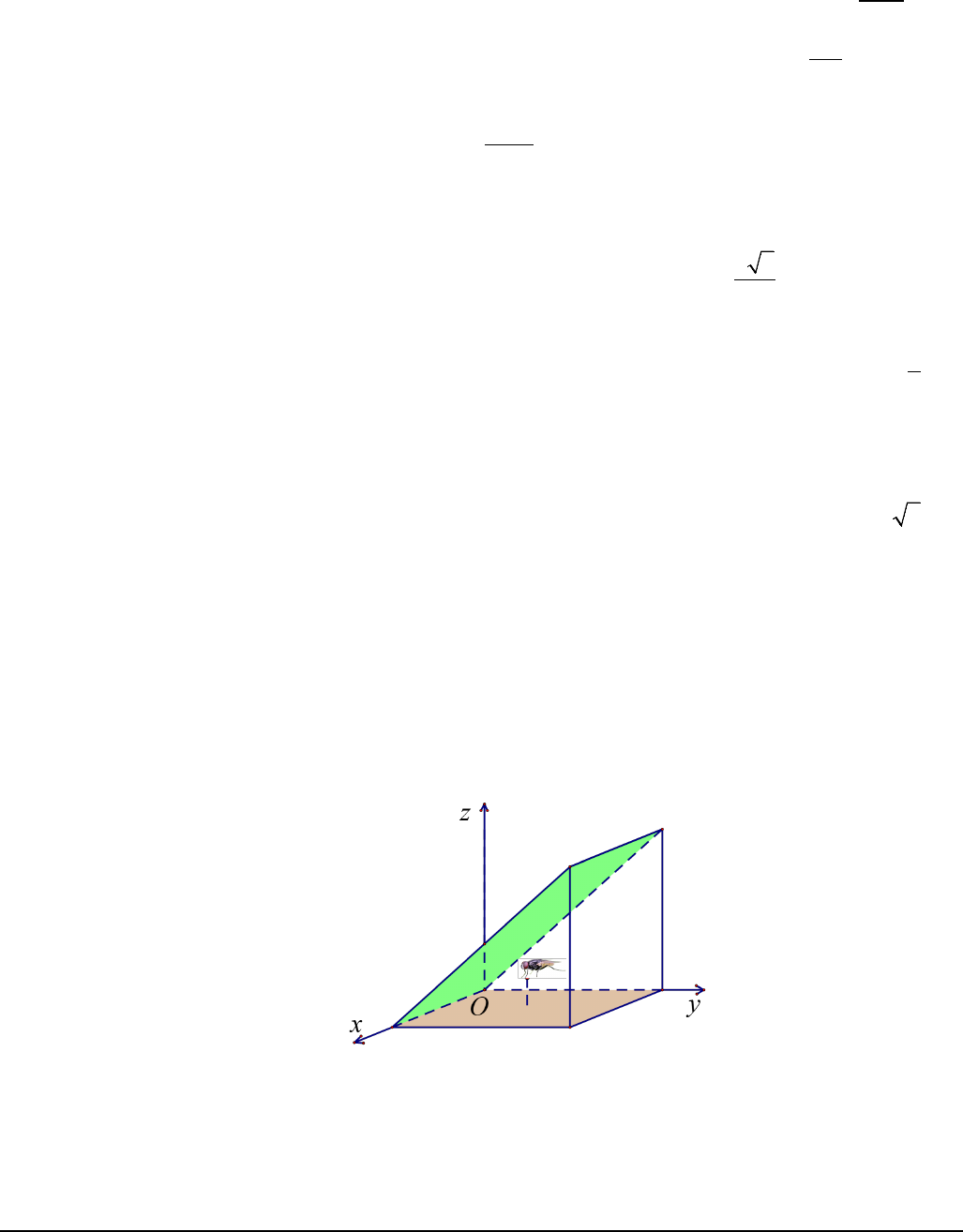
Câu 2. Trong không gian
Oxyz
với đơn vị dài trên mỗi trục là
1cm
, một con ruồi xuất phát tại vị trí điểm
( )
321A ;;
bay xuống mặt phẳng
(
)
Oxy
nó nghỉ tại chỗ một lát rồi sau đó bay đến mặt phẳng
( )
:0P yz−=
. Tại mặt phẳng
(
)
P
con ruồi cẩn thận bò đi một đoạn đường thẳng có độ dài bằng
2cm
,
sau đó nó bay trở về vị trí xuất phát. Tính độ dài ngắn nhất của quãng đường mà con ruồi đã thực hiện
(Kết quả tính theo đơn vị
cm
và làm tròn đến hàng phần trăm).
Câu 3. Bác Hai có một mảnh đất rộng 6 ha. Bác dự tính trồng cà chua và bắp cho mùa vụ sắp tới. Nếu
trồng bắp thì bác Hai cần mười ngày để trồng một ha. Nếu trồng cà chua thì bác Hai cần hai mươi ngày để
trồng một ha. Biết rằng mỗi ha bắp sau thu hoạch bán được 30 triệu đồng, mỗi ha cà chua sau thu hoạch
bán được 50 triệu đồng và bác Hai chỉ còn 100 ngày để canh tác cho kịp mùa vụ. Số tiền nhiều nhất mà
bác Hai có thể thu được sau mùa vụ này là bao nhiêu triệu đồng.
Đề khảo sát chất lượng Toán 12 năm 2025 trường Tĩnh Gia 1, Thanh Hóa
VnDoc.com xin gửi tới bạn đọc bài viết Đề khảo sát Toán 12 năm 2025 trường THPT Tĩnh Gia 1, Thanh Hóa có đáp án để bạn đọc cùng tham khảo. Đề thi được biên soạn theo cấu trúc đề thi mới. Đề gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trả lời ngắn. Thí sinh làm đề trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây để có thêm tài liệu ôn thi khảo sát chất lượng lớp 12 nhé


