Đề khảo sát Toán 12 năm 2025 lần 2 Sở GD&ĐT Phú Thọ
Khảo sát chất lượng Toán 12
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12 THPT LẦN 2
PHÚ THỌ NĂM HỌC 2024 - 2025
ĐỀ CHÍNH THỨC MÔN: TOÁN
(Đề thi có 04 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:.................................................... Số báo danh:........................... Mã đề thi 1020
Phần I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trong không gian Oxyz, cho mặt cầu (S) có phương trình: (x − 2)
2
+ (y + 1)
2
+ (z − 3)
2
= 9. Tọa
độ tâm của mặt cầu đã cho là
A. (2; −1; 3). B. (−2; 1; 3). C. (−2; 1; −3). D. (−2; −1; 3).
Câu 2. Họ các nguyên hàm của hàm số f (x) = 2
x
là
A.
2
x
ln 2
+ C. B. 2
x
ln 2 + C. C. x ·2
x−1
+ C. D. 2
x
ln x + C.
Câu 3. Cho hàm số y =
ax + b
cx + d
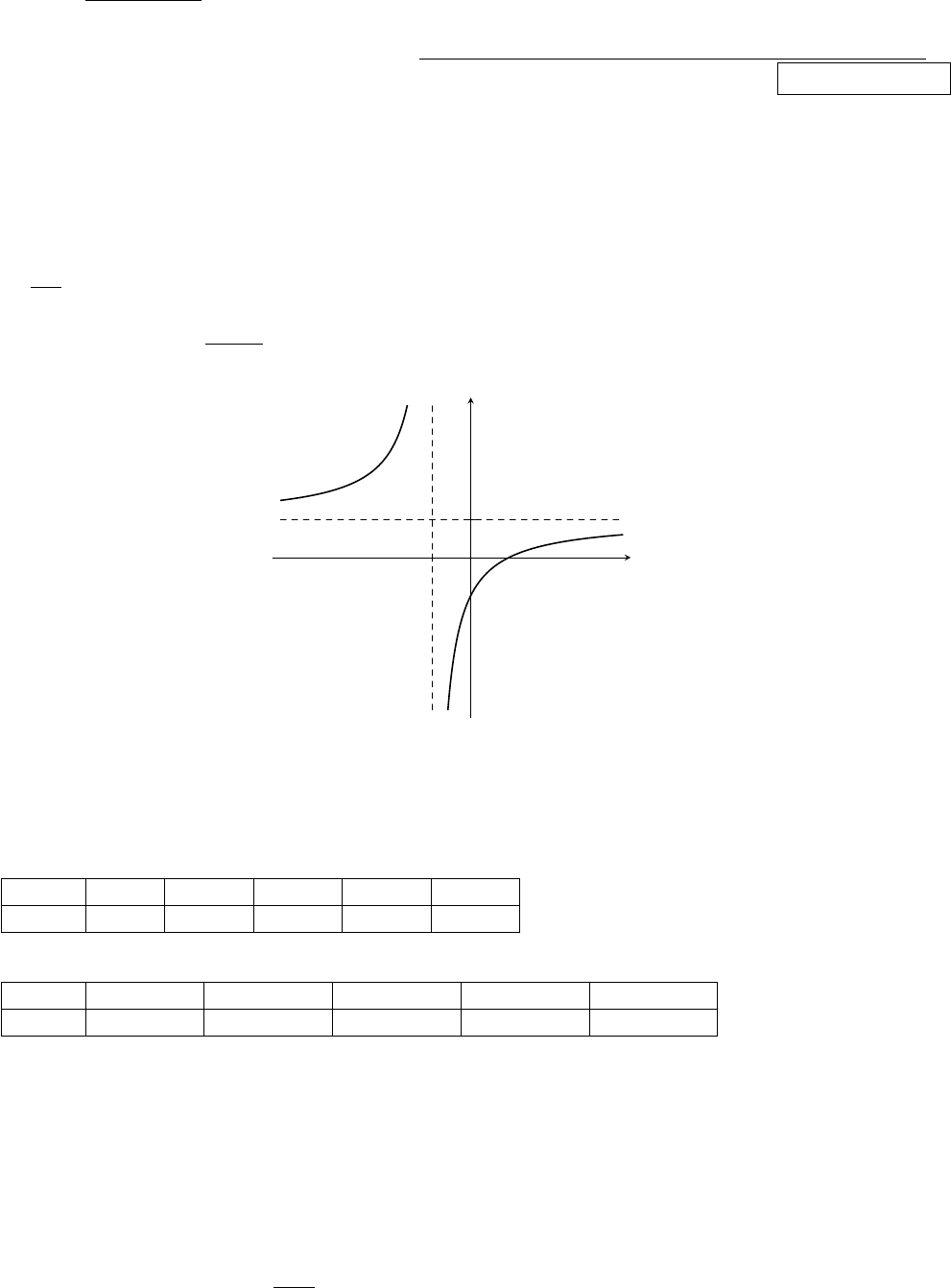
(a, b, c, d ∈ R) có đồ thị là đường cong như hình vẽ.
x
y
O
−1
1
Tọa độ tâm đối xứng của đồ thị hàm số đã cho là
A. (−1; 1). B. (1; 1). C. (1; −1). D. (0; 1).
Câu 4. Hai mẫu số liệu ghép nhóm A, B có bảng tần số ghép nhóm như sau:
Nhóm A
Nhóm [0; 10) [10; 20) [20; 30) [30; 40) [40; 50)
Tần số 8 9 5 6 2
Nhóm B
Nhóm [0, 3; 10, 3) [10, 3; 20, 3) [20, 3; 30, 3) [30, 3; 40, 3) [40, 3; 50, 3)
Tần số 16 18 10 12 4
Gọi ∆
Q
A
, ∆
Q
B
lần lượt là khoảng tứ phân vị của mẫu số liệu ghép nhóm A, B. Phát biểu nào sau đây
đúng?
A. ∆
Q
B
= 2∆
Q
A
. B. ∆
Q
B
= 0, 3 + ∆
Q
A
. C. ∆
Q
B
= ∆
Q
A
. D. ∆
Q
B
= 0, 3∆
Q
A
.
Câu 5. Số nghiệm của phương trình log(2x − 1) = log(x
2
− 4) là
A. 2. B. 0. C. 1. D. 3.
Câu 6. Nếu
b
Z
a
f(x) dx = 2025 thì
b
Z
a
2f(x) dx bằng
A. 2025
2
. B.
2025
2
. C. 2023. D. 4050.
Câu 7. Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ.
1

x
y
O
−2
2
−2
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (−∞; −2). B. (−2; 0). C. (0; +∞). D. (−1; 1).
Câu 8. Cho cấp số nhân (u
n
) có u
1
= 1, u
4
= 27. Công bội q của cấp số nhân đã cho bằng
A.
26
3
. B. ±3. C. −3. D. 3.
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng đáy. Đường
thẳng CD vuông góc với mặt phẳng nào dưới đây?
A. (SAC). B. (SAD). C. (SAB). D. (SBC).
Câu 10. Cho tứ diện S.ABC với M , N , P lần lượt là trung điểm của SA, SB, SC (tham khảo hình vẽ).
Khẳng định nào sau đây đúng?
A.
−−→
AB =
1
2
(
−−→
P N −
−−→
P M ). B.
−−→
AB =
−−→
P N −
−−→
P M .
C.
−−→
AB = 2(
−−→
P M −
−−→
P N ). D.
−−→
AB = 2(
−−→
P N −
−−→
P M ).
Câu 11. Tập nghiệm của phương trình (0, 2)
x
≤ 4 là
A. (−∞; log
4
0, 2]. B.
log
0,2
4; +∞
. C.
−∞; log
0,2
4
. D. [log
4
0, 2; +∞).
Câu 12. Trong không gian Oxyz, cho mặt phẳng (P ) có phương trình: 2x − y + z − 4 = 0. Phương trình
mặt phẳng (Q) song song với (P ) và đi qua điểm M (1; −1; 3) là
A. 2x − y + z + 6 = 0. B. 2x + 3y − z + 4 = 0.
C. 2x − y + z − 6 = 0. D. x − y + 3z − 6 = 0.
Phần II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh
chọn đúng hoặc sai.
Câu 1. Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được
cho bởi hàm số v(t) = −0, 1t
3
+ t
2
, trong đó t tính theo tuần, v(t) tính bằng cm/tuần. Gọi h(t) (tính bằng
cm) là độ cao của cây cà chua ở tuần thứ t (Nguồn: A. Bigalke et al., Grundkurs ma-1, Cornelsen 2016).
a) h
′
(t) = v(t).
b) h(t) = −
t
4
40
+
t
3
3
+ 5, t ≥ 0.
c) Giai đoạn tăng chiều cao của cây cà chua kéo dài 9 tuần.
d) Chiều cao tối đa của cây cà chua (kết quả làm tròn đến hàng phần chục) bằng 88, 3 cm.
Câu 2. Cho hàm số f (x) = 2 sin x +
√
3x.
2

a) f(0) = 0, f (π) =
√
3π.
b) Đạo hàm của hàm số đã cho là f
′
(x) = −2 cos x +
√
3.
c) Nghiệm của phương trình f
′
(x) = 0 trên đoạn [0; π] là x =
π
6
.
d) Giá trị lớn nhất của hàm số f (x) trên đoạn [0; π] bằng 1 +
5
√
3π
6
.
Câu 3. Đường ống dẫn dầu trên không là hệ thống đường ống được treo trên các giá đỡ hoặc cột cao,
dùng để vận chuyển dầu thô hoặc các sản phẩm dầu mỏ từ nơi này đến nơi khác mà không cần chôn dưới
lòng đất. Hệ thống này thường được sử dụng trong các khu vực có địa hình khó khăn, vùng băng giá, rừng
rậm..., những nơi mà việc đào đường ống ngầm không khả thi.
Với hệ trục tọa độ Oxyz thích hợp, mặt đất là mặt phẳng (Oxy), đơn vị trên mỗi trục là mét, người ta thiết
lập một đường ống dẫn dầu trên không dọc theo đường thẳng d :
x = 0
y = t
z = 20
(t là tham số).
Vì địa hình phức tạp, người ta chọn điểm A(15; 10; 15) để làm điểm trung chuyển dầu từ mặt đất đến đường
ống này.
a) Đường thẳng d nằm trên mặt phẳng (Oyz).
b) Điểm đối xứng với A qua mặt phẳng (Oxy) có tọa độ A
′
(−15; −10; 15).
c) Do thực tế công việc, người ta cần xác định vị trí điểm B(0; b; 20) thuộc đường ống và vị trí điểm
C(m; n; 0) thuộc mặt đất sao cho tổng độ dài các đoạn đường AB, BC, AC nhỏ nhất. Ta có m+n+b =
200
7
.
d) Giá trị nhỏ nhất của tổng độ dài các đoạn đường AB, BC, AC làm tròn đến hàng phần chục bằng
45, 5 m.
Câu 4. Giả sử có một đồng xu cân bằng (fair coin) và một đồng xu thiên lệch (biased coin) mà mặt ngửa
(heads) xuất hiện với xác suất
3
4
. Một người chơi chọn ngẫu nhiên một trong hai đồng xu và tung nó ba
lần. Gọi A là biến cố: “Người chơi chọn đồng xu cân bằng”; B là biến cố: “Ba lần tung đồng xu đều xuất
hiện mặt ngửa”.
a) P (A) =
1
2
.
b) P (B | A) =
3
8
.
c) Xác suất người đó chọn được đồng xu cân bằng biết rằng kết quả ba lần tung đồng xu đều xuất hiện
mặt ngửa là 0, 25 (kết quả làm tròn đến hàng phần trăm).
d) Biết rằng đồng xu được chọn tung ba lần đều xuất hiện mặt ngửa, xác suất người chơi đó tung lần
thứ tư tiếp tục xuất hiện mặt ngửa là 0, 69 (kết quả làm tròn đến hàng phần trăm).
3
Đề khảo sát chất lượng Toán 12 năm 2025 lần 2 Sở Phú Thọ
Đề thi khảo sát Toán 12 năm 2025 lần 2 Sở GD&ĐT Phú Thọ là tài liệu hữu ích giúp bạn đọc có thể trau dồi, luyện tập nội dung kiến thức, chuẩn bị cho kì thi sắp tới nhé. Đề gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trả lời ngắn. Thí sinh làm đề trong thời gian 90 phút. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây để có thêm tài liệu ôn thi và khảo sát chất lượng lớp 12 nhé.


