Toán 12 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Toán 12 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, VnDoc xin mời các bạn tham khảo tài liệu Toán 12 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số. Bộ tài liệu hướng dẫn chi tiết cách lập bảng biến thiên, xác định và cách vẽ đồ thị hàm số bậc nhất, hàm số bậc hai, hàm số bậc 3, ... được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và đề thi THPT Quốc gia. Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.
- Tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác
- 300 câu hỏi trắc nghiệm môn Toán lớp 12 (Có đáp án)
- Bài tập trắc nghiệm cực trị của hàm số và điểm uốn (Có đáp án)
- Bài tập trắc nghiệm tính đơn điệu của hàm số
- Câu hỏi trắc nghiệm môn Toán lớp 12: Cực trị của hàm số
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 12, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 12 sau: Nhóm Tài liệu học tập lớp 12. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
A. Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị hàm số
1. Khảo sát sự biến thiên
Bước 1: Tìm tập xác định của hàm số. Xét tính chẵn lẻ, tuần hoàn của hàm số để thu hẹp phạm vi khảo sát.
Bước 2: Khảo sát và lập bảng biến thiên:
- Xét sự biến thiên của hàm số
+ Tìm đạo hàm bậc nhất y’
+ Tìm các điểm tai đó y’ bằng 0 xác định
+ Xét dấu y’ và suy ra chiều biến thiên của hàm số
- Tìm cực trị
- Tìm giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có)
Bước 3: Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị
2. Cách vẽ đồ thị hàm số
- Vẽ các đường tiệm cận của đồ thị (nếu có)
- Tìm giao điểm của đồ thị với Ox, Oy
- Vẽ các điểm đặc biệt: cực trị, điểm uốn
- Tìm thêm điểm thuộc đồ thị hàm số (càng nhiều điểm đồ thị càng chính xác)
- Nêu tính chất đối xứng của đồ thị: trục đối xứng, tâm đối xứng.
3. Khảo sát hàm đa thức bậc 3: 
\(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\)
Ta có: \(y'=3a{{x}^{2}}+2bx+c,\Delta '={{b}^{2}}-3ac\)
- Hàm số có hai cực trị nếu \(\Delta '>0\) và không có cực trị nếu \(\Delta '\le 0\)
\(y''=6ax+2b,y''=0\Leftrightarrow x=\frac{-b}{2a}\) là hoành độ điểm uốn, đồ thị nhận điểm uốn làm tâm đối xứng
Dạng đồ thị hàm số bậc 3
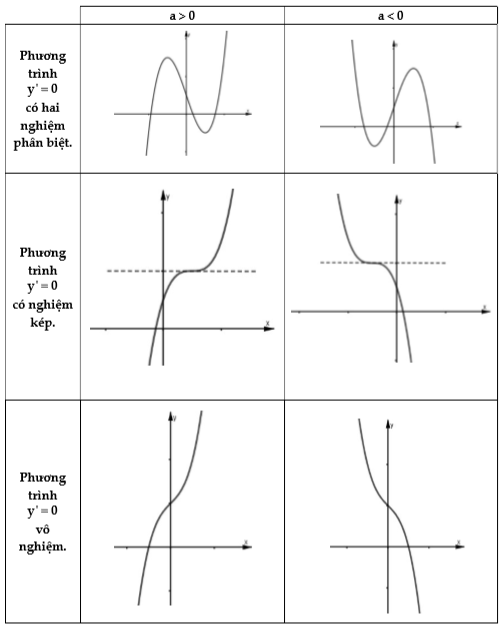
4. Khảo sát hàm đa thức bậc bốn trùng phương: \(y=a{{x}^{4}}+b{{x}^{2}}+c\)
\(y'=4a{{x}^{3}}+2bx=2x\left( 2a{{x}^{2}}+b \right)\Rightarrow y'=0\Leftrightarrow \left[ \begin{matrix}
x=0 \\
{{x}^{2}}=\dfrac{-b}{2a} \\
\end{matrix} \right.\)
+ Nếu \(ab\ge 0\) thì hàm số có một cực trị \({{x}_{0}}=0\)
+ Nếu \(ab<0\) thì hàm số có 3 cực trị \({{x}_{0}}=0,{{x}_{1}}=\sqrt{\frac{-b}{2a}},{{x}_{2}}=-\sqrt{\frac{-b}{2a}}\)
- Đồ thị hàm số cắt trục tung tại điểm có tung độ c, cắt trục hoành tại tối đa 4 điểm và các điểm này đối xứng lẫn nhau qua gốc tọa độ O.
- Đồ thị nhận trục Oy làm trục đối xứng.
- Dạng đồ thị hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\)
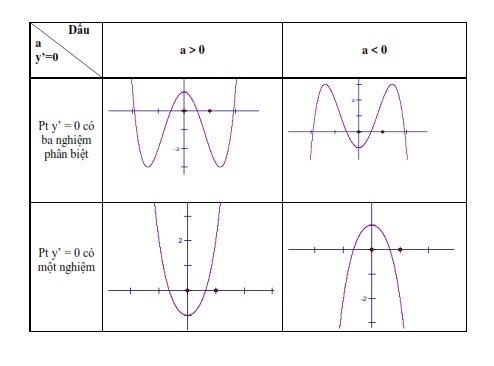
5. Khảo sát hàm phân thức \(y=\frac{ax+b}{cx+d}\)
Điều kiện \(ad-bc\ne 0,c\ne 0\)
Đạo hàm \(y'=\frac{ad-bc}{{{\left( cx+d \right)}^{2}}}\)
+ Nếu \(ad-bc>0\) hàm số đồng biến trên từng khoảng xác định. Đồ thị nằm góc phần tư thứ (II) và thứ (IV) của hai tiệm cận.
+ Nếu \(ad-bc<0\) hàm số nghịch biến trên từng khoảng xác định. Đồ thị nằm góc phần tư thứ (I) và thứ (Iii) của hai tiệm cận.
+ Tiệm cận đứng \(x=-\frac{d}{c}\), tiệm cận ngang \(y=\frac{a}{c}\)
- Đồ thị hàm số có tâm đối xứng \(I\left( \frac{-d}{c},\frac{a}{c} \right)\)
- Đồ thị cắt trục hoành tại điểm có hoành độ \(\frac{-b}{a}\), cắt trục tung tại điểm có tung độ \(\frac{b}{d}\)
B. Giải SGK Toán 12 Bài 5
Trong Sách giáo khoa Toán lớp 12, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 12. Mời các bạn học sinh tham khảo:
C. Giải SBT Toán 12 Bài 5
Sách bài tập Toán 12 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:
D. Bài tập Khảo sát sự biến thiên và vẽ đồ thị hàm số
Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của bài Hàm số này, VnDoc xin gửi tới các bạn học sinh Tài liệu Khảo sát sự biến thiên và vẽ đồ thị hàm số do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:
- Bài tập trắc nghiệm sự tương giao giữa hai đồ thị (Có đáp án)
- Trắc nghiệm Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số
------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Toán 12 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số.Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Thi THPT Quốc gia môn Toán, Thi THPT Quốc gia môn Văn, Thi THPT Quốc gia môn Lịch sử mà VnDoc tổng hợp và đăng tải.
