Trắc nghiệm Toán 12 chương 1: Đường tiệm cận
Toán 12 chương 1: Đường tiệm cận
VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Trắc nghiệm Toán 12 chương 1: Đường tiệm cận, tài liệu kèm theo đáp án và lời giải chi tiết sẽ giúp các bạn học sinh giải bài tập Toán 12 hiệu quả hơn. VnDoc.com mời các bạn học sinh và thầy cô tham khảo chi tiết tại đây nhé.
- Trắc nghiệm Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
- Lý thuyết Toán 12 chương 1: Cực trị của hàm số
- Lý thuyết Toán 12 chương 1: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Trắc nghiệm Toán 12 chương 1: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Lý thuyết Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số
- Trắc nghiệm Toán 12 chương 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Trắc nghiệm Toán 12 chương 1: Đường tiệm cận vừa được VnDoc.com sưu tập và xin gửi tới bạn đọc cùng tham khảo. Bài viết được tổng hợp gồm có 16 câu hỏi trắc nghiệm về chương 1 môn Toán lớp 12 về Đường tiệm cận. Bài tập có đáp án lời giải chi tiết kèm theo. Qua bài viết bạn đọc có thể tính được số đường tiệm cận của đồ thị hàm số, tính tiệm cận ngang, tìm các giá trị thực của tham số... Mời các bạn cùng tham khảo chi tiết và tải về tại đây nhé.
Trắc nghiệm Toán 12 chương 1: Đường tiệm cận
Câu 1: Đồ thị hàm số 
\(y\ =\ \frac{4x-3}{2x^2-x-1}\) có bao nhiêu đường tiệm cận?
A.1
B. 2
C.3
D.4
Câu 2: Tìm mệnh đề sai trong các mệnh đề sau:
A. Đồ thị hàm số \(y\ =\ \frac{2x-1}{x+2}\) có một tiệm cận đứng và một tiệm cận ngang.
B. Đồ thị hàm số \(y\ =\ \frac{2}{x-1}\) có một tiệm cận đứng và không có tiệm cận ngang
C. Đồ thị hàm số \(y\ =\ \frac{4x}{x-3}\) có tiệm cận đứng x = 3 và tiệm cận ngang
D. Đồ thị hàm số \(y\ =\ \frac{m+x}{x-1}\) có một tiệm cận đứng và một tiệm cận ngang.
Câu 3: Cho hàm số \(y\ =\ \frac{2x+\sqrt{x^2-4}}{x-2}\) có đồ thị (C). Chọn mệnh đề đúng trong các mệnh đề sau:
A. Đường y = 2 là một tiệm cận ngang của (C).
B. Đường y = 1 là một tiệm cận ngang của (C).
C. Đường x = - 2 là một tiệm cận đứng của (C).
D. Đường x = 3 là một tiệm cận ngang của (C).
Câu 4: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số \(y\ =\ \frac{2x-3}{\sqrt{\left(m-1x\right)x^2+4}}\) có hai tiệm cận ngang
A. m > 0
B. m ≥ 1
C. m > 1
D. Không có giá trị nào của m
Câu 5: Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu
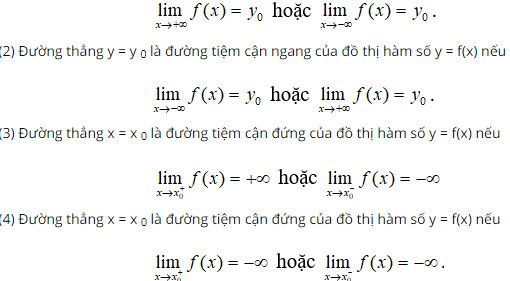
Trong các mệnh đề trên, số mệnh đề đúng là:
A.1
B. 2
C. 3
D. 4
Câu 6: Cho hàm số y = f(x) có
Trong các khẳng định dưới đây, khẳng định nào là đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 1 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 1 và x = -1
Câu 7: Tìm tất cả các giá trị thực của m để đồ thị hàm số \(y\ =\ \frac{x+1}{\sqrt{mx^2+1}}\) có hai tiệm cận ngang
A. Không tồn tại
B. m < 0
C. m = 0
D. m > 0
Câu 8: Cho hàm số \(y\ =\ \frac{3\left(x^2+1\right)\left(x\ -3\right)}{\left(x+1\right)^3}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 3 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 3 và x = -1
Câu 9: Đồ thị hàm số \(y\ =\ \frac{x+\sqrt{3}}{x+1}\) có tất cả bao nhiêu tiệm cận?
A. 0
B. 1
C. 2
D. 3
Câu 10: Hàm số nào sau đây có đồ thị nhận đường thẳng x = 0 làm tiệm cận đứng?
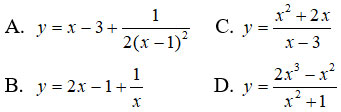
Câu 11: Đường tiệm cận ngang của đồ thị hàm số\(y\ =\ x\sqrt{x^2+2x\ }\) là:
A.y = 1
B. y = 0
C. y = -1
D. Không tồn tại
Câu 12: Đường tiệm cận đứng của đồ thị hàm số \(y\ =\ \frac{\sqrt{x}}{4-2^2}\) là:
A. x = 0
B. x = 2, x = -2
C. x - 2 = 0
D. x + 2 = 0
Câu 13: Cho hàm số \(y\ =\ \frac{mx-1}{x-m},\ m\ >1\). Hỏi giao điểm của hai đường tiệm cận của đồ thị hàm số trên luôn nằm trên một đường cố định có phương trình nào trong các phương trình sau?
A. y = x
B. x2 + y2 = 1
C. y = x2
D. y = x3
Câu 14: Đồ thị hàm số y = x3 - mx2 + 2 có tất cả bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 0
D. 3
Câu 15: Đồ thị hàm số \(y\ =\ \frac{\sqrt{x^2-x}}{x+3}\) có tất cả bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 3
D. 4
Câu 16: Đồ thị hàm số \(y\ =\ \frac{1-2x}{1-x}\) có tất cả bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải và đáp án trắc nghiệm Toán 12 chương 1
| 1-C | 2-B | 3-B | 4-C |
| 5-C | 6-B | 7-D | 8-B |
| 9-C | 10-B | 11-C | 12-C |
| 13-A | 14-C | 15-D | 16-A |
Câu 1:
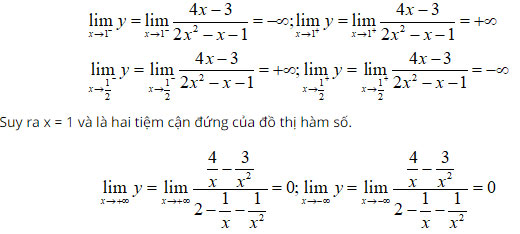
là tiệm cận ngang của đồ thị hàm số.
Chọn đáp án C
Câu 2:
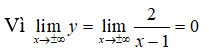
nên đồ thị hàm số có tiệm cận ngang y=0 . Chọn đáp án B.
Câu 3:
Ta có
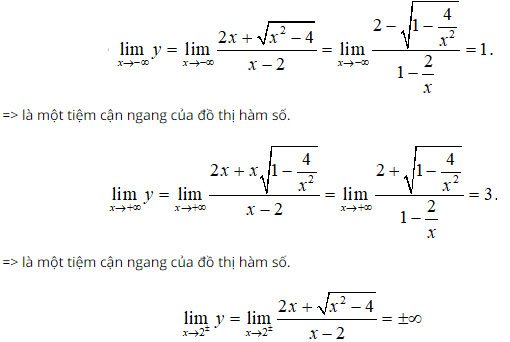
=> x = 2 là tiệm cận đứng của đồ thị hàm số.
Chọn đáp án B.
Câu 4:
Ta có
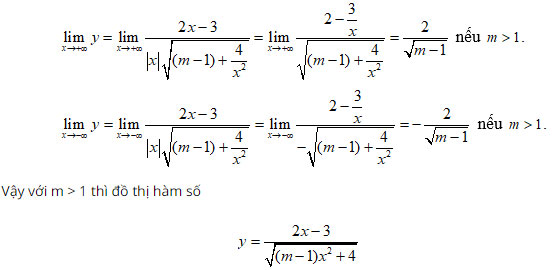
có hai tiệm cận ngang.
Chọn đáp án C.
Câu 5:
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.
Câu 6:
Từ định nghĩa đồ thị hàm số có đúng một tiệm cận ngang là y=1
Câu 7:
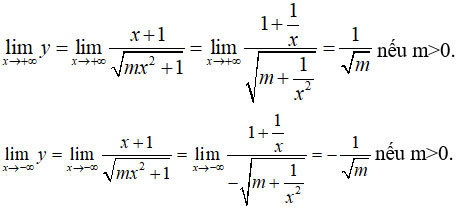
Để hàm số có hai tiệm cận ngang thì m > 0.
Câu 8:
Hàm số có đúng một tiệm cận ngang y=3.
Câu 9:
Vì x ≥ -3, nên ta chỉ xét trường hợp x → +∞
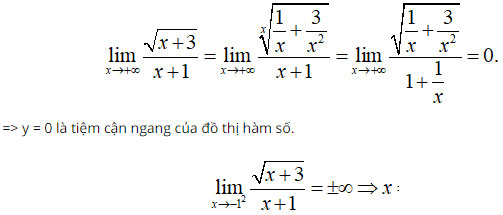
Câu 10
Câu 11:
Ta có
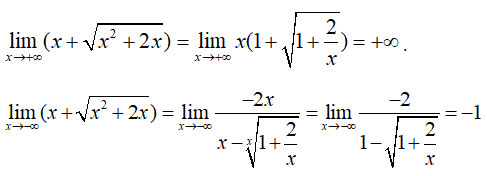
=> y= -1 là tiệm cận ngang của đồ thị hàm số.
Câu 12:
Ta có
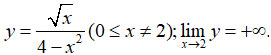
Do đó x - 2 = 0 là tiệm cận đứng của đồ thị hàm số.
Câu 13:
y = m là tiệm cận ngang, x = m là tiệm cận đứng của đồ thị hàm số. Vậy giao điểm hai tiệm cận là I(m;m). Dễ dàng nhận thấy I thuộc đường thẳng có phương trình y=x.
Câu 14:
x= -3; y=1; y= -1 là ba đường tiệm cận của đồ thị hàm số.
Câu 16:
Đồ thị hàm số có ba đường tiệm cận chỉ khi phương trình x2 -2mx + 4 = 0 có hai nghiệm phân biệt khác -1.
Trên đây VnDoc.com vừa giới thiệu tới các bạn Trắc nghiệm Toán 12 chương 1: Đường tiệm cận, mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 12. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...
Mời bạn đọc cùng tham gia nhóm Tài liệu học tập lớp 12 để có thêm tài liệu học tập nhé
